概率论与统计推断（机器学习）

统计推断（statistical inference），在计算机科学中也被称为“机器学习”，是使用数据推断生成数据分布的过程
一个经典的统计推断问题是：给一个样本(\(\sim\)意味X_1,...,X_n独立且相互都有相同的边缘分布函数，即是来自F简单随机样本)\(X_1,...,X_n \sim F\)，如何推断\(F?\)

概率论与统计推断

概率论基础

多变量分布与独立同分布样本

令\(X=(X_1,...X_n)\)，其中\(X_1,...X_n\)均为随机变量。这时，我们称\(X\)为一个随机向量(random vector)。
如果\(X_1,...,X_n\)独立且相互都有相同的边缘分布函数\(F\)，我们称\(X_1,...X_n\)是独立同分布(IID, independent and identically distributed)的，同时使用如下记号表示：

\[X_1,...,X_n \sim F \]

如果分布\(F\)有密度函数\(f\)我们也写作\(X_1,...,X_n \sim f\)。我们也称\(X_1,...,X_n\)是来自\(F\)的大小为\(n\)的随机样本（注，国内一般称之为简单随机样本）。

此时由于独立性，

\[P(X_1\in A_1, ..., X_n\in A_n) = \prod_{i=1}^{n} P(X_i\in A_i)，等价于f(x_1,...,x_n)=\prod_{i=1}^{n} f_{X_i}(x_i) \]

独立同分布(IID, independent and identically distributed)样本具有相互独立且相同的多变量分布。
大部分统计推断理论和应用都是以独立同分布(IID)观测量为基础的。

Chernoff Bound

一个可能的解释：Hoeffding 不等式是 Chernoff 界的推广，后者适用于 Bernoulli 随机变量，主要用于学习理论中(基于Wikipedia)。
另一个可能的解释：在学习理论(learning theory)中被称为Chernoff Bound，两者等价(基于CMU Eric Xing的ppt)
这两者的关系有一定考究的价值，在此不详谈

Chernoff 界在计算学习理论中用于证明学习算法可能近似正确，即该算法在足够大的训练数据集上具有很小的误差的概率很高。因为其定义使用了独立同分布样本。

矩母函数(Moment Generating Function)

\(e^x\)的麦克劳林公式定义为

\[e^x = \sum_{n=0}^{\infty}\frac{x^n}{n!} \]

关于随机变量X的矩母函数，或者拉普拉斯变换，被定义为

\[M_X(t) = E(e^{tX}) = \int e^{tx}dF(x) \]

t的取值范围为实数。

对t求导，从而可知

\[M_X^{(n)}(0) = E(e^{tX})^{(n)}|_{t=0} = E(X^ne^{{(tX)}^n})|_{t=0} = E(X^n) \]

此处t取0.这是用导数方法的的出来的结论。而将\(e^x\)化为泰勒级数，可得

\[M_X^{(n)}(0) = E(e^{tX})^{(n)}|_{t=0} = E(\sum_{n=0}^{\infty}\frac{{(tX)}^n}{n!})^{(n)}|_{t=0} = E(X^n) \]

有同样结果。拉普拉斯变换最玄妙之处在于其与泰勒级数的关系。

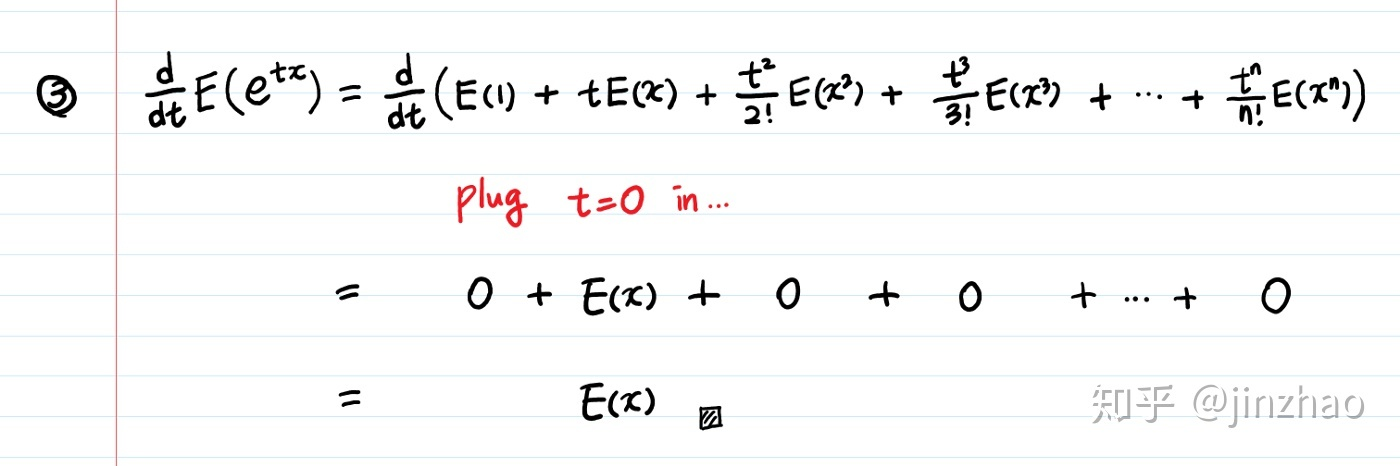
只有在项中存在为\({t^n}\)才能n次求导到非0项，过大因为t=0的缘故亦为0.

马尔可夫不等式（Markov's inequality）

令X是一个非负随机变量并且E(X)存在，则对于任意t>0，有

\[P(X>t) \le \frac{E(X)}{t} \]

证明：
因为随机变量X>0，

\[E(X) = \int_{0}^{\infty}xf(x)dx = \int_{0}^{t}xf(x)dx + \int_{t}^{\infty}xf(x)dx \ge \int_{t}^{\infty}xf(x)dx \ge t\int_{t}^{\infty}f(x)dx = tP(X>t) \]

切比雪夫不等式（Chebyshev's inequality）

证明：
使用马尔可夫不等式:

\[P(|X-\mu| \ge t) = P({|X-\mu|}^2 \ge t^2) \le \frac{E(X-\mu)^2}{t^2} = \frac{\sigma^2}{t^2} \]

霍夫丁不等式（Hoeffding's inequality），切尔诺夫界(Chernoff bound)

霍夫丁不等式与马尔可夫不等式有共通之处，但霍夫丁不等式是一个更sharper的不等式。
\(\epsilon\)为常值epsilon符号。
霍夫丁不等式：

\[令Y_1,...,Y_n是独立观测值，使得E(Y_i)=0且a_i \le Y_i \le b_i.令\epsilon > 0, 那么，对任意t>0: \]

\[P(\sum_{i=1}^{n}Y_i \ge \epsilon) \le e^{-t\epsilon}\prod_{i=1}^{n}e^{t^2{(b_i-a_i)}^2/8} \]

另一个结论：

\[令X_1,...,X_n \sim B(p).那么, 对任意\epsilon > 0, \]

\[P(|\overline{X}_n-p|>\epsilon) \le 2e^{-2n{\epsilon}^2} \]

\[这里\overline{X}_n=\frac{\sum_{i=1}^{n}X_i}{n} \]

例子

令\(X_1,...,X_n \sim B(p)\)，即是来自\(B(p)\)的简单随机样本.令\(n=100\)且\(\epsilon=0.2\)。

我们使用切比雪夫不等式做第一次估计，因为切比雪夫本质上是Markov的变形，且使用方差而不是期望的性质，使得可以用于\(B(p)\)的估计。

\[P(|\overline{X}_n-p|>0.2) \le \frac{p(1-p)}{n{\epsilon}^2} \le \frac{1}{4n{\epsilon}^2} = 0.0625 \]

\[P(|\overline{X}_n-p|>0.2) \le 2e^{-2(100)(0.2^2)} = 0.00067 \]

可见，霍夫丁不等式更加sharper，n不断增大，霍夫丁不等式的减小速率更快且具有通用性。

证明
矩母函数的两个定理

\(Theorem 4.2:\)
令X和Y为两个随机变量，如果

\[M_X(t)=M_Y(t) \]

在所有\(t \in (-\delta, \delta)(\delta > 0)\)上都成立，那么\(X\)和\(Y\)具有相同的分布。

\(Theorem 4.3:\)
令X和Y为两个独立随机变量，那么\(M_{X+Y}(t)=M_X(t)M_Y(t)\).

证明:
\(M_{X+Y}(t)=E[e^{t(X+Y)}]=E[e^{tX}e^{tY}]=E[e^{tX}]E[e^{tY}]=M_X(t)M_Y(t)\)
\(由于独立性，可得E[e^{tX}e^{tY}]=E[e^{tX}]E[e^{tY}]\)

切尔诺夫界的证明

应用Markov不等式：
对于任意\(t>0\)，

\[P(X \ge a) = P(e^{tX} \ge e^{ta}) \le \frac{E[e^{tX}]}{e^{ta}} \]

特别地，

\[P(X \ge a) \le \min_{t>0}\frac{E[e^{tX}]}{e^{ta}} \]

相似地有对任意\(t<0\)，

\[P(X \ge a) \le \min_{t<0}\frac{E[e^{tX}]}{e^{ta}} \]

关键是最小化\(\frac{E[e^{tX}]}{e^{ta}}\)的\(t\)值。

Partial Reference

ChangeLog

  • 11月01日 19:38 写了第一部分。
  • 11月03日 22:00 补充Reference和前面的部分。有一点困明天再写。明天要写Chernoff界相关内容，不可避免引入Markov不等式等概念。
  • 11月07日 21:32 后面继续补充霍夫丁不等式和数理统计内容。有时间再写吧。
  • 11月08日 19:51 书不在旁边明天再写吧。
  • 11月12日 16:39 霍夫丁不等式补充了一点。晚上写完这部分。
  • 12月1日 15:42 切尔诺夫界需要继续补充。等我仔细研读后再写。估计要将所有分布的属性要解释一遍。
posted @ 2021-11-01 20:10  千心  阅读(491)  评论(0)  编辑  收藏  举报