《深度学习与Pytorch入门实战》2019
《深度学习与Pytorch入门实战》2019
其他
https://www.cnblogs.com/taosiyu/category/1538754.html
1-深度学习框架简介
- pytorch动态图:

一步一步给定数据计算,随时查看每一步数据,较符合人的思维逻辑。
TensorFlow静态图:

先define定义阶段,再run,函数给出xy的值及输出。
2-
3-开发环境安装


右键,管理员身份运行
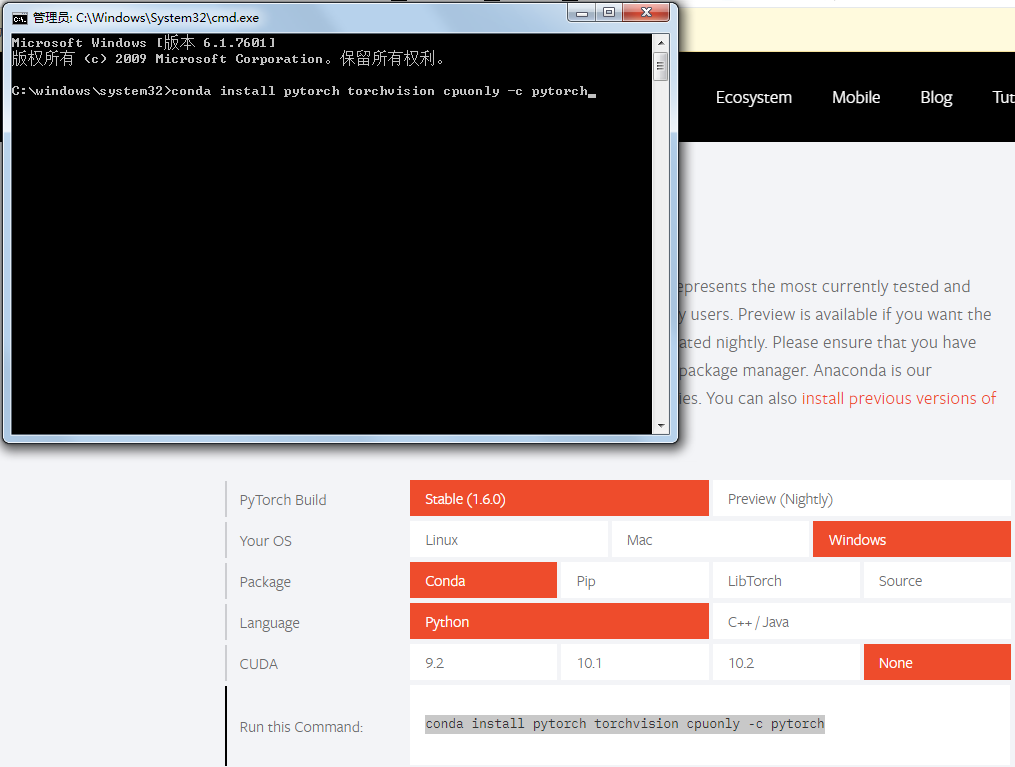
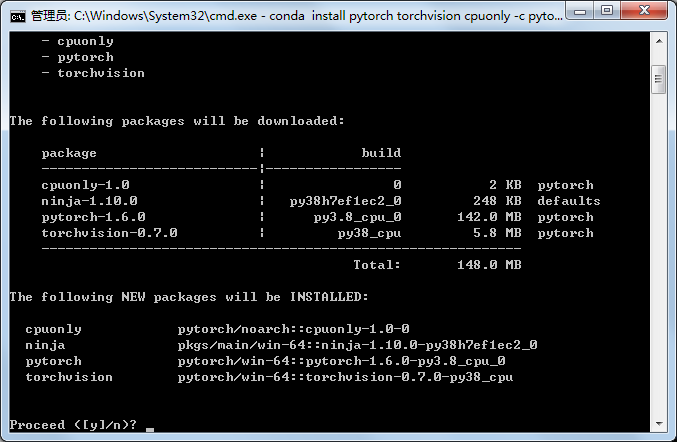
4、5-简单回归问题
- 梯度下降算法
loss=x^2*sinx
新的x: x'=x-learning rate*y'(x)
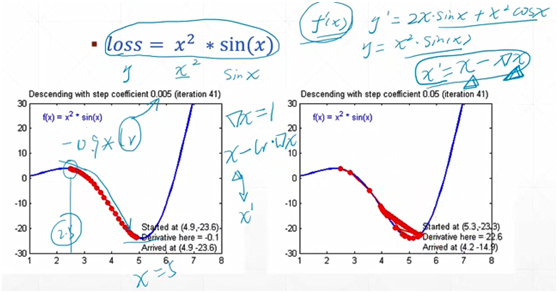
因为有误差,在理论的最优解(x=5)附近有一定程度的抖动

learning rate设成0.05以后,步长变大,波动程度较大,效果不好
learning rate一般设定为0.001,简单的可以设成0.01等等
y=w*x+b+∈
噪声 ∈~N(0.01,1)
min loss=∑_i〖(w*x_i+b-y_i)〗^2
w'*x+b'→y
6-回归问题实战
points是一系列x、y的数据点。如下图红点
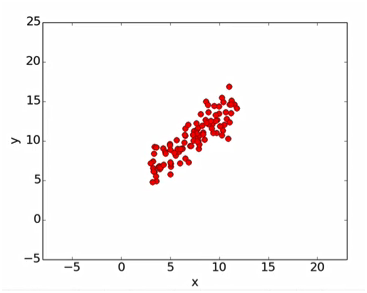
- 求loss:
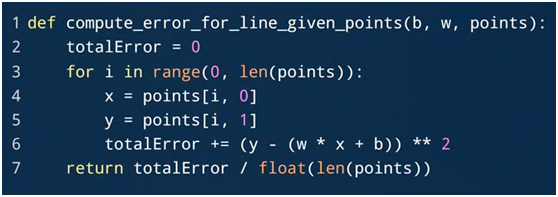
python range()函数可创建一个整数列表:
range(start, stop[, step])
start:计数从 start 开始。默认从 0 开始。
stop:计数到 stop 结束,但不包括 stop。
step:步长,默认为1。
- 求梯度信息w、b:

11、12行的m应改为w
除以N是为了累加后的求average。

- 迭代优化:

7-8-分类问题引入
- ReLU:线性整流函数,又称修正线性单元,是一种非线性函数。


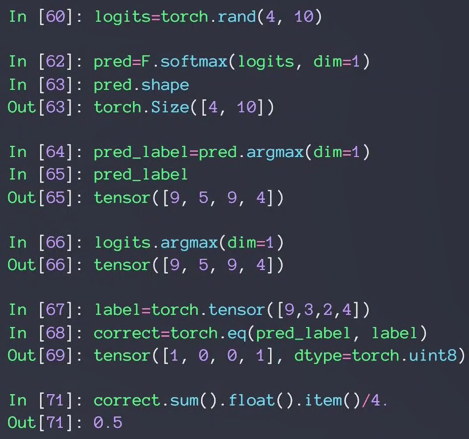
最大值0.8所在的索引为1

label为1的概率为0.8

argmax也就是label
9-13-手写数字识别初体验
14-15-张量数据类型
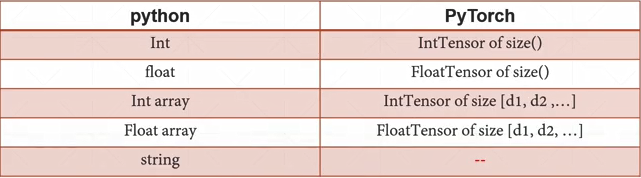
- 没有内建String支持,必须使用编码的方式:
1.one-hot code:如[0100000]

无法体现单词间的相关性,如like dislike
2.embedding:如Word2vec、glove
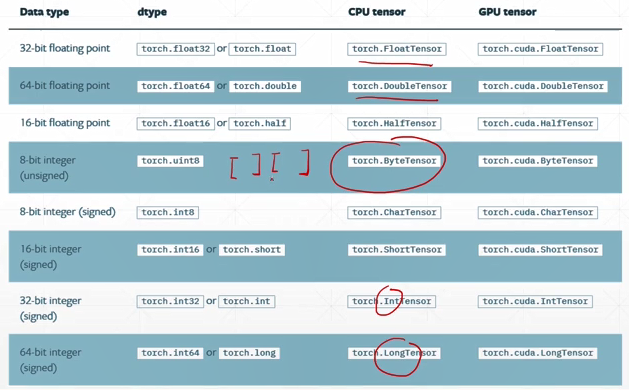
ByteTensor,判断两Tensor元素是否相等,返回0或1
部署在CPU GPU上是不一样的
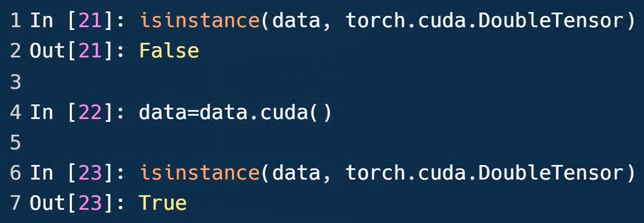
x.cuda会返回一个GPU上的引用
- 三种Tensor类型的判断方法
随机初始化一个两行三列的二维的Tensor,randn随机正态分布的数中选取
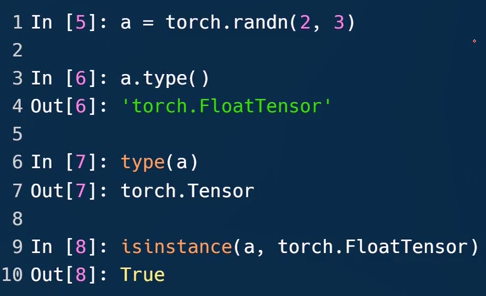
第一种打印出具体数据类型;第三种判断是否是某种类型,是返回true
- 标量 Dimension=0
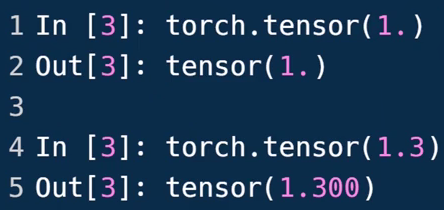
1.3是0维,但[1.3]是1维长度为1的Tensor
获取标量的shape

len(a.dim)也会返回0
- Dim=1的张量/向量
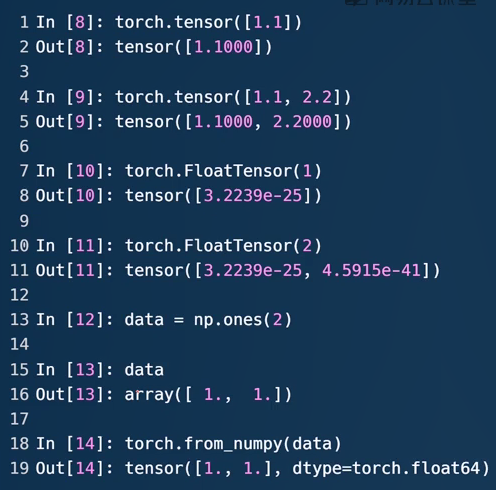
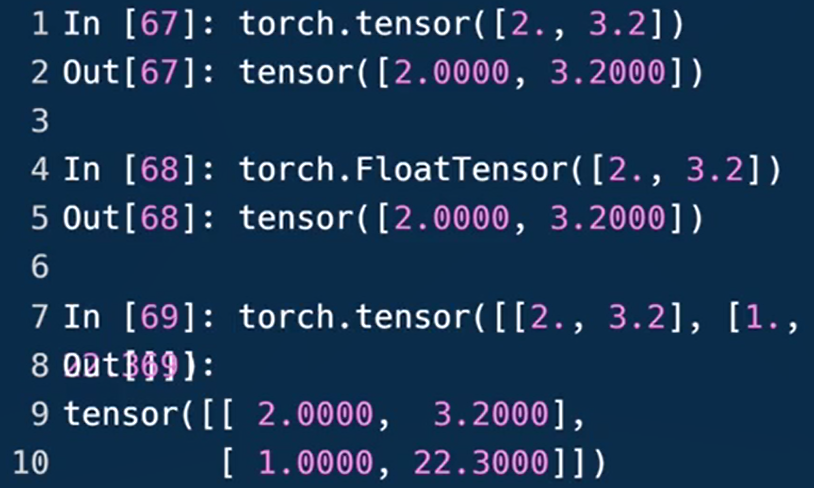
.tensor接受的是数据的内容,后接现有的数据
.FloatTensor接受的是数据的shape,也可接受现有的数据但容易混淆故不推荐。第7行给定向量的长度为1,8行随机初始化一个数值。
13行从numpy引入,规定长度为2。生成[1.,1.](16行)
18行使用form_numpy方法从data里引入,显示数据一样,但类型变成FloatTensor
应用:Bias偏置;Linear Input神经网络线性层的输入
- Dim=2的张量
获取shape(size):
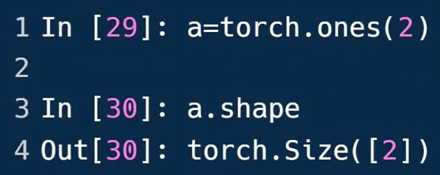
区分:
dim:2
size/shape:[2,2]
tensor:[1 2]
[3 4]
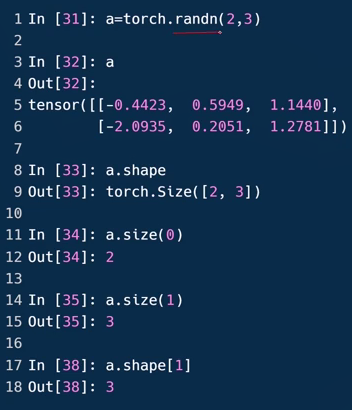
a.size不给参数返回第9行
应用:带有batch的Linear Input
- Dim=3的张量
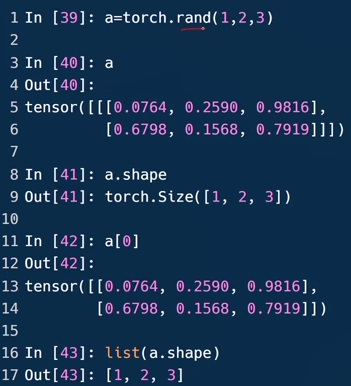
.rand [0,1)随机的均匀分布中的数据来初始化
第一个维度是1,所以第5行在一个总的括号[]内;第二个维度是2,所以第二个[]内两个元素;…
应用:带有batch的RNN Input
- Dim=4
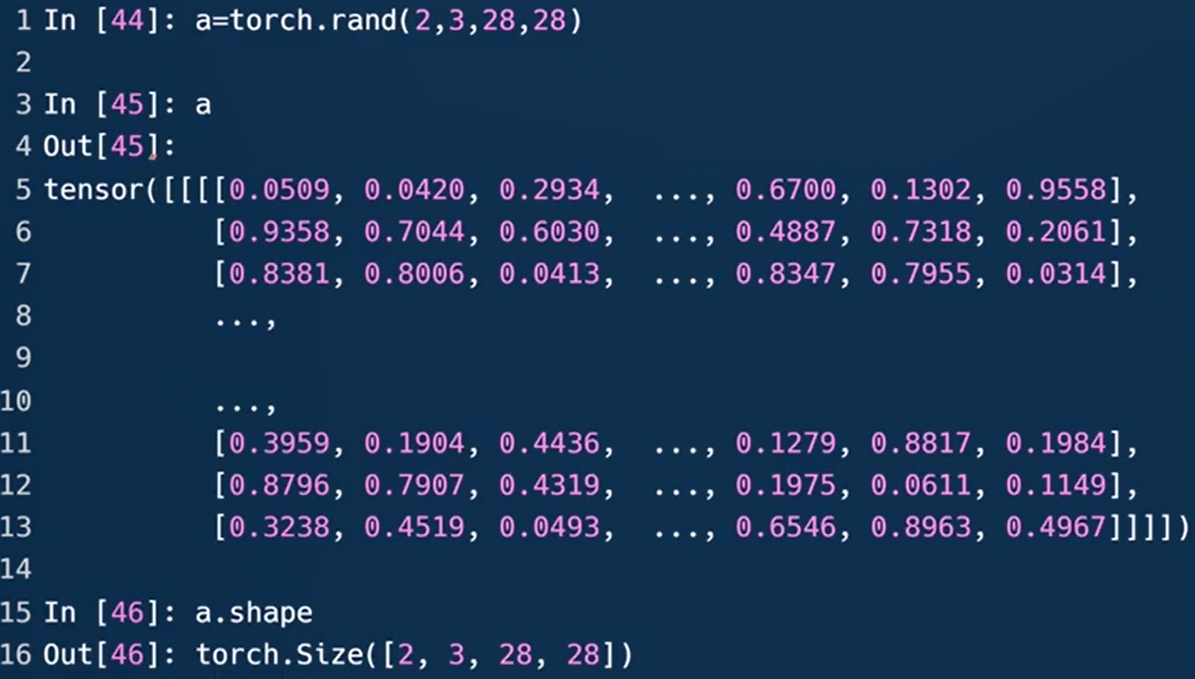
可用于表示图片
图中第一个维度2,表示照片数b为2;第二个维度3,灰度图的通道数channel为1,彩色图通道数为3;第三四个维度18是MNIST数据集的长h和宽w。
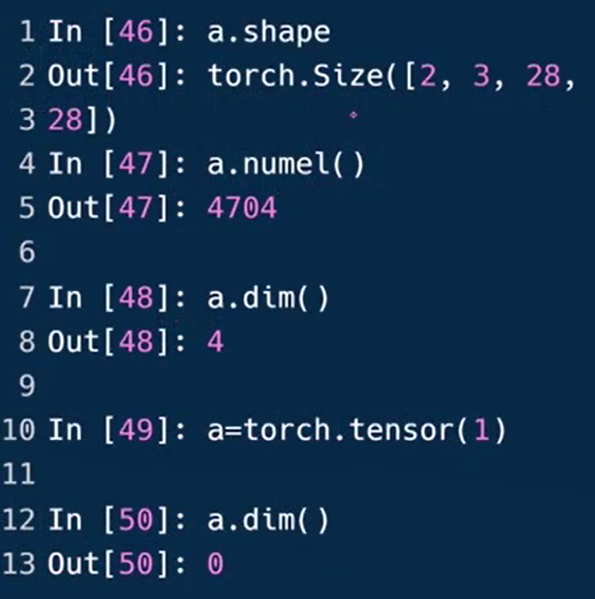
munel指tensor占用内存的数量
16-17-创建tensor
- 从numpy引入

通过numoy创建一个dim=1,长度为2的向量
从numpy导入的float其实是double类型
- 通过list方法导入
- 生成未初始化的数据
·torch.enpyt()
·torch.FloatTensor(d1,d2,d3)
NOT torch.FloatTensor([1,2])=torch.tensor([1,2])
·torch.IntTensor(d1,d2,d3)
未初始化的tensor一定要跟写入数据的后续步骤
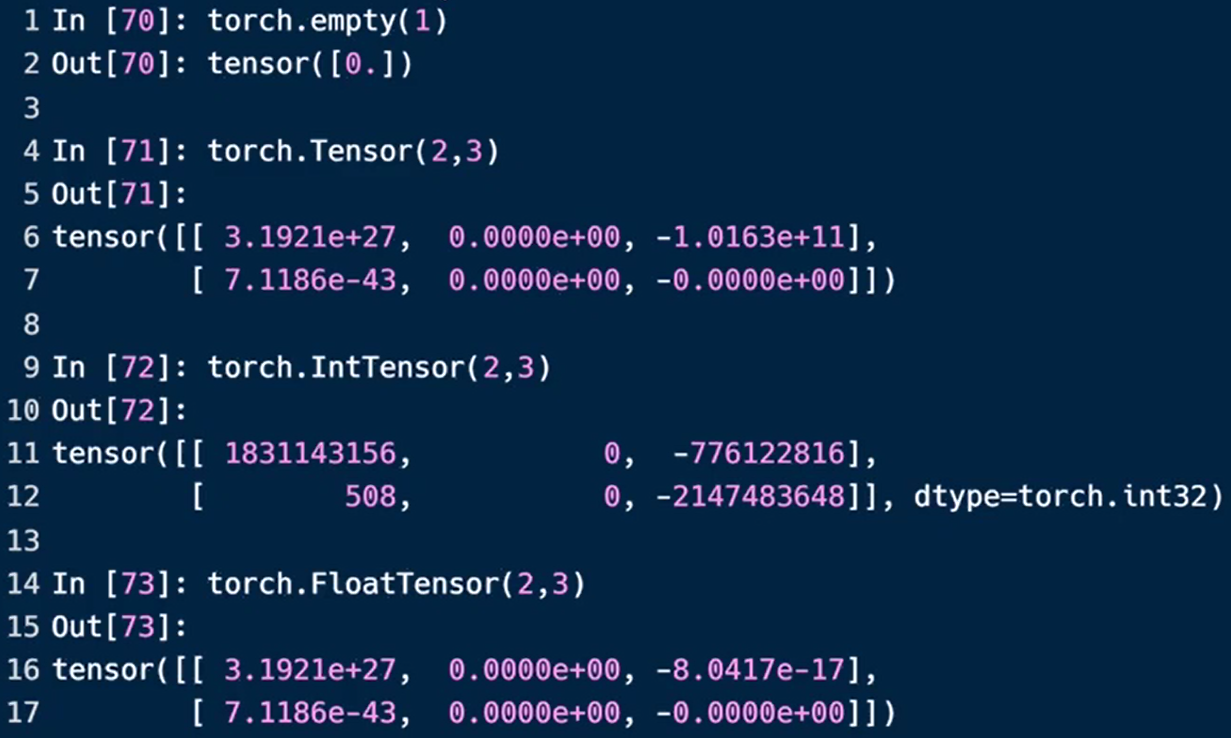
第二行的0是随机出来的巧合

pytorch里.tensor默认类型是FloatTensor,torch.set_default_tensor_type()可修改默认类型(第四行)
增强学习里一般使用double,其他一般使用float
- 随机初始化
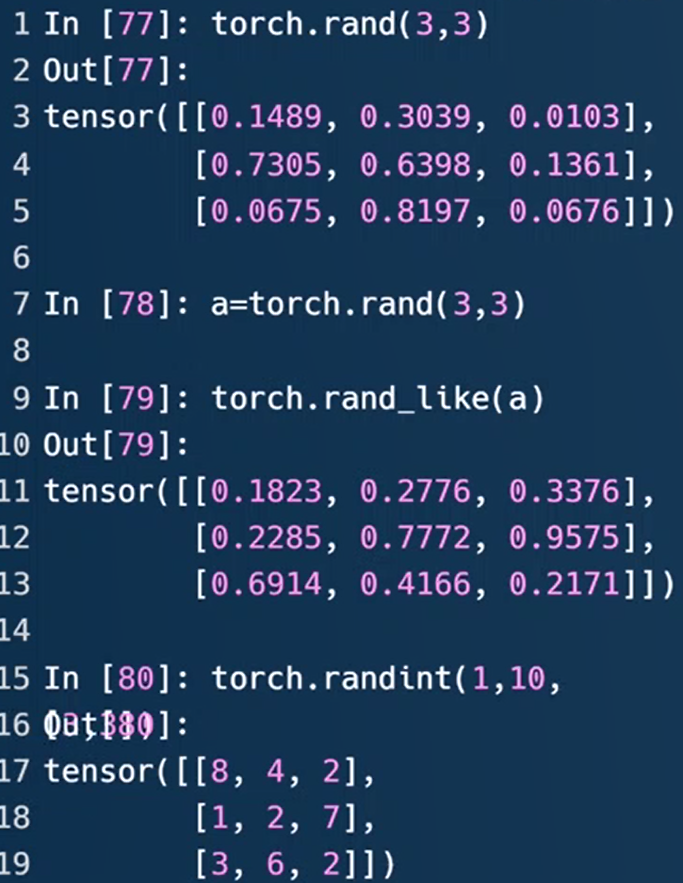
重叠部分为[3.3])
rand随机产生0-1之间的数值,不包括1。也就是[0,1)均匀分布
rand_like()接受的参数不再是shape,而是tensor
randint(min,max,[维度,…])采样[min,max)间的整数值
均匀采样0-10的tensor要用x=10*torch.rand(d1,d2)

randn,初始化时的随机数服从正态分布,最常见的是N(0,1)
torch.normal(means, std, out=None)返回一个张量,包含从给定参数means为均值,std为标准差的离散正态分布中抽取随机数。out为可选的输出张量。
torch.full([],?)依size生成值均为?的元素的张量。size:张量的形状,如[3,3]、[10]。图中为生成10个0:[0,0,0,…,0]
torch.arange(start,end,step)start:数列起始值,end:数列“结束值”(取不到),step:数列公差,默认为1。图中为[1,0.9,0.8,……,0.1]
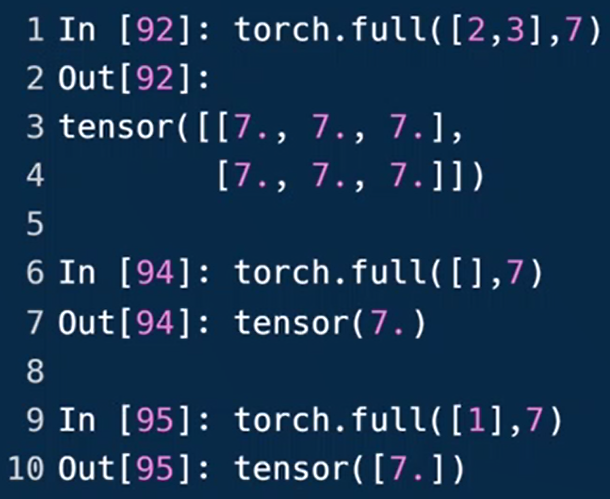
例94生成Dim=0的标量,95生成Dim=1,长度为1的张量

例98方法不建议
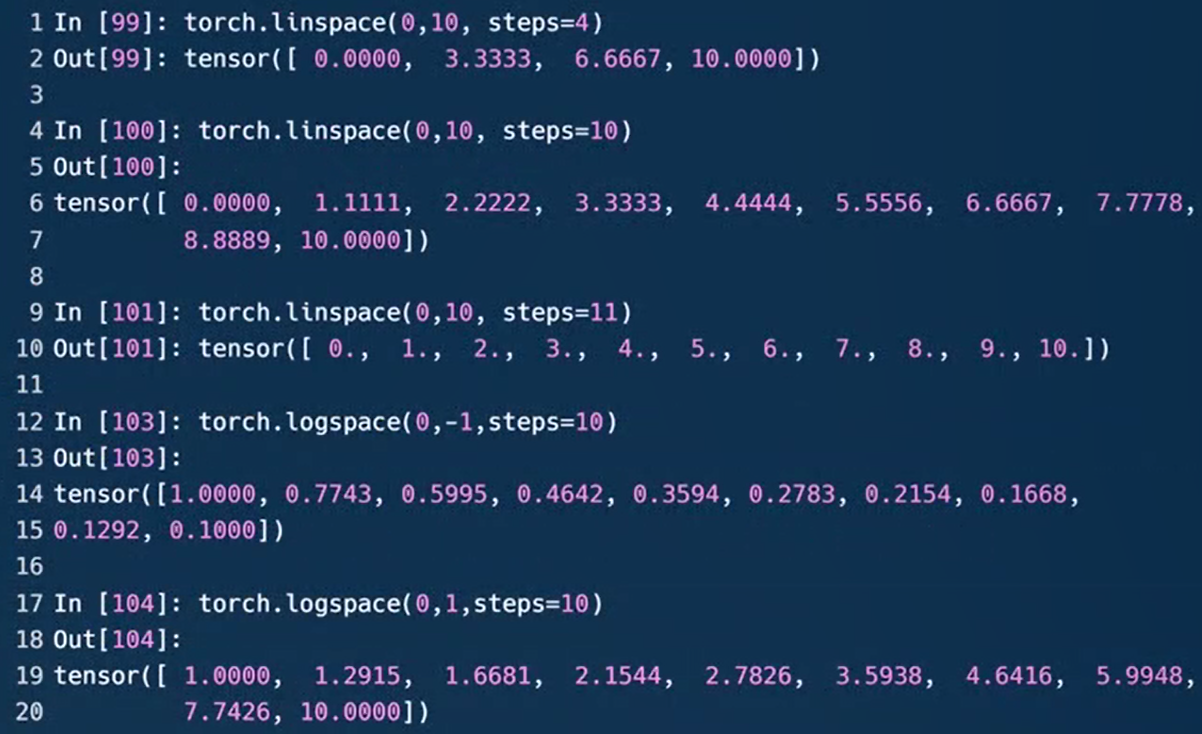
torch.linspace(start, end, steps=?)线性等分向量。start:开始值,end:结束值(能取到),steps:在start和end间生成的样本数,默认是100。
torch.logspace(start, end, steps=100)返回一个1维张量,包含在区间10(start)和10(end)(能取到)上以对数刻度均匀间隔的 steps个点。

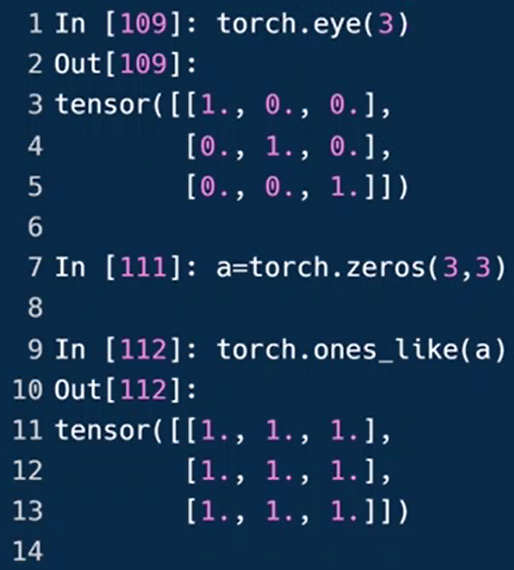
torch.ones(size)返回一个全为1的张量,形状由可变参数sizes定义
torch.zeros(size)返回一个全为标量0的张量,形状由可变参数sizes定义
torch.eye(n, m)返回一个2维张量,对角线为1,其它位置为0。n-行数;m-列数,默认为n
torch.randperm(n)返回一个从0到n-1的随机整数排列


用同一个索引来做shuffle,比如a为人名+数学成绩,b为人名+语文成绩,索引要对应起来。
4-7是为了演示得到了不同的idx,第9、14行的idx必须保持一致
18-19-索引与切片
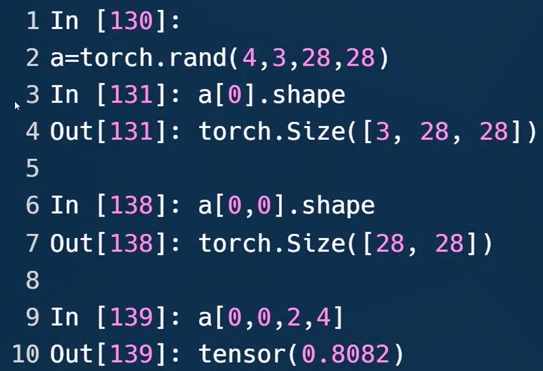
a[0],取第=张图片,包含3个通道,长宽各为28。
a[0,0,2,4],第0张图片,第0个通道,第2行第4列的像素点
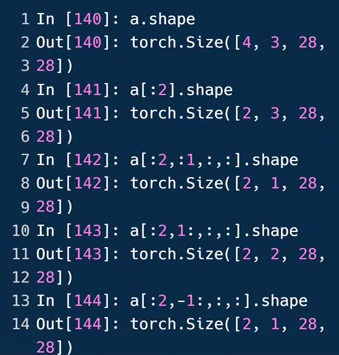
start:end:step
:2可理解为→2,从最开始(第0张)的图片到第二张图片(不包含第二张)。不写数字默认取全部。
例143中,1:表示从第一个通道开始取到最末尾,也就是G、B两通道
例144中,反向索引,-1:也就是最后一个元素开始取,也就是B通道
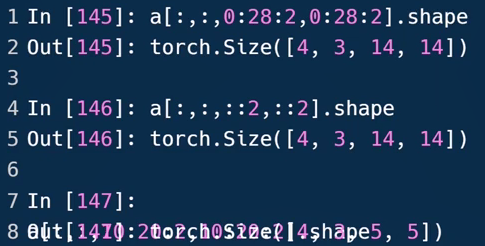
0:28:2隔行采样,对序号0至序号28(取不到)进行间隔采样,每隔2采一次,也就是采序号为0,2,4,6,...,26的元素,共14个
0:28:等同于0:28:1
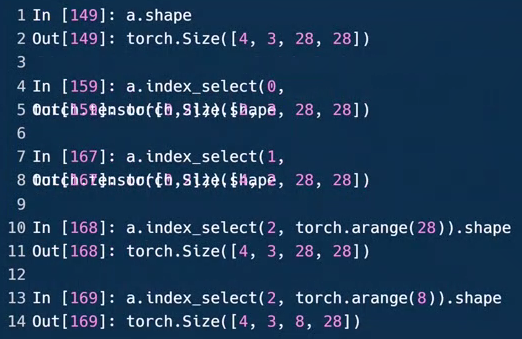
第4行:a.index_select(0,torch.tensor([0,2])).shape
第5行:[2,3,28,28]
index_select(dim,index)dim:表示从第几维挑选数据;index:表示从第一个参数维度中的哪个位置挑选数据,类型为torch.Tensor类的实例
第7行:a.index_select(1,torch.tensor([1,2])).shape
第8行:[4,2,28,28]
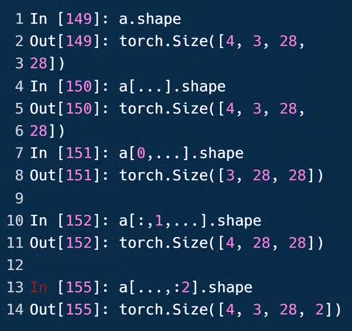
...表示任意多的维度
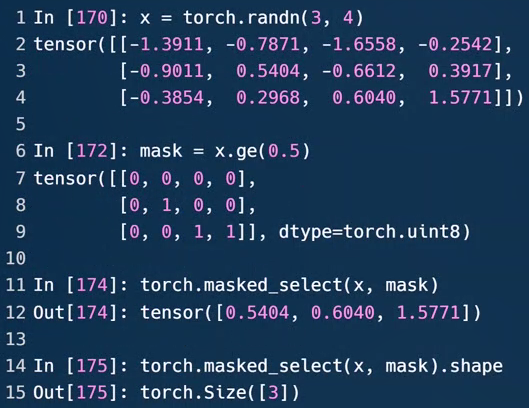
.gt() #greater than(大于)
.ge() #greater and equal(大于等于)
.eq() #equal(等于)
.le() #less and equal(小于等于)
.lt() #less than(小于)
第6行,大于等于0.5的数置为1,否则置为0
torch.masked_select(input, mask)。input输入张量,mask掩码张量。mask须跟input有相同数量的元素数目,但形状或维度不需要相同。
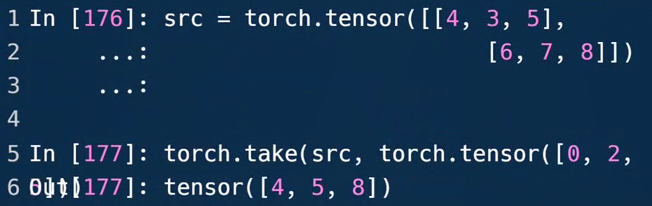
In[39]: src = torch.tensor([[4,3,5],[6,7,8]]) # 先打平成1维的,共6列
In[40]: src
Out[40]:
tensor([[4, 3, 5],
[6, 7, 8]])
In[41]: torch.take(src, torch.tensor([0, 2, 5])) # 取打平后编码,位置为0 2 5
Out[41]: tensor([4, 5, 8])
torch.take(src, torch.tensor([index]))打平后,按照index来取对应位置的元素
20-23-维度变换
tensor的维度变化改变的是数据的理解方式
.view()/.reshape():返回的数据和传入的tensor一样的条件下,转变shape

第4行:(4,12828)将通道、长宽合并,忽略了通道信息、上下左右的空间信息。适合全连接层。
保证tensor的size不变即可/numel()一致/元素个数不变。
view操作必须满足物理意义,否则会导致数据的被污染与破坏
第16行:合并batch、channel、行,放在一起为N,[N,28],每个N,刚好有28个像素点,只关心一行数据
第19行:4张叠起来了
损失维度信息,如果不额外存储维度顺序的话,恢复时会出现问题。如22-24行的逻辑混乱。
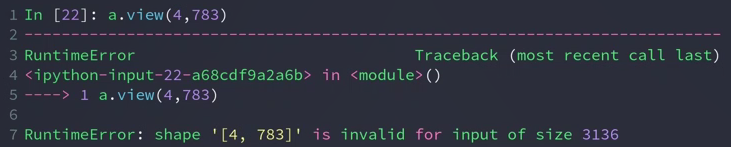
view的新的size(783)与原来(784)不一致会报错
squeeze/unsqueeze:减少/增加维度
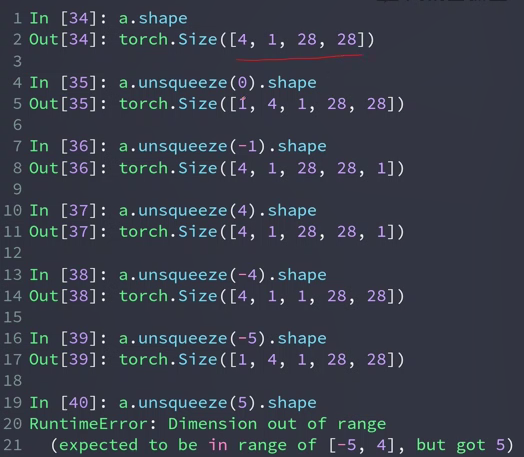
unsqueeze(index) 拉伸(增加一个维度/一个组,而非一个数据,还是4张图片,可以理解为增加了一个组,组里有原来的四张图片)
参数的范围是 [-a.dim()-1, a.dim()+1) 如图中例子中范围是[-5,5)
-5→0,…,-1→4 这样的话,0表示在前面插入,-1表示在后面插入,正负会有些混乱,所以推荐用正数。
| [ | 4 | 1 | 28 | 28 | ] |
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| -5 | -4 | -3 | -2 | -1 |
0与正数,就是在第X个维度前面插入,负数在某个维度后面插入
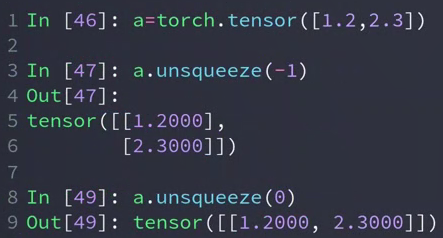
In[24]: a = torch.tensor([1.2,2.3]) # 维度为[2]
In[27]: a.shape
Out[27]: torch.Size([2])
In[25]: a.unsqueeze(-1) # -1,后面增加维度,维度变成[2,1] 2行1列
Out[25]:
tensor([[1.2000],
[2.3000]])
In[26]: a.unsqueeze(0)
Out[26]: tensor([[1.2000, 2.3000]]) # 0,前面增加维度,维度变成[1,2] 1行2列
- 实例
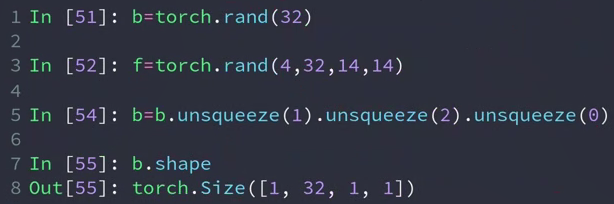
给一个bias(偏置),bias相当于给每个channel上的所有像素增加一个偏置
为了做到 f+b 我们需要改变b的维度

squeeze(index)当index对应的dim为1,才产生作用。例64中第1个维度32≠1,不能挤压。
不写参数,会挤压所有维度为1的。例61将所有维度为1的进行挤压,理解:一张图片,有32个channel,每个channel有一个点(值)
expand/repeat:维度扩展
Expand:broadcasting(推荐),只是改变了理解方式,并没有增加数据。只在需要的时候复制数据,不会主动复制。速度快节约内存。
Reapeat:memory copied,会实实在在的增加数据
以上面提到的实例为例, b[1,32,1,1]与f[4,32,14,14],目标是将b的维度变成与f相同的维度(1→4,1→14,1→14)。
- 扩展(expand)张量不会分配新的内存,只是在存在的张量上创建一个新的视图(view)
In[44]: a = torch.rand(4,32,14,14)
In[45]: b.shape
Out[45]: torch.Size([1, 32, 1, 1]) # 只有1→N才是可行的, 3→N需要另起规则
In[46]: b.expand(4,32,14,14).shape
Out[46]: torch.Size([4, 32, 14, 14])
In[47]: b.expand(-1,32,-1,-1).shape # -1表示这个维度不变
Out[47]: torch.Size([1, 32, 1, 1])
In[48]: b.expand(-1,32,-1,-4).shape # -4这里是一个bug,没有意义,最新版已经修复了
Out[48]: torch.Size([1, 32, 1, -4])
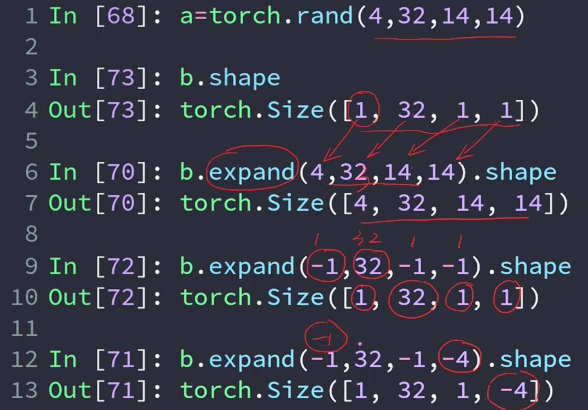
- repeat:
主动复制原来的。
参数表示的是要拷贝的次数/是原来维度的倍数
沿着特定的维度重复这个张量,和expand()不同的是,这个函数拷贝张量的数据。

t/transpose/permute:转置,单次/多次交换
- .t
a = torch.randn(3,4)
a.t().shape
Out[58]: torch.Size([4, 3])
In[60]: a
Out[60]:
tensor([[ 0.5629, -0.5085, -0.3371, 1.2387],
[ 0.2142, -1.7846, 0.2297, 1.7797],
[-0.3197, 0.6116, 0.3791, 0.9218]])
In[61]: a.t()
Out[61]:
tensor([[ 0.5629, 0.2142, -0.3197],
[-0.5085, -1.7846, 0.6116],
[-0.3371, 0.2297, 0.3791],
[ 1.2387, 1.7797, 0.9218]])
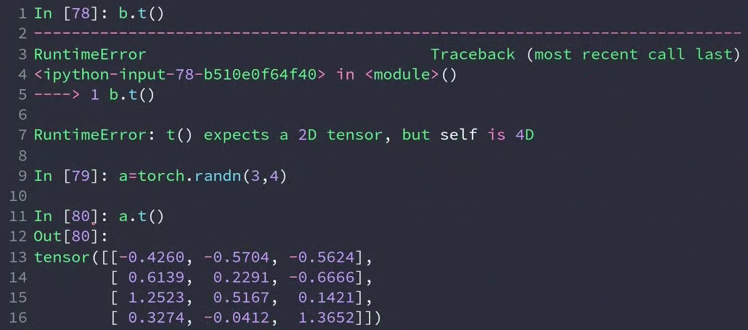
b.t()
RuntimeError: t() expects a tensor with <= 2 dimensions, but self is 4D
.t 只针对2维矩阵
- transpose
在结合view使用的时候,view会导致维度顺序关系变模糊,所以需要人为跟踪。
错误的顺序,会导致数据污染
一次只能两两交换
In[8]: a = torch.randn(4,3,32,32)
In[9]: a.shape
Out[9]: torch.Size([4, 3, 32, 32])
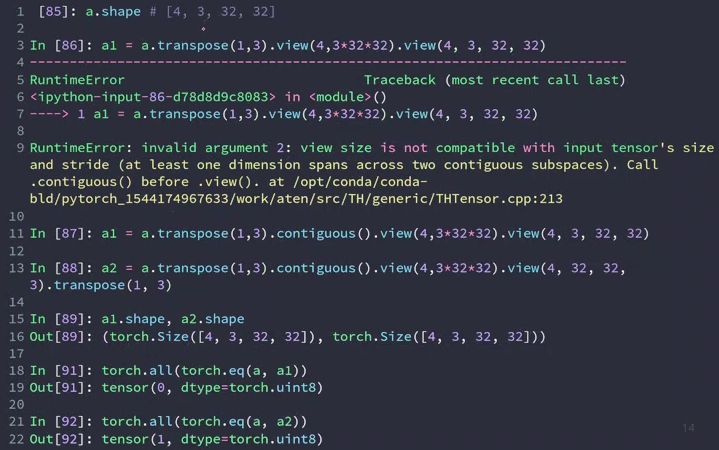
In[10]: a1 = a.transpose(1,3).contiguous().view(4,3*32*32).view(4,3,32,32)
# 由于交换了1、3维度,就会变得不连续,所以需要用contiguous,来把数据变得连续。
# [b c h w]交换1、3维度的数据变成[b w h c],再把后面的三个连在一起,展开后变为[b c w h],导致和原来的顺序不同,造成数据污染
In[11]: a1.shape
Out[11]: torch.Size([4, 3, 32, 32])
In[12]: a2 = a.transpose(1,3).contiguous().view(4,3*32*32).view(4,32,32,3).transpose(1,3)
# [b c h w] -> [b w h c] -> [b w h c] -> [b c h w] 和原来顺序相同。
In[13]: a2.shape
Out[13]: torch.Size([4, 3, 32, 32])
# 验证向量一致性
In[14]: torch.all(torch.eq(a,a1)) # 使用.eq函数比较数据是否一致,.all函数保证每一处数据都一致
Out[14]: tensor(0, dtype=torch.uint8)
In[15]: torch.all(torch.eq(a,a2))
Out[15]: tensor(1, dtype=torch.uint8)
tensor.all()功能: 如果张量tensor中所有元素都是True, 才返回True; 否则返回False
torch.all() 判断每个位置是否存在为0的元素
In[21]: torch.all(torch.ByteTensor([1,1,1,1]))
Out[21]: tensor(1, dtype=torch.uint8)
In[22]: torch.all(torch.ByteTensor([1,1,1,0]))
Out[22]: tensor(0, dtype=torch.uint8)
tensor.any()功能: 如果张量tensor中存在一个元素为True, 那么返回True; 只有所有元素都是False时才返回False
- permute
permute会打乱内存顺序,也需要contiguous

In[18]: a = torch.rand(4,3,28,28)
In[19]: a.transpose(1,3).shape
# [b c h w] → [b w h c], h与w的顺序发生了变换,导致图像发生了变化
Out[19]: torch.Size([4, 28, 28, 3])
In[20]: b = torch.rand(4,3,28,32)
In[21]: b.transpose(1,3).shape
Out[21]: torch.Size([4, 32, 28, 3])
In[22]: b.transpose(1,3).transpose(1,2).shape
Out[22]: torch.Size([4, 28, 32, 3])
# [b,h,w,c]是numpy存储图片的格式,需要这一步才能导出numpy
In[23]: b.permute(0,2,3,1).shape
Out[23]: torch.Size([4, 28, 32, 3])
24-26-broadcast
- 自动扩展:
维度扩展,自动调用expand
without copying data ,不需要拷贝数据。
- 实施
从最小的维度开始匹配,前面没有维度的话,在前面插入一个维度;然后将size 1扩展成相同size的维度
例子:对于 feature maps : [4, 32, 14, 14],想给它添加一个偏置Bias
Bias:[32] –> [32, 1 , 1] (手动插入两个维度以满足broadcast的条件) => [1, 32, 1, 1] => [4, 32, 14, 14]
目标:当Bias和feature maps的size一样时,才能执行叠加操作
- Broadcast的原因
broadcast = unsqueze(插入新维度) + expand(将1dim变成相同维度)

- 实例
有这样的数据 [class, students, scores],具体是4个班,每个班32人,每人8门课程[4, 32, 8] 。
考试不理想,对于这组数据我们需要为每一位同学的成绩加5分
要求: [4, 32, 8] + [4, 32, 8]
实际上:[4, 32, 8] + [5.0]
操作上:[1] =>(unsqueeze) [1, 1, 1] =>(expand_as) [4, 32, 8],这样需要写3个接口。所以需要broadcast
内存:
[4, 32, 8] => 1024
[5.0] => 1 如果是手动复制的话,内存消耗将变为原来的1024倍
- 使用条件
A [ 大维度 —> 小维度 ]
从最后一位(最小维度)开始匹配,如果维度上的size是0,1或相同,则满足条件,看下一个维度,直到都满足条件为止。
如果当前维度是1,扩张到相同维度
如果没有维度,插入一个维度并扩张到相同维度
当最小维度不匹配的时候没法使用broadcastiong,如共有8门课程,但只给了4门课程的变化,这样就会产生歧义。
小维度指定,大维度随意
小维度指定:假如英语考难了,只加英语成绩 [0 0 5 0 0 0 0 0]
- 具体案例分析
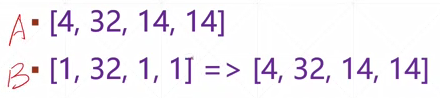
size一样,不需要扩展,只扩张到相同维度即可

先增加维度,再扩张

B只给了两张照片的参数,不符合要求
- 使用
A [4, 3, 32, 32] b,c,h,w
+[32, 32] 叠加一个相同的feature map,做一些平移变换。相当于一个base(基底),
+[3, 1, 1] 针对 RGB 进行不同的补充,如R 0.5 、G 0 、B 0.3
+[1, 1, 1, 1] 对于所有的都加一个数值,抬高一下,如加0.5.
27-28-合并与分割
numpy中使用concat,在pytorch中使用更加简写的cat
完成一个拼接
两个向量维度相同,想要拼接的维度上的值可以不同,但是其它维度上的值必须相同。
例子:将两班级的成绩合并起来
a[class 1-4, students, scores]
b[class 5-9, students, scores]
In[4]: a = torch.rand(4,32,8)
In[5]: b = torch.rand(5,32,8)
In[6]: torch.cat([a,b],dim=0).shape
# 将a,b在第0个维度进行合并
Out[6]: torch.Size([9, 32, 8])
# 结果就是9个班级的成绩
行拼接:[4, 4] 与 [5, 4] 以 dim=0(行)进行拼接 —> [9, 4] 9个班的成绩合起来
列拼接:[4, 5] 与 [4, 3] 以 dim=1(列)进行拼接 —> [4, 8] 每个班合成8项成绩
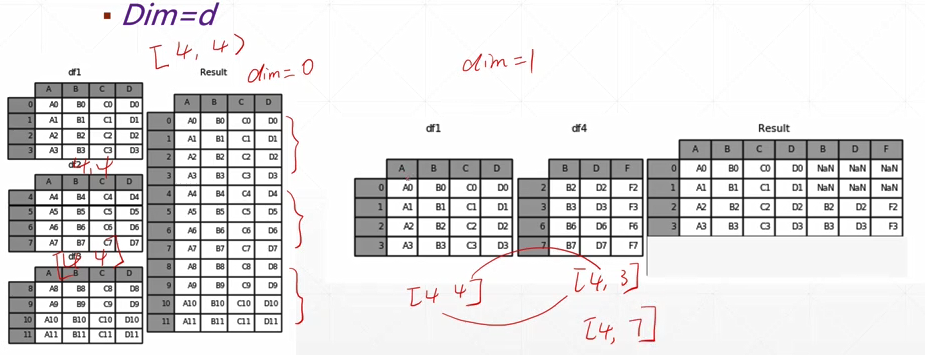
例2:
In[7]: a1 = torch.rand(4,3,32,32)
In[8]: a2 = torch.rand(5,3,32,32)
In[9]: torch.cat([a1,a2],dim=0).shape # 合并第1维 理解上相当于合并batch
Out[9]: torch.Size([9, 3, 32, 32])
In[11]: a2 = torch.rand(4,1,32,32)
In[12]: torch.cat([a1,a2],dim=1).shape # 合并第2维 理解上相当每张图片有rgbα四个通道
Out[12]: torch.Size([4, 4, 32, 32])
In[13]: a1 = torch.rand(4,3,16,32)
In[14]: a2 = torch.rand(4,3,16,32)
In[15]: torch.cat([a1,a2],dim=3).shape # 合并第3维 理解上相当于合并照片的上下两半
Out[15]: torch.Size([4, 3, 16, 64])
In[17]: a1 = torch.rand(4,3,32,32)
In[18]: torch.cat([a1,a2],dim=0).shape
RuntimeError: invalid argument 0: Sizes of tensors must match except in dimension 0.
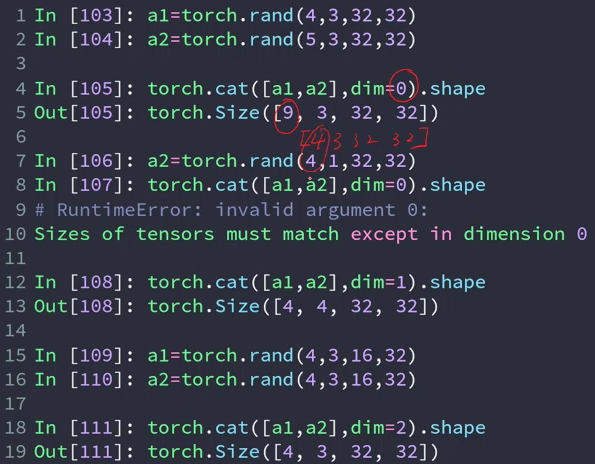
- stack
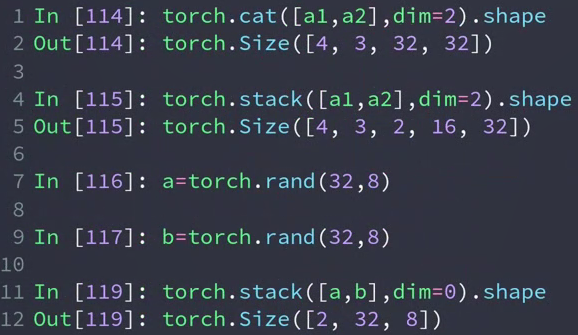
创造一个新的维度(代表了新的组别)
要求两个tensor的size完全相同
In[19]: a1 = torch.rand(4,3,16,32)
In[20]: a2 = torch.rand(4,3,16,32)
In[21]: torch.cat([a1,a2],dim=2).shape # 合并照片的上下部分
Out[21]: torch.Size([4, 3, 32, 32])
In[22]: torch.stack([a1,a2],dim=2).shape # 添加了一个维度 一个值代表上半部分,一个值代表下半部分。 这显然是没有cat合适的。
Out[22]: torch.Size([4, 3, 2, 16, 32])
In[23]: a = torch.rand(32,8)
In[24]: b = torch.rand(32,8)
In[25]: torch.stack([a,b],dim=0).shape # 将两个班级的学生成绩合并,添加一个新的维度,这个维度的每个值代表一个班级。显然是比cat合适的。
Out[25]: torch.Size([2, 32, 8])
In[26]: a.shape
Out[26]: torch.Size([32, 8])
In[27]: b = torch.rand([30,8])
In[28]: torch.stack([a,b],dim=0)
RuntimeError: invalid argument 0: Sizes of tensors must match except in dimension 0

- split
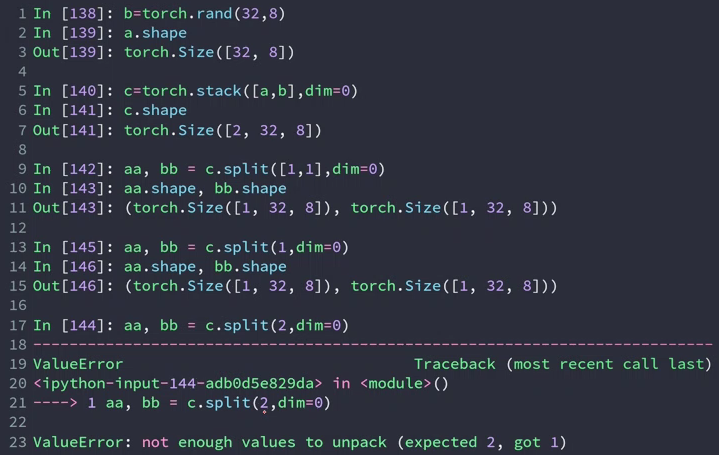
按长度进行拆分:单元长度/数量
长度相同给一个固定值,长度不同给一个列表
In[48]: a = torch.rand(32,8)
In[49]: b = torch.rand(32,8)
In[50]: c = torch.rand(32,8)
In[51]: d = torch.rand(32,8)
In[52]: e = torch.rand(32,8)
In[53]: f = torch.rand(32,8)
In[54]: s = torch.stack([a,b,c,d,e,f],dim=0)
In[55]: s.shape
Out[55]: torch.Size([6, 32, 8])
In[57]: aa,bb = s.split(3,dim=0) # 按数量切分,可以使用一个常数
In[58]: aa.shape, bb.shape
Out[58]: (torch.Size([3, 32, 8]), torch.Size([3, 32, 8]))
In[59]: cc,dd,ee = s.split([3,2,1],dim=0) # 按单位长度切分,可以使用一个列表
In[60]: cc.shape, dd.shape, ee.shape
Out[60]: (torch.Size([3, 32, 8]), torch.Size([2, 32, 8]), torch.Size([1, 32, 8]))
In[61]: ff,gg = s.split(6,dim=0) # 只能拆成一个,返回一个tensor,不能用两个tensor接收
ValueError: not enough values to unpack (expected 2, got 1)
- chunk
按数量进行拆分
chunk中的参数是要切成几份;split的常数是每份有几个
In[63]: s.shape
Out[63]: torch.Size([6, 32, 8])
In[64]: aa,bb = s.chunk(2,dim=0)
In[65]: aa.shape, bb.shape
Out[65]: (torch.Size([3, 32, 8]), torch.Size([3, 32, 8]))
In[66]: cc,dd = s.split(3,dim=0)
In[67]: cc.shape,dd.shape
Out[67]: (torch.Size([3, 32, 8]), torch.Size([3, 32, 8]))
29-30-数学运算
- 基础运算
可以使用 + - * / (推荐),也可以使用 torch.add, mul, sub, div

b:使用broadcast [4] → [3,4]
//二斜线表示整除
- matmul
matmul 表示 matrix mul,矩阵乘法
*表示的是element-wise,按元素一个一个操作, 是两个同样维度的向量/矩阵每一个元素分别相乘
torch.mm(a,b) 只能计算2D 不推荐
torch.matmul(a,b) 可以计算更高维度,落脚点依旧在行与列。 推荐
@是matmul的重载形式

实例:神经网络中线性层的相加
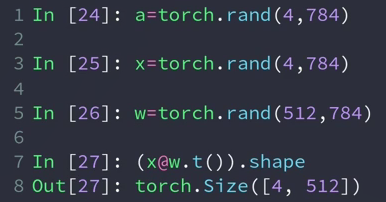
线性层的计算 : x @ w.t() + b
x是4张照片且已经打平了 (4, 784)
我们希望 (4, 784) —> (4, 512)
这样的话w因该是 (784, 512)
但由于pytorch默认 第一个维度是 channel-out(目标),第二个维度是 channel-in (输入),所以需要用一个转置
.t() 只适合2D,高维用transpose
- 2维以上的matmul
对于2维以上的matrix multiply , torch.mm(a,b)就不行了。
运算规则:只取最后的两维做矩阵乘法
对于 [b, c, h, w] 来说,b,c 是不变的,图片的大小在改变;并且也并行的计算出了b,c。也就是支持多个矩阵并行相乘。
对于不同的size(例33),如果符合broadcast,先执行broadcast,在进行矩阵相乘。

- power
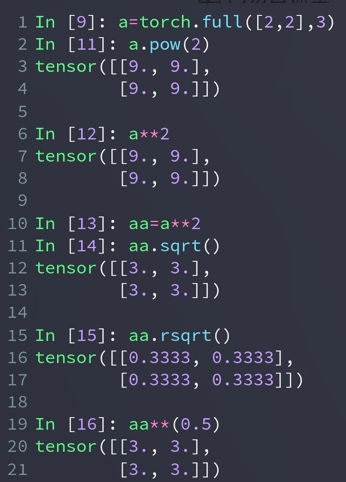
pow(a, n):a的n次方
** 也表示次方(可以是2,0.5,0.25,3),推荐
sqrt() 表示 square root 平方根
rsqrt() 表示平方根的倒数
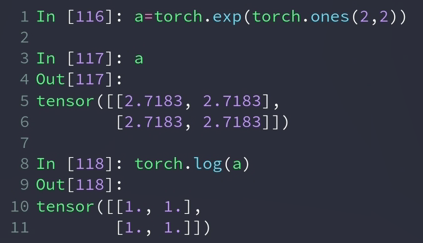
- exp log
exp(n) 表示:e的n次方
log(a) 表示:ln(a)
log2() 、 log10()
In[22]: torch.log2(a)
Out[22]:
tensor([[1.4427, 1.4427],
[1.4427, 1.4427]])
In[23]: torch.log10(a)
Out[23]:
tensor([[0.4343, 0.4343],
[0.4343, 0.4343]])
- approximation
不太常用
floor、ceil 向下取整、向上取整
round 4舍5入
trunc、frac 裁剪

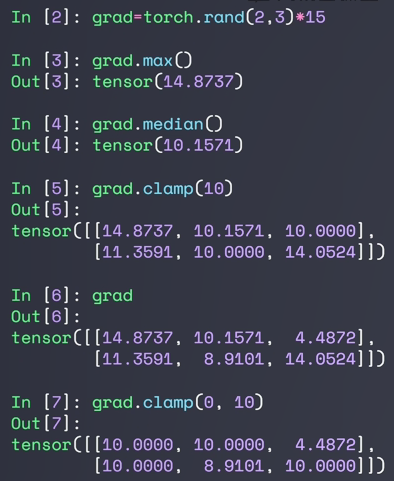
- clamp
gradient clipping 梯度裁剪
(min) 限定最小值,小于min的都变为min
(min, max) 大于这个区间的都变为max,小于的都变为min
梯度爆炸:一般来说,当梯度达到100左右的时候,就已经很大了,正常在10左右,通过打印梯度的模来查看 w.grad.norm(2)
对于w的限制叫做weight clipping,对于weight gradient clipping称为 gradient clipping。
31-32-属性统计
- norm
norm指的是范数,并不是normalize。normalize是归一化,例如 batch_norm。
向量的范数,就是表示这个原有集合的大小。
矩阵的范数,就是表示这个变化过程的大小的一个度量。
总结起来一句话,范数(norm),是具有“长度”概念的函数。
norm(1, 一范数,所有元素的绝对值之和
norm(2, 二范数,所有元素的平方和并开根号
不加dim参数,默认所有维度
从shape出发,加入dim后,这个dim就会消失(做Norm)
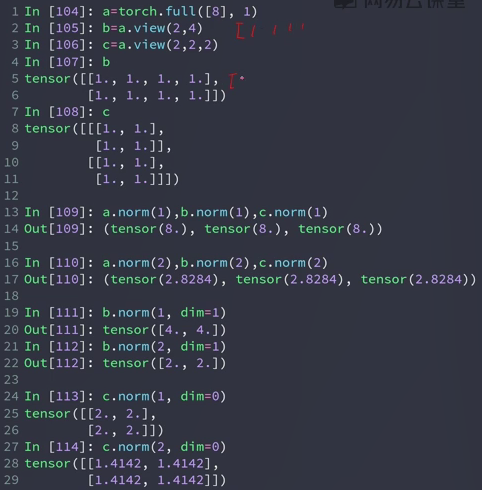
In[3]: a = torch.full([8],1)
In[4]: b = a.view(2,4)
In[5]: c = a.view(2,2,2)
In[6]: b
Out[6]:
tensor([[1., 1., 1., 1.],
[1., 1., 1., 1.]])
In[7]: c
Out[7]:
tensor([[[1., 1.],
[1., 1.]],
[[1., 1.],
[1., 1.]]])
In[8]: a.norm(1), b.norm(1), c.norm(1)
Out[8]: (tensor(8.), tensor(8.), tensor(8.)) # 一范数是所有元素绝对值的求和,八个1所以一范数是8
In[9]: a.norm(2), b.norm(2), c.norm(2)
Out[9]: (tensor(2.8284), tensor(2.8284), tensor(2.8284))
In[10]: b.norm(1,dim=1) # 一范数,[1., 1., 1., 1.]→4.,[1., 1., 1., 1.]→4.
Out[10]: tensor([4., 4.]) # 就shape来讲 [2,4] norm之后 --> [2]
In[16]: b.norm(1,dim=0)
Out[16]: tensor([2., 2., 2., 2.]) # shape [2,4] ---> [4]
In[11]: b.norm(2,dim=1)
Out[11]: tensor([2., 2.])
In[12]: c.norm(1,dim=0) # [2,2,2],在0维度做求1范数,那么这个维度就将消掉,得到shape为[2,2]
Out[12]:
tensor([[2., 2.],
[2., 2.]])
In[14]: c.norm(2,dim=0)
Out[14]:
tensor([[1.4142, 1.4142],
[1.4142, 1.4142]])
- mean,sum,min,max,prod
max() 求最大的值
min() 求最小的值
mean() 求平均值 mean = sum / size
prod() 累乘
sum() 求和
argmax() 返回最大值元素的索引
argmin() 返回最大值元素的索引
argmax(dim=l) 求l维中,最大元素的位置,这样的话这一维将消失。
以上这些,如果不加参数,会先打平,在计算,所以对于 argmax 和 argmin来说得到的是打平后的索引。
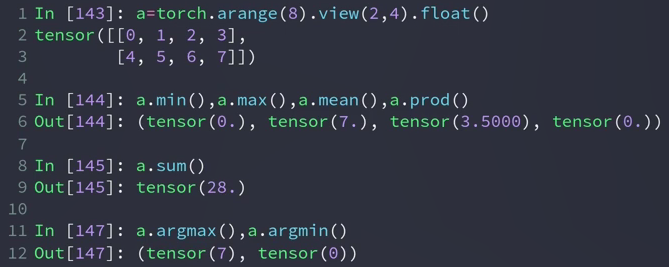
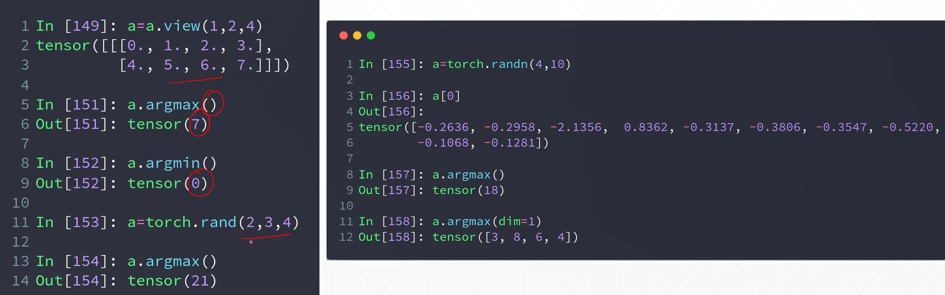
例158,dim=1,获取4张照片预测值最大的位置,这个位置决定了它是数字几
- keepdim
使用max(dim=) 函数配上dim参数,可以很好的返回最大值与该值的位置
argmax 其实是 max 的一部分(位置)
keepdim=True 设置这个参数后,维度得以保留,与原来的维度是一样的。

-
top-k / k-th
- topk
由于max只能找出一个最大,如果想找最大的几个就做不到了。
topk(k, 比max提供更多的信息,适用于特定的场合。
topk(k, 指的是返回概率最大的的 k 组数据以及位置
largest=False 求概率最小的 k 组
例如:对于一张照片,他的概率是[0.2, 0.3, 0.1, 0.2, 0.1, 0.1],使用topk(3) 会得到概率最大的三个数[0.3, 0.2, 0.2] 以及位置[1, 0, 3]
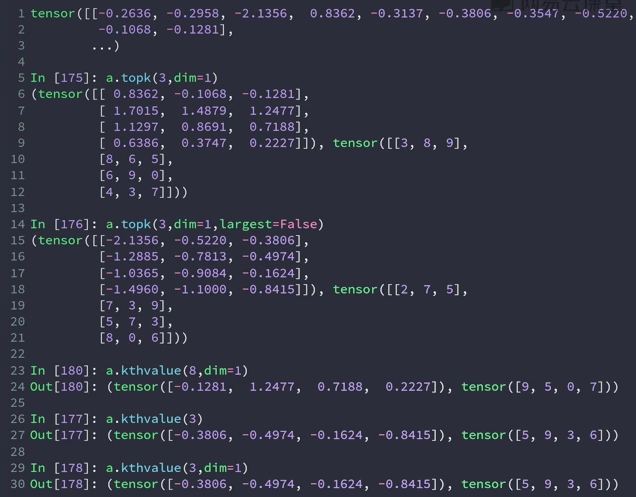
In[33]: a
Out[33]:
tensor([[ 0.0234, 0.6830, -0.1518, 0.4595, -1.5634, 0.5534, 0.9934, -1.1536,
0.3124, -1.4103],
[ 0.6339, 1.5724, 0.2552, 1.0917, -1.4003, 0.5165, 0.8891, -2.0315,
0.4666, 1.4355],
[ 1.6149, 0.2364, 0.3789, -0.3974, -0.1433, 0.9235, 0.6730, 0.3575,
2.0742, 0.8954],
[-0.1019, 1.6405, -1.3493, 0.5554, -0.0533, 0.0450, 0.2018, -0.1688,
-1.2579, -0.7906]])
In[34]:
In[34]: a.topk(3,dim=1)
Out[34]:
torch.return_types.topk(
values=tensor([[0.9934, 0.6830, 0.5534], # 返回概率最大的前3个
[1.5724, 1.4355, 1.0917],
[2.0742, 1.6149, 0.9235],
[1.6405, 0.5554, 0.2018]]),
# shape的话 从[4, 10] ---> [4,3]
indices=tensor([[6, 1, 5], # 最可能是6,1次之,5次之
[1, 9, 3],
[8, 0, 5],
[1, 3, 6]]))
In[35]: a.topk(3,dim=1,largest=False)
Out[35]:
torch.return_types.topk(
values=tensor([[-1.5634, -1.4103, -1.1536],
[-2.0315, -1.4003, 0.2552],
[-0.3974, -0.1433, 0.2364],
[-1.3493, -1.2579, -0.7906]]),
indices=tensor([[4, 9, 7], # 最不可能是4,9次之,7次之
[7, 4, 2],
- kthvalue
kthvalue(i, dim=j) 求 j 维上,第 i 小的元素以及位置。dim默认为1。
keepdim=True 会保持维度
In[36]: a.kthvalue(8,dim=1) # 求1维,第8小
Out[36]:
torch.return_types.kthvalue(
values=tensor([0.5534, 1.0917, 0.9235, 0.2018]),
indices=tensor([5, 3, 5, 6]))
In[37]: a.kthvalue(3)
Out[37]:
torch.return_types.kthvalue(
values=tensor([-1.1536, 0.2552, 0.2364, -0.7906]),
indices=tensor([7, 2, 1, 9]))
In[38]: a.kthvalue(3,dim=1)
Out[38]:
torch.return_types.kthvalue(
values=tensor([-1.1536, 0.2552, 0.2364, -0.7906]),
indices=tensor([7, 2, 1, 9]))

- compare
, >=, <, <=, !=, ==
进行比较后,返回的是一个 bytetensor,不再是floattensor,由于pytorch中所有的类型都是数值,没有True or False ,为了表达使用整型的1或0
torch.eq(a,b) 判断每一个元素是否相等,返回 bytetensor
torch.equal(a,b) 返回True或False
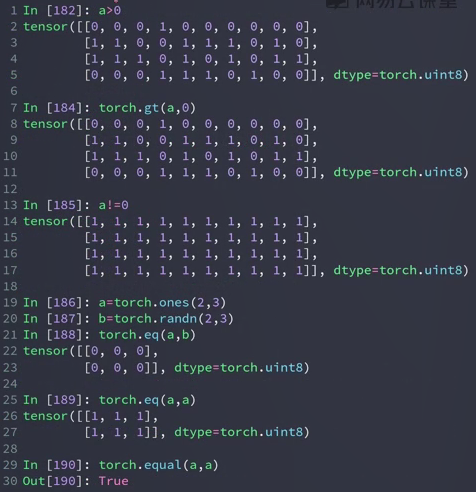
numpy与pytorch比较操作的方法,还是推荐 符号 > < ..
| Numpy | PyTorch |
|---|---|
| np.less | x.lt |
| np.less_equal | x.le |
| np.less_equal | x.le |
| np.less_equal | x.le |
| np.equal | x.eq |
| np.not_equal | x.ne |
33-高阶操作
- where
torch.where(condition, x, y) → Tensor
针对于x而言,如果其中的每个元素都满足condition,就返回x的值;如果不满足condition,就将y对应位置的元素或者y的值替换x的值,最后返回结果。
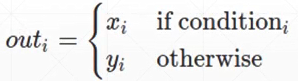

- gather
torch.gather(input, dim, index, out=None) → Tensor
沿给定轴 dim ,将输入索引张量 index 指定位置的值进行聚合.
input (Tensor) – 源张量
dim (int) – 索引的轴
index (LongTensor) – 聚合元素的下标(index需要是torch.longTensor类型)
out (Tensor, optional) – 目标张量
对一个 3 维张量,输出可以定义为:
out[i][j][k] = input[index[i][j][k]][j][k] # if dim == 0
out[i][j][k] = input[i][index[i][j][k]][k] # if dim == 1
out[i][j][k] = input[i][j][index[i][j][k]] # if dim == 2
a = torch.Tensor([[1,2],
[3,4]])
b = torch.gather(a,1,torch.LongTensor([[0,0],[1,0]]))
#1. 取各个元素行号:[(0,y)(0,y)][(1,y)(1,y)]
#2. 取各个元素值做y:[(0,0)(0,0)][(1,1)(1,0)]
#3. 根据得到的索引在输入中取值
#[1,1],[4,3]
c = torch.gather(a,0,torch.LongTensor([[0,0],[1,0]]))
#1. 取各个元素列号:[(x,0)(x,1)][(x,0)(x,1)]
#2. 取各个元素值做x:[(0,0)(0,1)][(1,0)(0,1)]
#3. 根据得到的索引在输入中取值
#[1,2],[3,2]
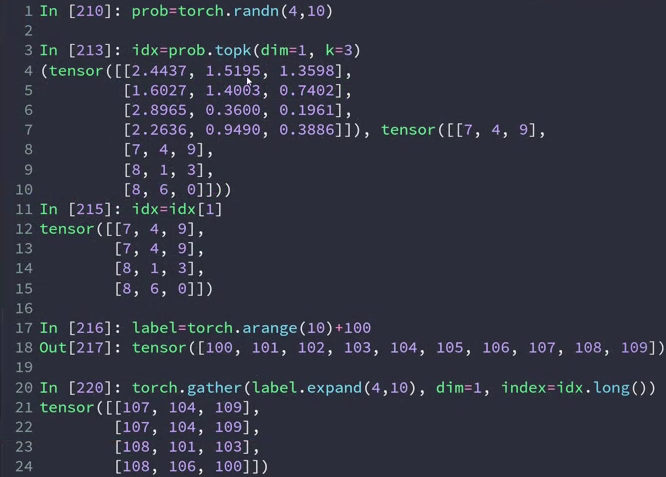
(0,7)(0,4)(0,9)
(1,7)(1,4)(1,9)
(2,8)(2,1)(2,3)
(3,8)(3,6)(3,9)
34-35-什么是梯度
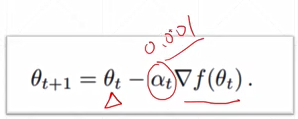
寻找全局极小值时的影响因素:
初始化
learning rate(小一点)
动量(惯性,冲出局部极小)
36-常见函数的梯度
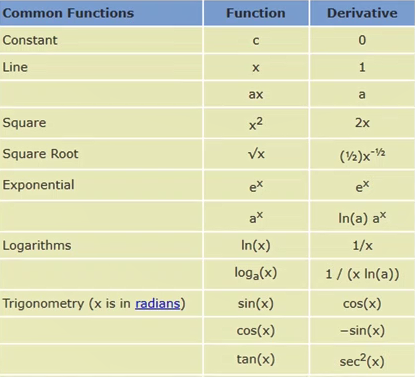
导数:给定一个方向;梯度:所有方向的综合。对于一维函数只有一个方向,所以两者基本是一个东西。
y=xw+b x作为神经网络的输入。wb为神经网络的参数,是要优化的目标

y=x w2+b2
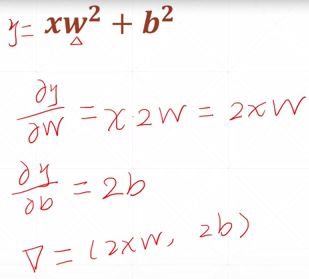
y=x ew+eb
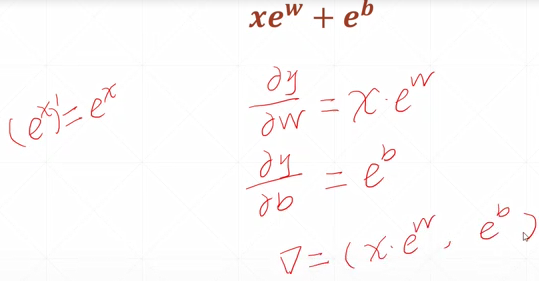
[y-(xw+b)]^2 可理解为线性感知器的输出与真实的label(y)间的均方差
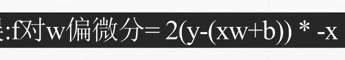
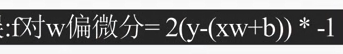
y log(x w+b)
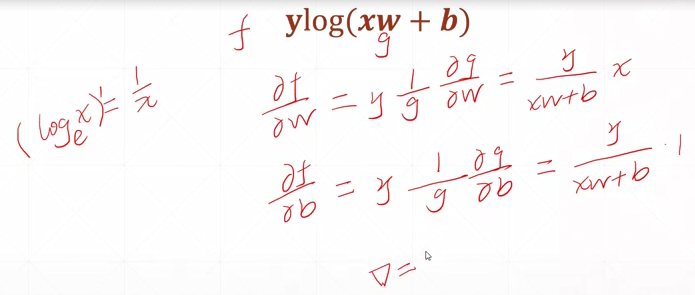
37-40-激活函数与Loss的梯度
激活函数:
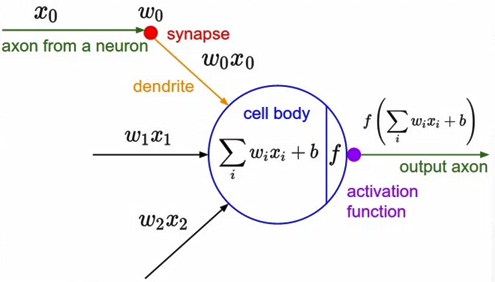
输入小于某个值时没有输出,大于某个值时给出一个固定的响应(青蛙实验)

- Sigmoid函数
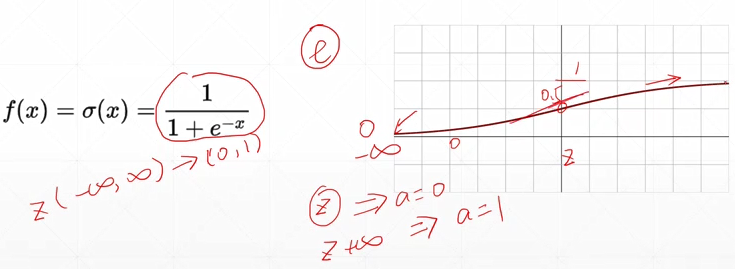
常被用作神经网络的激活函数,将变量映射到0-1之间。
求导:
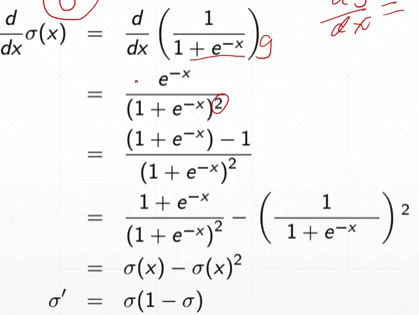
torch.sigmoid


- Tanh
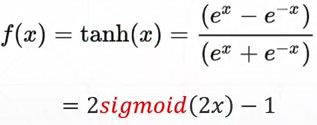

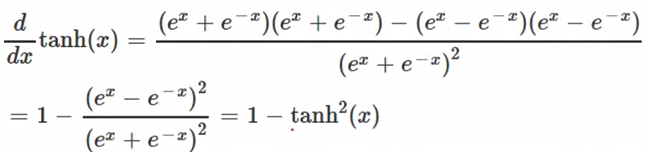

- Rectified Linear Unit 整形的线性单元 ReLU
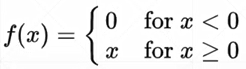

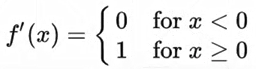
极大减少了梯度离散与梯度爆炸的情况
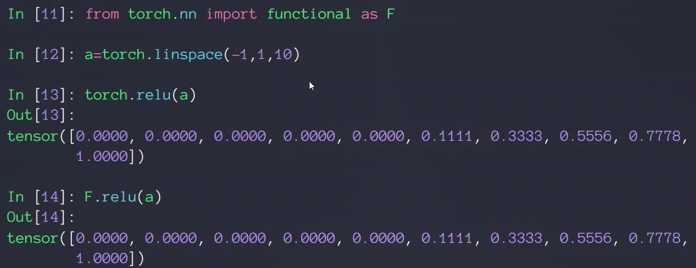
- typical loss

mean squared Error 均方误差MSE
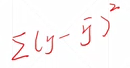
y减去y的预测值的平方和
cross entropy loss 可用于二分类也可用于多分类,通常与softmax激活函数搭配使用
- MSE
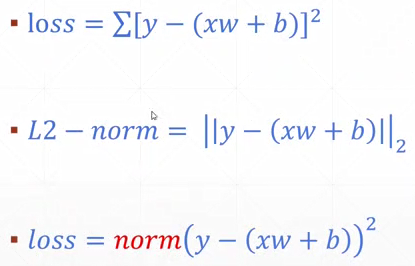
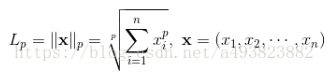
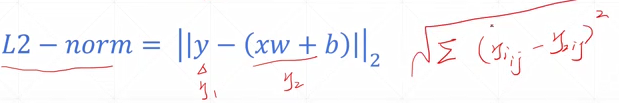
torch.norm(y-pred,2).pow(2)
梯度求解:
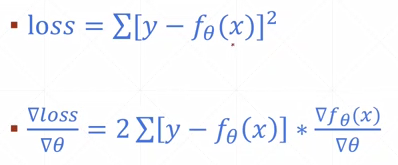
使用pytorch自动求导:

mse_loss(input,label)
input:预测值;label:目标值。维度为 [N1,N2,...,Nk,D] 的多维Tensor,其中最后一维D是类别数目。数据类型为float32或float64。
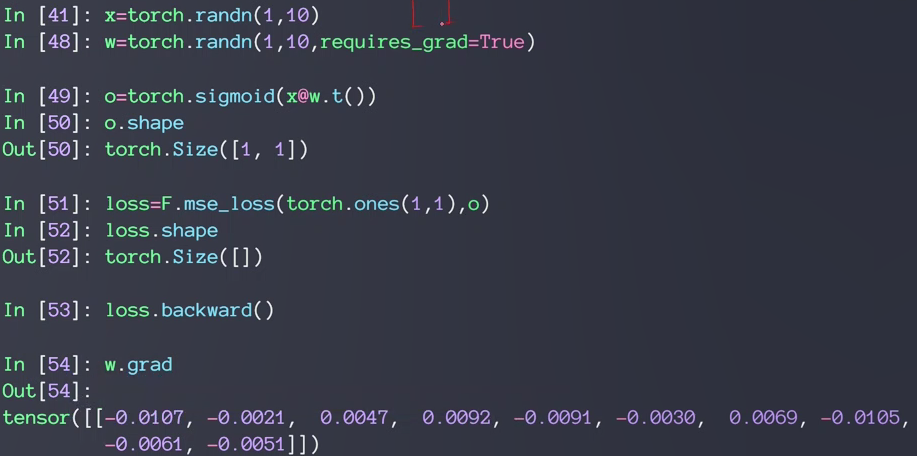
例21出错因为w没有标注需要求导信息
requests_grad:是否求导.默认为False,可以新建W时就加上requests_grad=true,或者后面使用requests_grad_()。
23还出错因为pytorch是动态图,做一步计算一步,图还没有更新。所以要用24把图重新计算,更新一遍
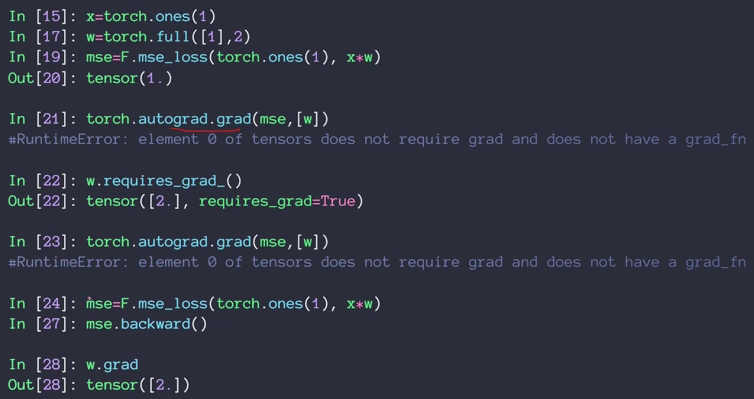
.backward() 从后往前传播
- gradient API

- softmax
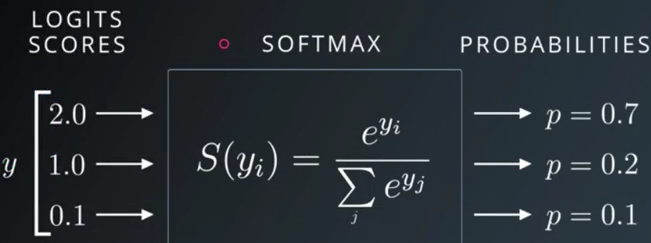
变成取值0-1,概率和为1.大的会较大,小的会压缩(大小差距变大)
求导:
i=j

i≠j

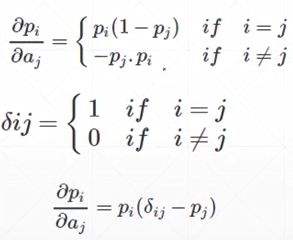
所以ij相等时候是正的,不等为负
F.softmax

例39 p[1],δP1/δai 所以i=1时的0.2274是正的; 例40 p[2]所以0.2425是正的 其他梯度是负的
41-42-感知器的梯度推导
- 单层感知器
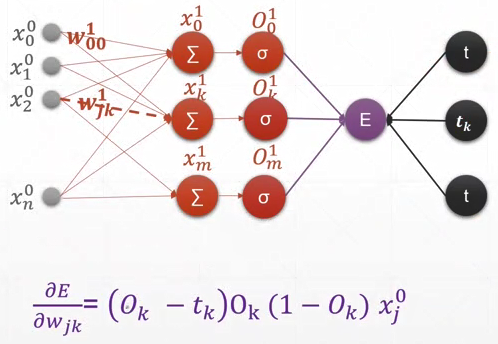
最终的loss对某层结点的求导公式:

输出只有一个,所以只有O0,没有O1O2……
跟神经元输出结点O及与其对应的j号结点的输入xj有关
- 多输出感知器

43-链式法则
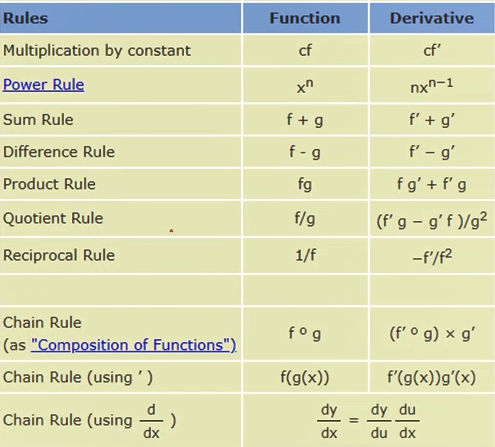


针对神经网络的具体实例:
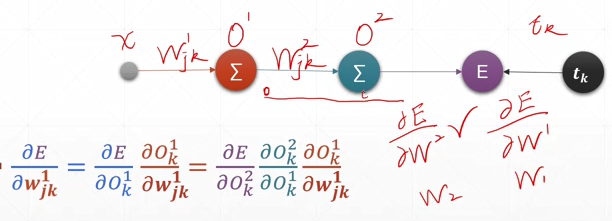
输入,经过一个隐藏层(橙色),再经过一个输出层(绿色),最后计算一个最终的loss。字母上标表示层数,下标表示编号
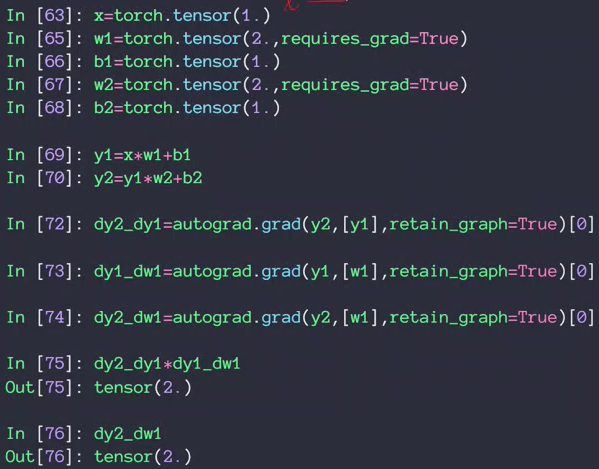

44-45-反向传播算法
- 多层感知器
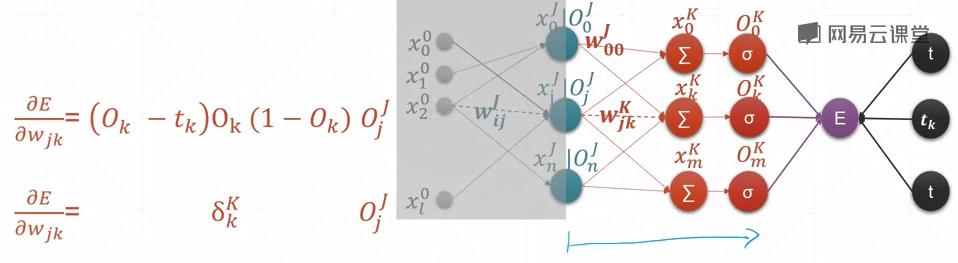


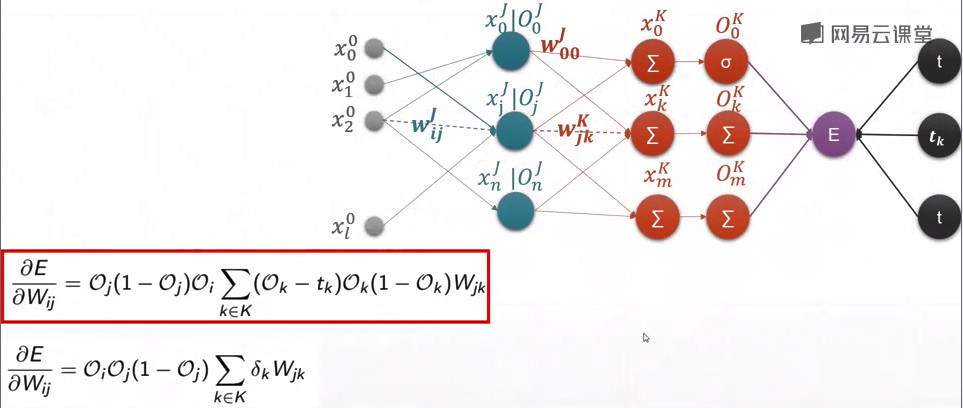
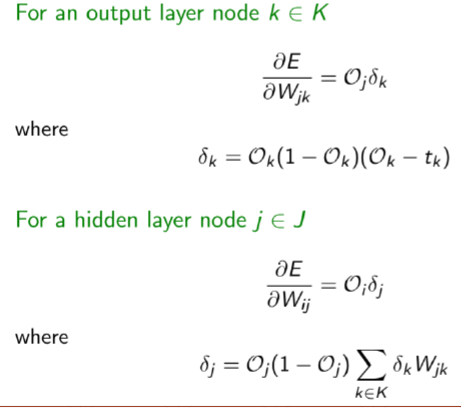
46-优化问题实战
2D函数优化实例:
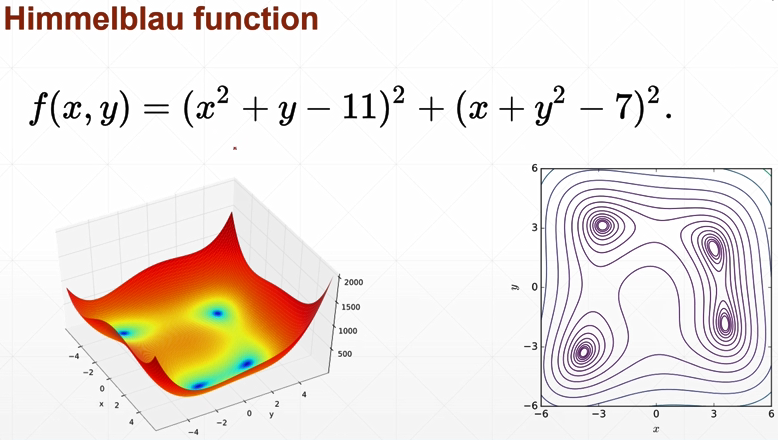
四个解都是全局最小解(因为一样大小)

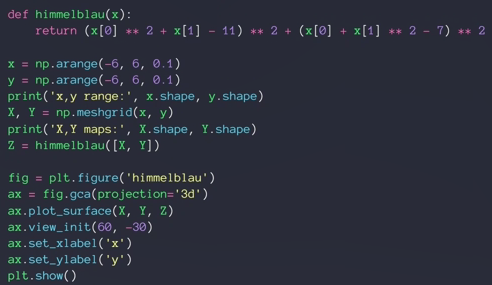
numpy.meshgrid()——生成网格点坐标矩阵
使用随机梯度下降方法求解:
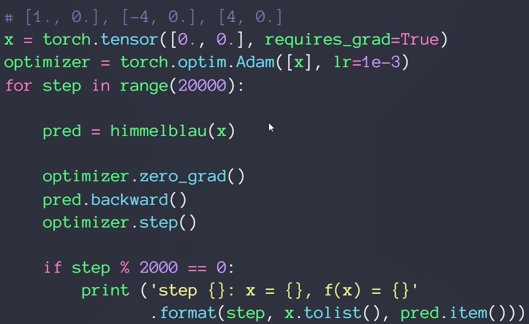

找到的是(3,2)这个局部极小值
初始化值改为4:

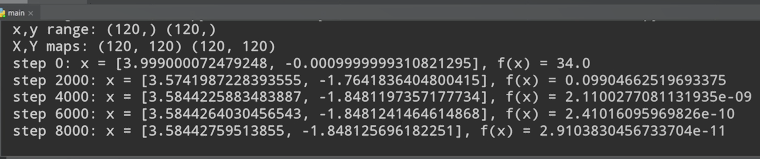

找到了另外的局部极小值
47-Logistic Regression逻辑回归





二分类问题:

大于0.5判断为1,小于0.5判断为0
多分类问题:

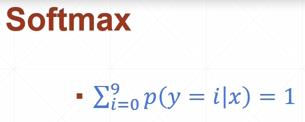
大的变的更大,小的聚集:

2,1→0.7,0.2 原来大两倍,现在大3.5倍

48-49-交叉熵
- entropy

不确定性 惊喜度
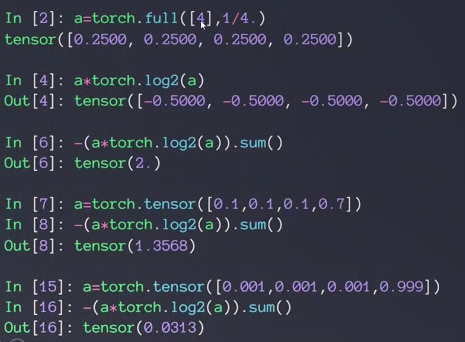
- cross entropy

OKL:KL Divergence散度,衡量两个分布的距离的关系

两个分布越相似DKL越接近于0
P=Q时,DKL=0,H(p,q)=H(p)

对于01encoding,H(p)=0
二分类:
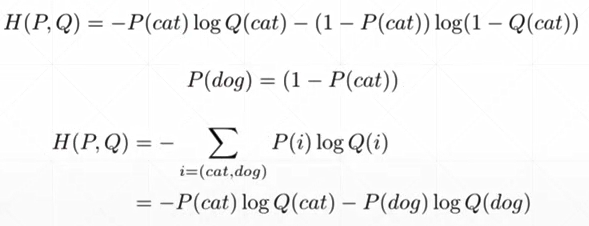
具体实例:

P为真实的分布,第一张图是狗。Q是Pθ,是模型的分布
理想情况:

对于分类问题为什么不使用MSE

用sigmoid搭配MSE很容易出现sigmoid饱和的现象,会出现梯度离散;
cross entropy梯度概率信息更大,收敛得更快
但由于MSE梯度求导更简单,所以有时候可以一试
小结:
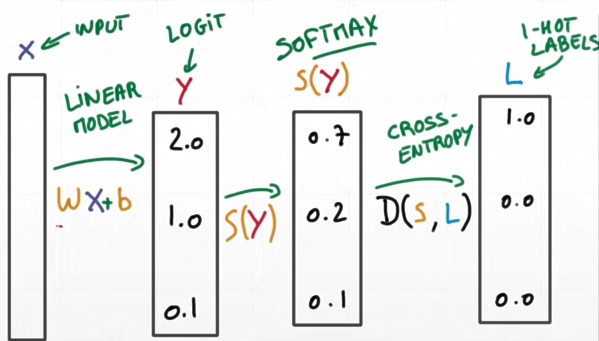
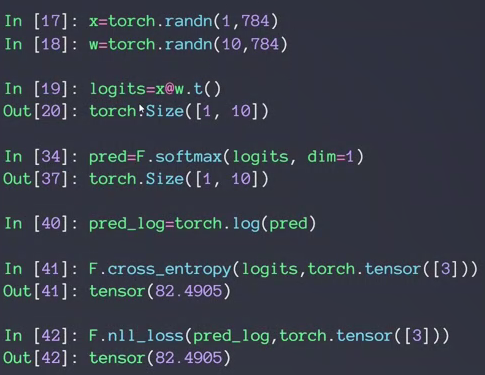
50-多分类问题实战
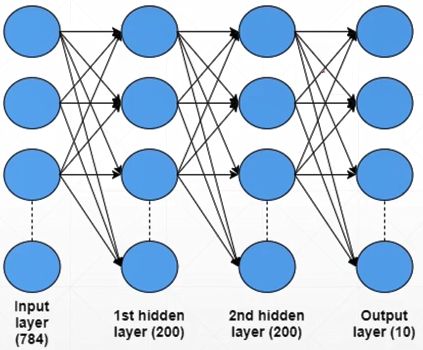
十层 代表十分类
网络tensor定义和forward过程:
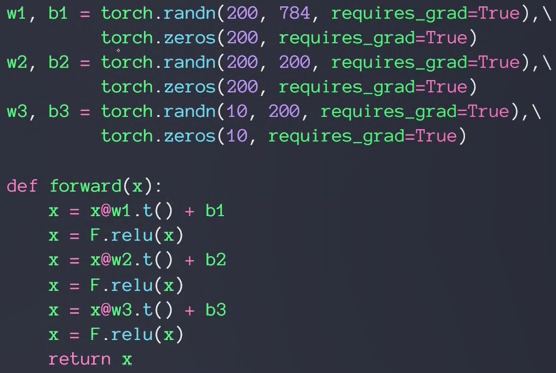
新建三个线性层
第一层,输入784,可以想象成28×28,也就是784降维成200的过程。w1b1都需要梯度信息
第二层,隐藏层,没有降维过程,不代表没有作用/功能,比如特征提取
第三层,因为十分类所以最后输出结点应为10个
经过relu后得到logits,没有经过sigmoid或softmax的称为logits
最后的F.relu也可以不用
train:

定义一个优化器

发现loss长时间得不到更新,出现梯度离散,说明梯度信息接近于0
加上hekaiming初始化的代码
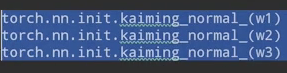
只对w初始化,因为b已经初始化为0了
发现改善
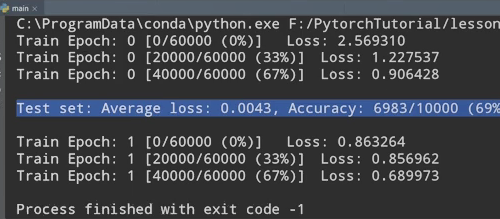
全连接层
- nn.Linear
nn.Linear(in_features,out_features)是用于设置网络中的全连接层的,全连接层的输入与输出都是二维张量,一般形状为[batch_size, size],不同于卷积层要求输入输出是四维张量。

加上relu以后:
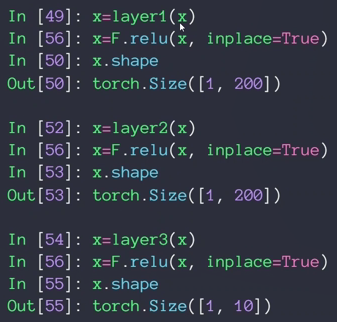
inplace=True的意思是进行原地操作,例如x=x+5,对x就是一个原地操作,不创建新的对象,直接对原始对象进行修改
step1:

step2:
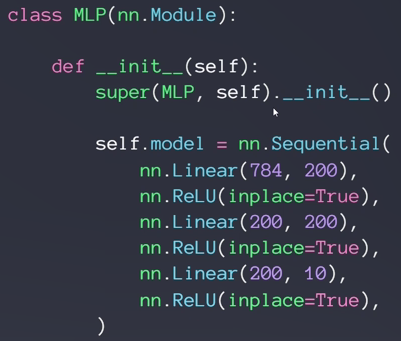
step3:

nn.Relu vs F.relu

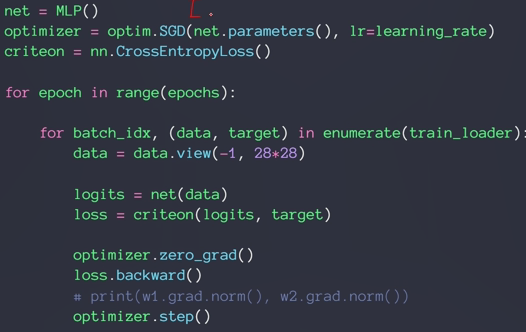
net.parameters()
激活函数与GPU加速
- SELU

- softplus
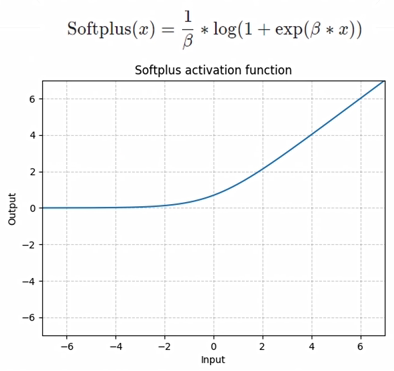
- GPU加速

可以使用torch.device()选取并返回抽象出的设备(这里选择了GPU),然后在定义的网络模块或者Tensor后面加上.to(device变量)就可以将它们搬到设备上了。
如有八张显卡,则cuda后可以是0-7的编号
.cuda()方法已经不推荐了
win7任务管理器里好像看不到GPU状态,一个比较笨的看NVIDIA GPU状态的方法就是在cmd里一直执行:
"C:\Program Files\NVIDIA Corporation\NVSMI\nvidia-smi.exe"
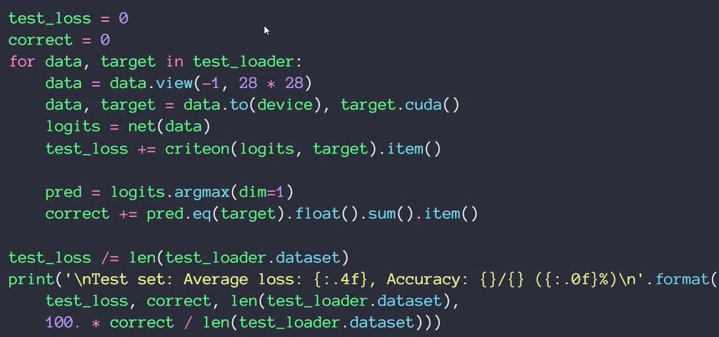
MNIST测试实战
- argmax

Visdom可视化
- tensorbroadX

- visdom
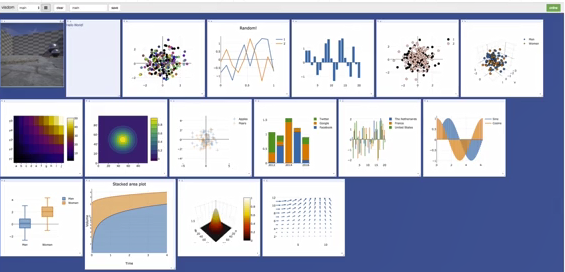
step1:install
pip install visdom
pip uninstall visdom是卸载

直接用pip安装的话在windows上面可能出现问题,先从Github上下载Visdom的源码,进入解压后的目录,执行:
pip install -e . 有个点号!
即从当前目录下的setup.py安装了Visdom。
step2:run server damon
python -m visdom.server
除了可能看到一些warning信息之外,正常运行时是这样的:
It's Alive!
INFO:root:Application Started
You can navigate to http://localhost:8097
访问http://localhost:8097

- 绘制单曲线:
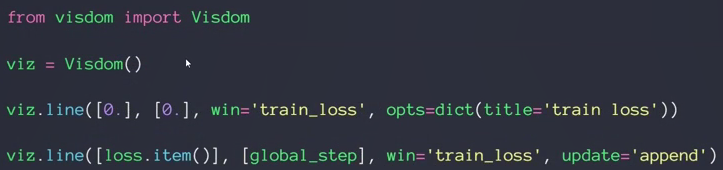
第三行创建一条曲线,首先创建y和x,这里初始只有一个点,所以yx都是0
win='train loss'是标志符

- 绘制多曲线
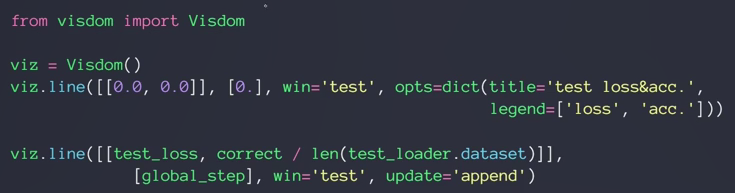
- 可视化 visdom x

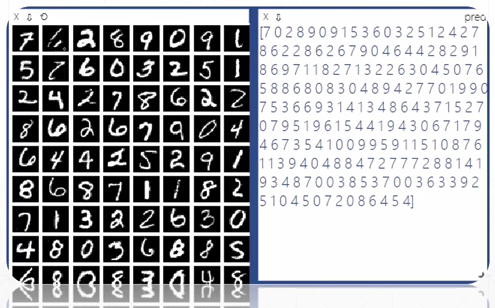
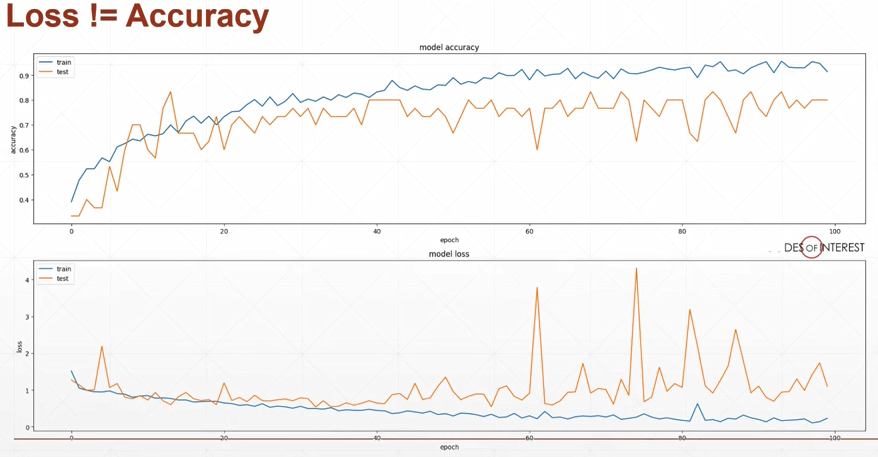
过拟合与欠拟合
实例1:房价随面积的变化
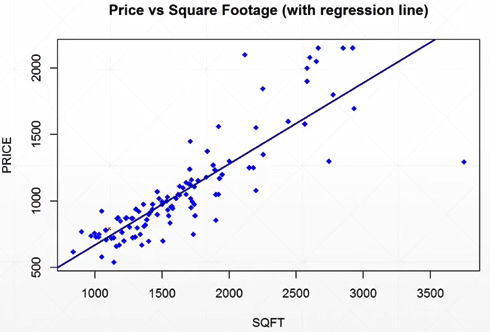
例2:GPA
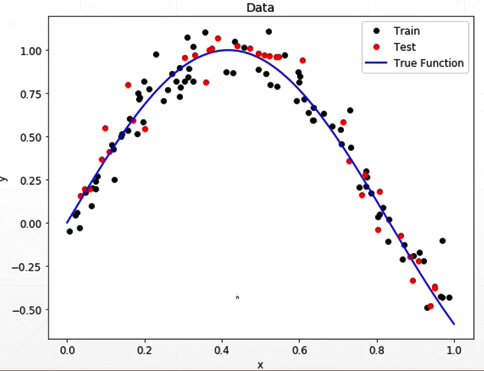
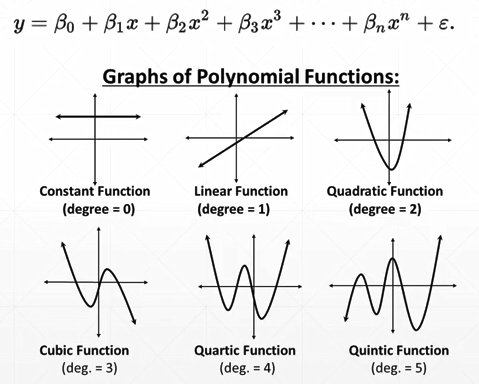
次方增加,网络表达能力变强
容量:
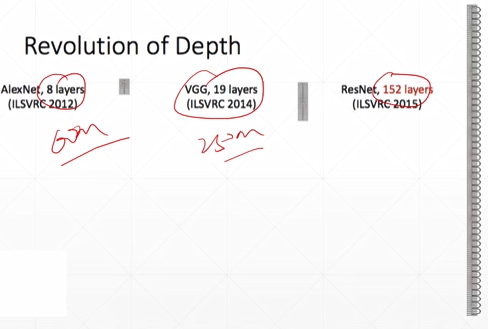
层数越大,学习能力越强
模型表达能力/复杂度<真实数据的复杂度:underfitting欠拟合
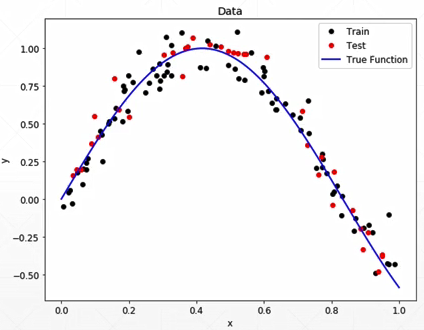
例子:WGAN

模型表达能力/复杂度>真实数据的复杂度:overfitting过拟合

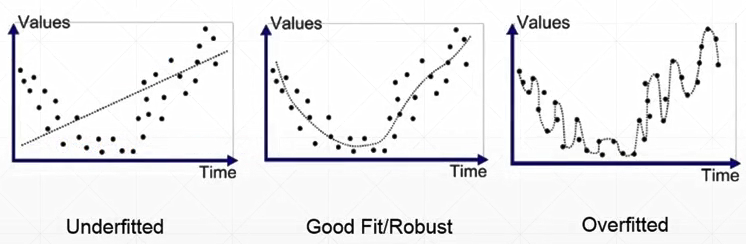
交叉验证
数据集拆分:


test while train
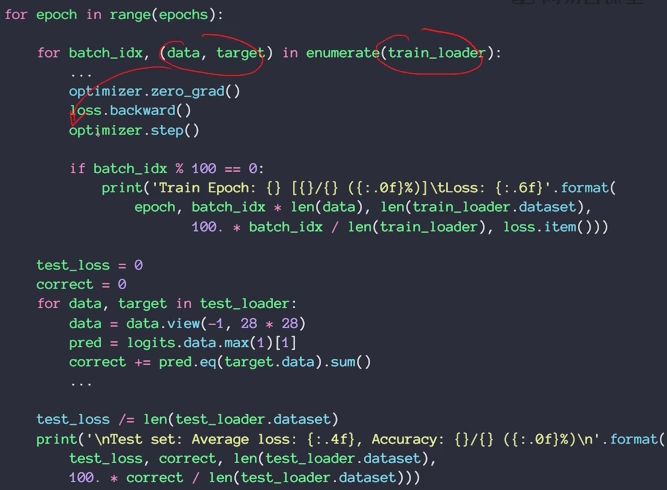
检测 如果已经overfitting了就取最好的状态
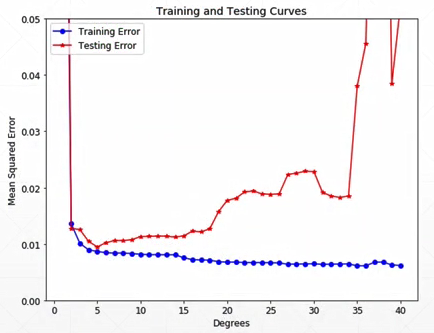
train-val-test

作弊:用train的数据做test,会导致代码的泛化能力变差
划分train和test数据的方式:

- 留出法(hold-out)
也就是直接划分,如将60k的训练集划分出10k来做验证集。
- K-fold cross validation
也就是K折交叉验证。这可以将验证集充分利用起来,比如在每个epoch重新划分这60k的数据,拿出其中的50k作为训练数据,其中的10k作为验证集。好处是这60k数据中每个都有可能是用来做train的,同时每个数据都有可能是做validation的,也同样防止了用train的来做validation出现的记样本的问题。
K-fold cross-validation划分成K份,每次取K-1份用来作为训练数据,1份用来做验证。
Regularization
如何防止/减轻overfitting

1.提供更多的数据(最简单 消耗最大)
2.降低模型复杂度(减少层数、)
3.正则化
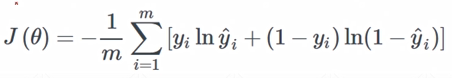
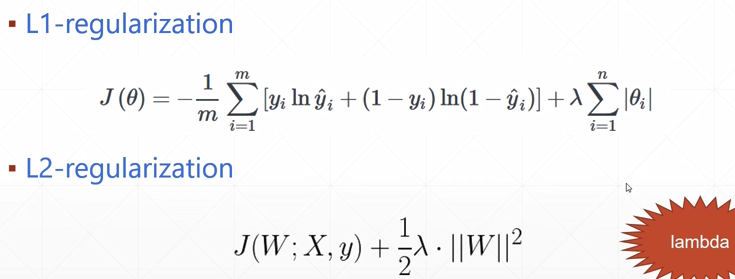
- L2 Regularization

- L1 Regularization
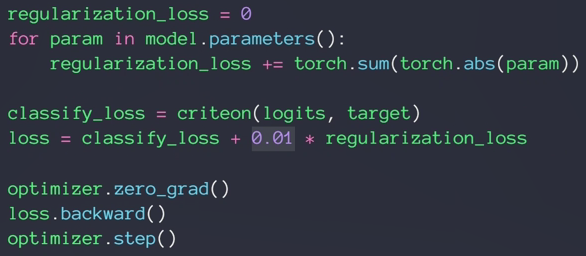
动量与学习率衰减
- 动量momentum
梯度更新的公式:
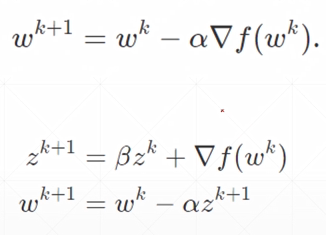
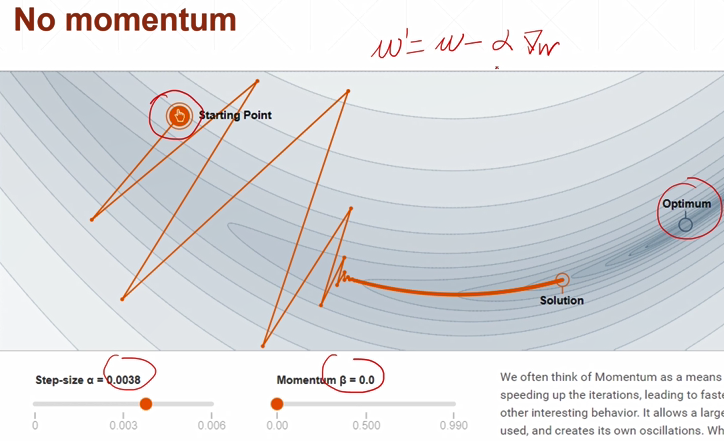
动量为0,没有找到全局最优解,并且出现很尖锐的更新方向
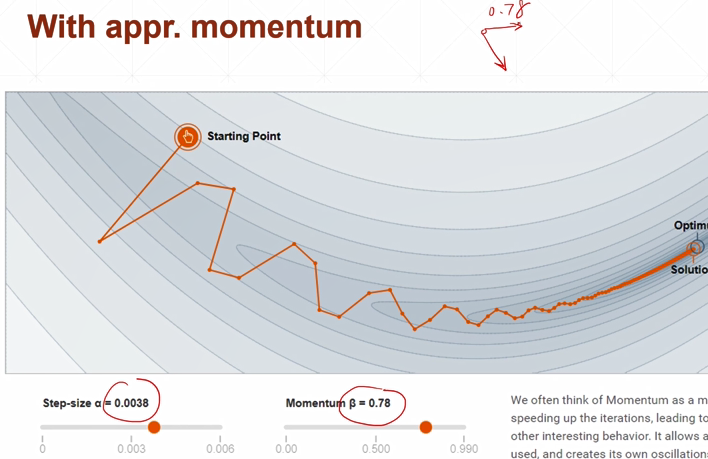
动量0.78,考虑历史方向会更多一点

- 学习率
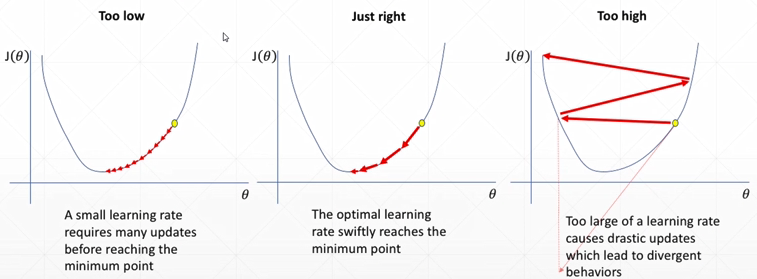
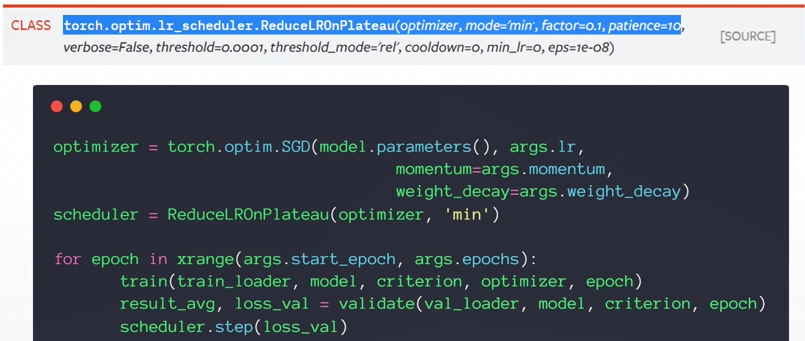
Early stopping, dropout等
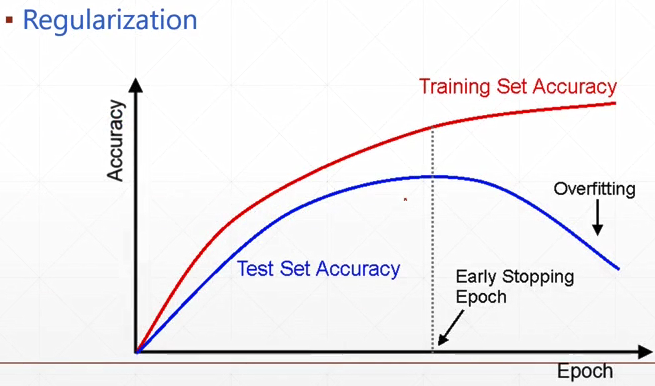
如何early stop

- DROPOUT
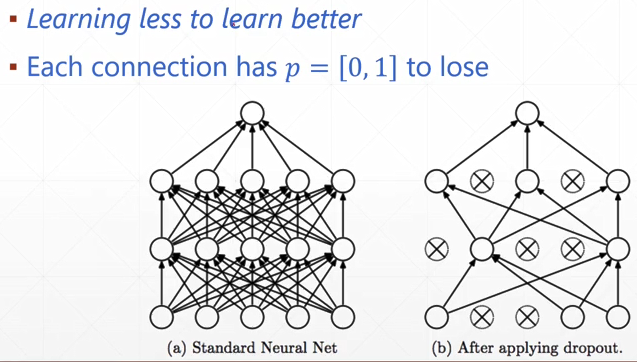
每段关系有一定概率断掉
加了dropout以后:
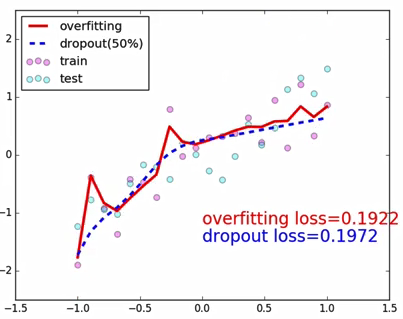
曲线更平滑
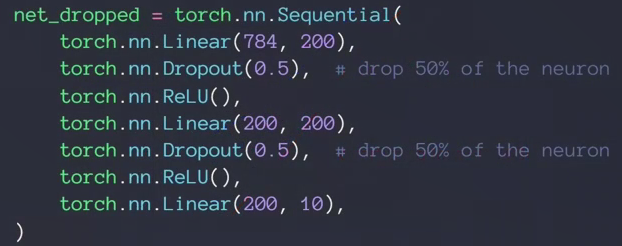

p=1时候说明所有线都有可能断掉,TensorFlow里相反
behavior between train and test:

- stochastic gradient descent随机梯度下降

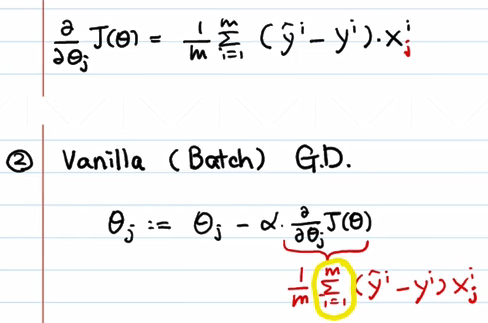
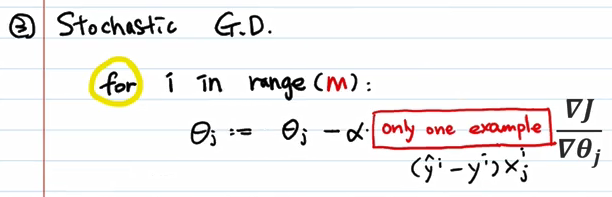
最大的原因是硬件问题,大容量的价格高,不可能把所有数据都加载进来计算
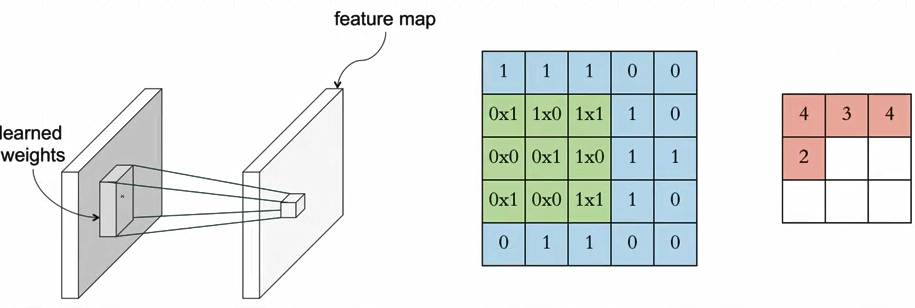
什么是卷积
图片的表示(MNIST为例,黑白图)


每个数据表示了这个点的灰度值,0-255.使用时可以除以255变成0-1,这就变成了一个浮点型的数组
对于彩色图,如果忽略阿尔法通道的话就是RGB,使用三张表。每个数值也是0-255(0-1)

全连接网络/pytorch里也叫线性层:

全值共享weight sharing

为什么成为卷积?
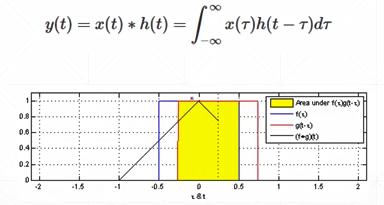
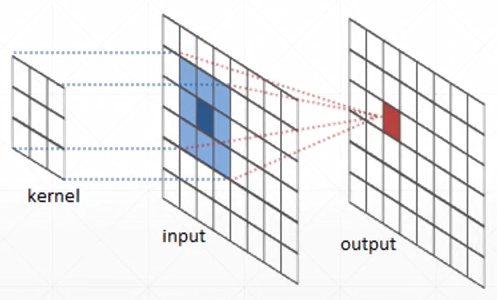
卷积神经网络
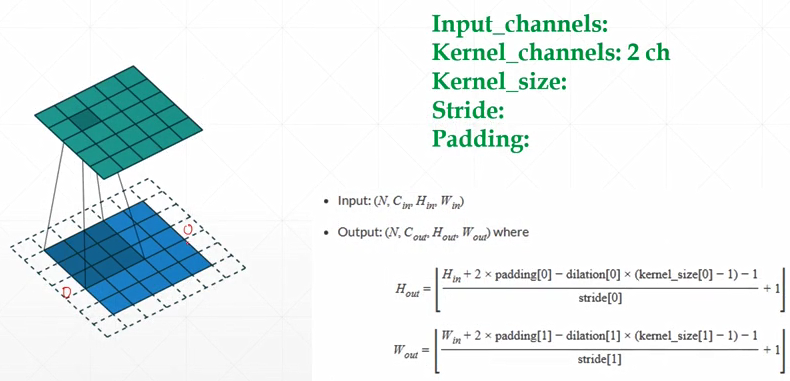

- nn.Conv2d

- inner weight & bias
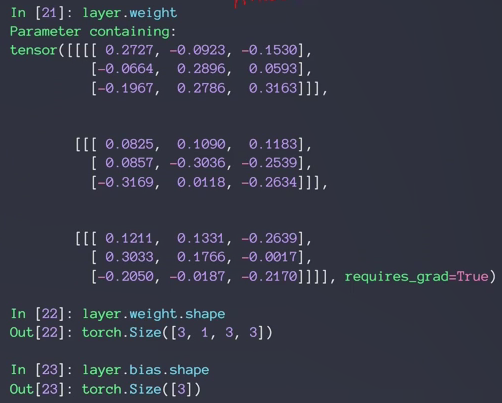
- F.conv2d
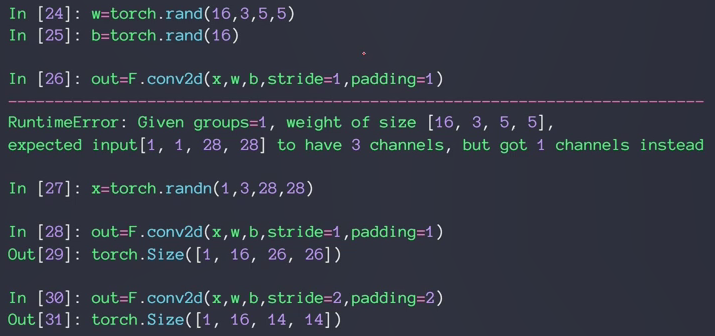
池化层与采样
下采样:
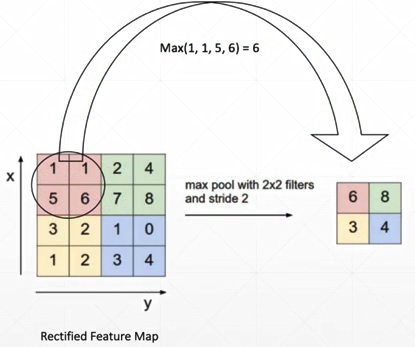
max pooling:
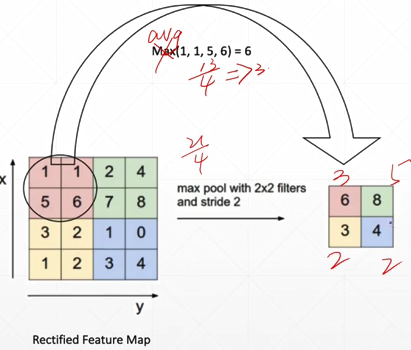
avg pooling:
reduce size:

上采样:
- F.interpolate

- RELU


Batch Norm
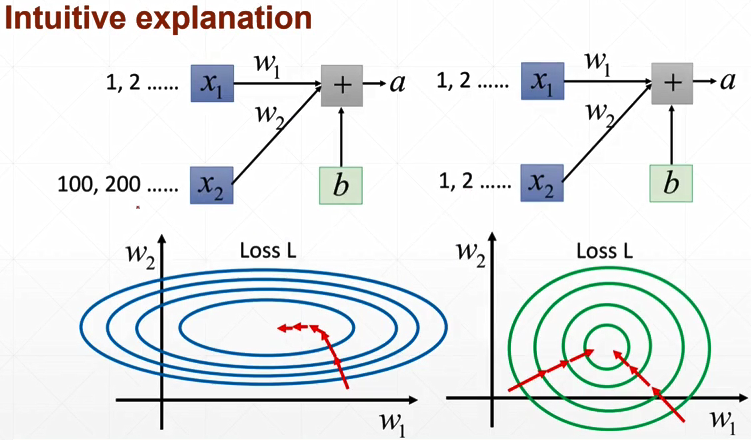
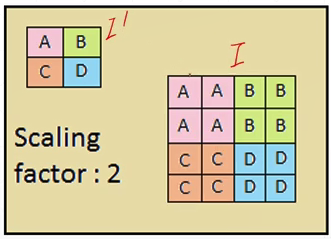
- feature scaling

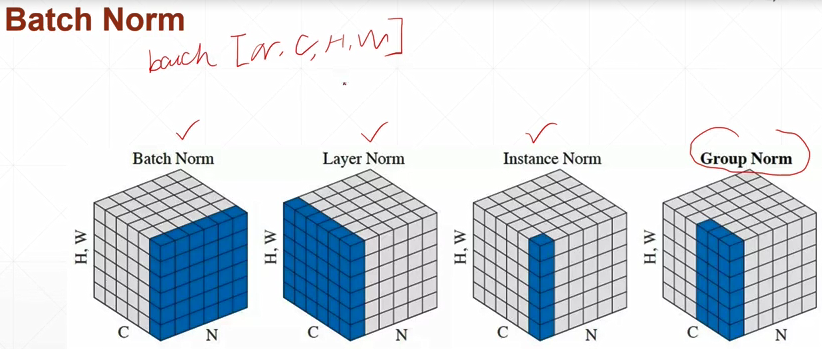
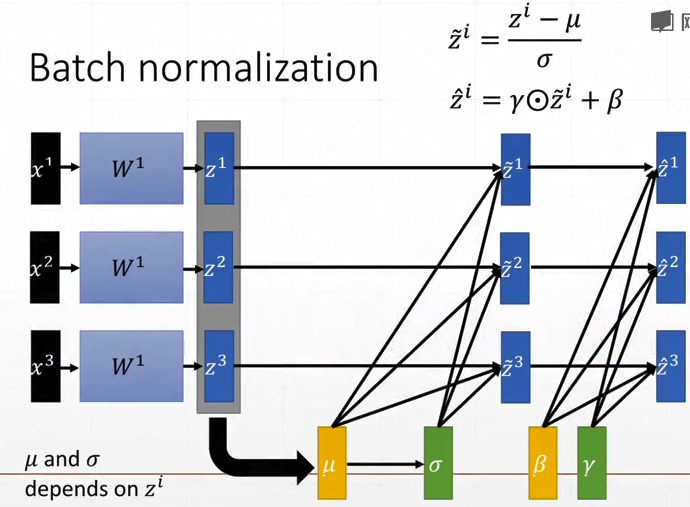
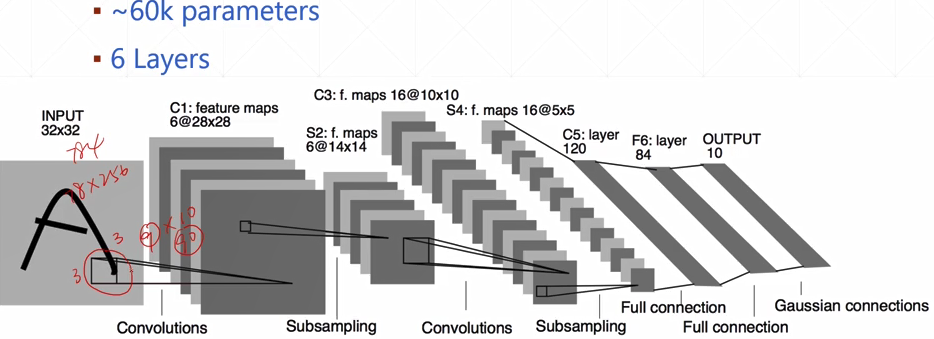
经典卷积网络 LeNet5,AlexNet, VGG, GoogLeNet
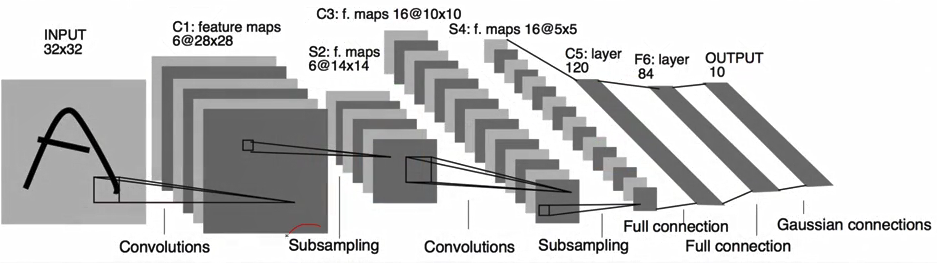
- LeNet-5
99.2%acc
5/6 layers
- AlexNet

- VGG


- GoogLeNet
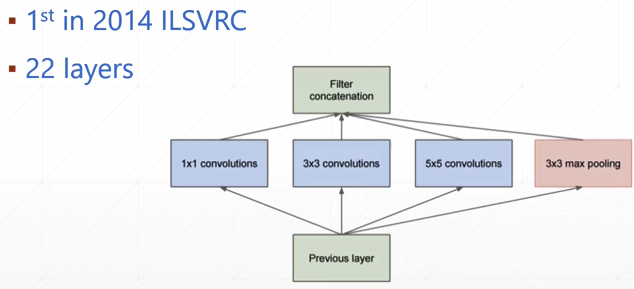

ResNet与DenseNet
直觉:更深层次的网络结构会带来更好的效果
实际上:层数增加以后,每层误差的积累,造成梯度离散或爆炸
人为设置一种机制,使得例如30层的效果再差也不会退化成20层的效果

残差:H(x)-x
- DenseNet
flat:

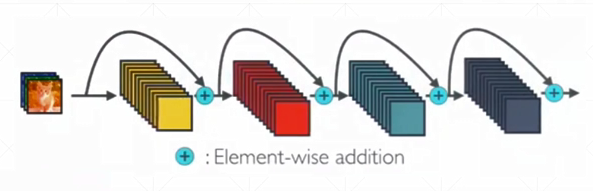
ResNet:
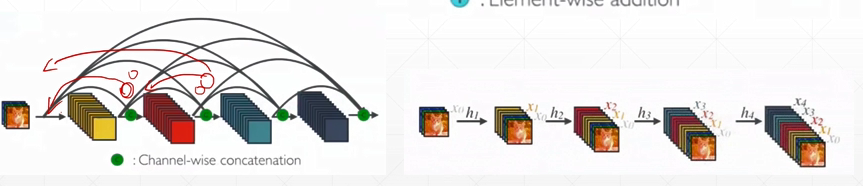
DenseNet:任何一层都有机会跟前面的所有层有接触
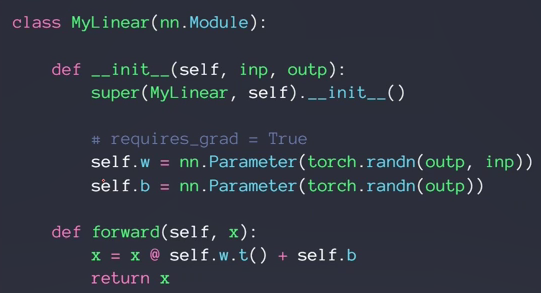
nn.Module模块
所有网络层类的一个辅类

nn.Module可嵌套

功能:
1.nn.Module里提供了大量的神经网络的计算模块

2.container: self.net nn.Sequential

3.parameters
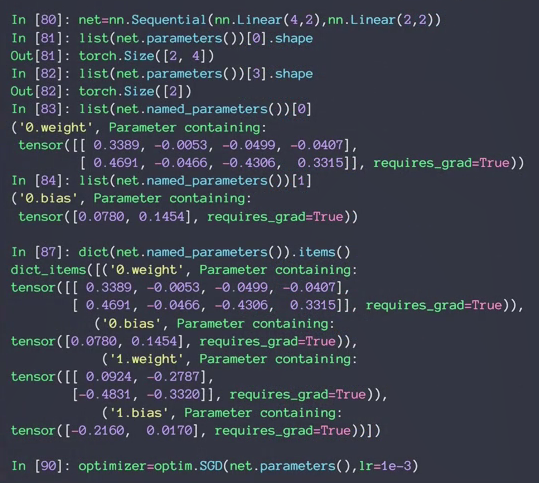
4.modules

直接子节点称为children,所有产生的结点称为modules


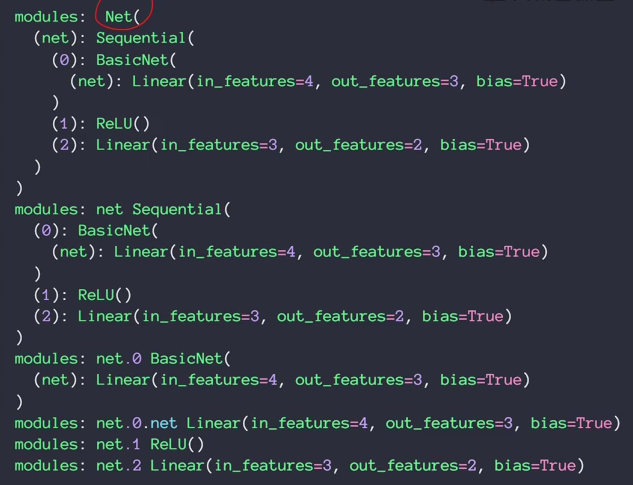
5.to(device)

6.save and load

7.train/test




