数据预处理与特征工程

一、概述

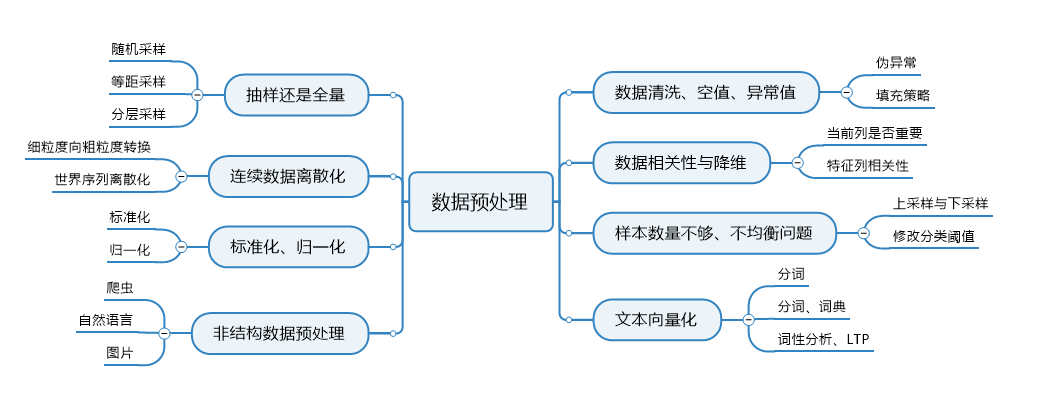
数据预处理是数据分析过程中的重要环节，它直接决定了后期所有数据分析的质量和价值输出。从数据预处理的主要内容看，包括数据清洗、转换、归约、聚合、抽样等8个方向

好多方法既是预处理的方法，也是特征工程的方法，便把两个放在一起讲了。

 

 

 

 

 

二、数据清洗、空值、异常值

在数据清洗过程中，主要处理的是缺失值、异常值、重复值。

所谓清洗，是对数据集通过丢弃、填充、替换、去重等操作。

达到去除异常、纠正错误、补足缺失的目的。

 

2.1 缺失值处理

import numpy as np
import pandas as pd
df = pd.DataFrame(data=np.random.randint(low=1, high=6, size=(6,6)),columns=list('ABCDEF'))
df.iloc[0:2, 0] = np.nan
df.iloc[5, 3] = np.nan
df.iloc[:, 5] = np.nan
print(df)

# 判断缺失值
print(df.isnull())
print(df.isnull().any())                      # 缺失值所在列为True值，所有非缺失值为False
print(df.isnull().all())                      # 某一列所有值为全部为缺失值，则为True

# 填充缺失值
print(df.fillna(value=1))                     # 将缺失值填充为1
print(df.fillna({'A':1.1,'F':0.0}))           # 将A列缺失值填充为1.1；E列缺失值填充为0.0
print(df.fillna(method='pad'))                # 用前面的值替换缺省值
print(df.fillna(method='backfill', limit=1))  # 用后面的值替换缺省值
print(df.fillna(value=df.mean()))             # 所在列平均值填充



# 删除缺失值
print(df.dropna())                               # 直接丢弃有NA的行记录

 

 

 

2.2 重复值处理

df = pd.DataFrame(data={'A':['a','b','a','c'],'B':[3,2,3,2]})
print(df)
# 判断重复数据记录
print(df.duplicated())
# 删除重复值
print(df.drop_duplicates())                         # 默认保留首次出现的数据，需全部重复
print(df.drop_duplicates(['B'], keep='last'))      # 对B列检查是否重复，保留最后一次出现的行

 

2.3 异常值处理

异常数据是数据分布的常态，处于特定分布的区域或者范围之外的数据通常被定义为异常或者”噪音”。

但是在有些业务领域异常数据恰恰正常反映了业务运营结果。我们把数据称为伪异常，此类数据通常不处理。

关键在判断出异常

 

 

三、抽样还是全量

3.1 简单随机抽样

关键是随件找出样本的索引

import random
import numpy as np


data = np.random.randint(low=1, high=5, size=(5,6))

# 随机抽样
list_len = [i for i in range(len(data))]
list_sample = random.sample(list_len, 3)  #从list_len中随机取出三个数
data_sample = data[list_sample]

 

3.2 等距抽样

关键是给数据排序，并等距找出索引

import numpy as np


data = np.random.randint(low=1, high=5, size=(5,6))

# 等距抽样
list_sample = np.linspace(start=0, stop=len(data)-1, num=3) #从[0，len(data)-1]中等距取3个数
data_sample = data[list_sample]

 

 

3.3 分层抽样

分层抽样法也叫类型抽样法。它是从一个可以分成不同子总体（或称为层）的总体中，按规定的比例从不同层中随机抽取样品（个体）的方法。

这种方法的优点是，样本的代表性比较好，抽样误差比较小。缺点是抽样手续较简单随机抽样还要繁杂些。

步骤：1.对样本进行分层，并计算出各层占比

　　　2. 按照比例用用随机抽样或者等距抽样，按比例抽出各层的样本　

 

3.4 整群抽样

整群抽样是指整群地抽选样本单位，对被抽选的各群进行全面调查的一种抽样组织方式。

例如，检验某种零件的质量时，不是逐个抽取零件，而是随机抽若干盒 (每盒装有若干个零件)，对所抽各盒零件进行全面检验。

如果全及总体划分为单位数目相等的R个群，用不重复抽样方法，从R群中抽取r群进行调查

 

 

四、数据相关性与降维

4.1 相关性

 

 

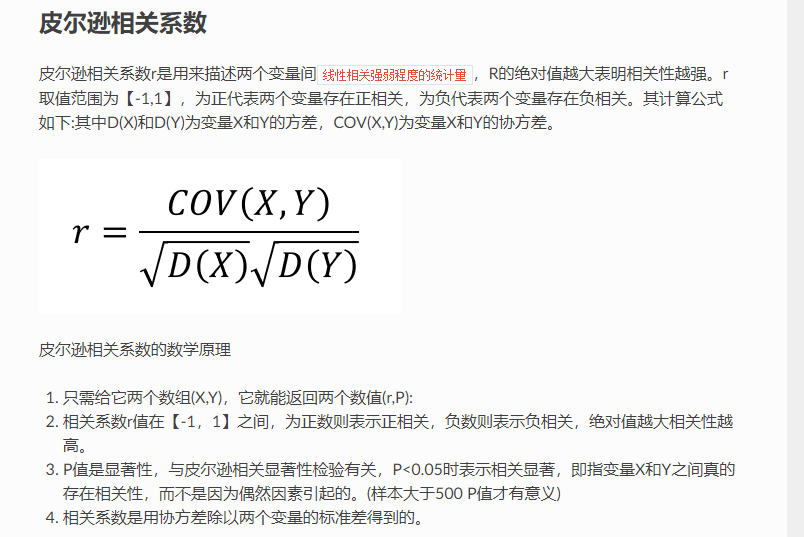
import numpy as np
from scipy.stats import pearsonr
x = np.array([1, 3, 5, 7, 9])
y = np.array([2, 4, 6, 8, 9])
xy = np.array([x,y])

ex = np.average(x)
ey = sum(y)/len(y)
exy = sum(x*y)/len(x)

#协方差
cov_xy = exy-ex*ey            # 详细推导

# 推导尔逊系数
corr = cov_xy/(np.std(x)*np.std(y))
# 使用官方包
corr2 = pearsonr(x, y)[0]
print(corr)
print(corr2)

 

五、连续数据离散化

离散化本质上把无限的空间中有限的个体映射到有限的空间中。

数据离散化操作大多是针对连续数据。处理之后的数据值域分布将从连续数据变为离散数据。

 

5.1 时间序列离散化

如果时间序列唯一，可以考虑用作索引。

import numpy as np
import pandas as pd


def group_num(val):
    if val <30:
        return 'A'
    elif val < 60:
        return 'B'
    else:
        return 'C'


data_date = pd.date_range(start='2022-01-01', periods=365)
data_value = np.random.randint(low=1,high=100,size=365)
df = pd.DataFrame(data=data_value, index=data_date, columns=['value'])   # 以时间序列为索引
df['weekday'] = [i.weekday() for i in df.index]                          # 对时间序列离散化
df['degree'] = df['value'].map(group_num)                                # 对数值进行离散化
print(df)

 

 

 

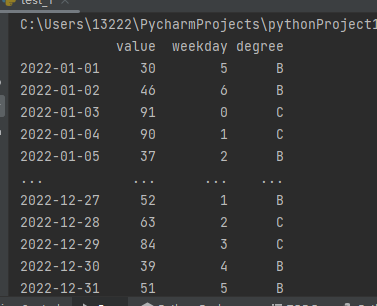
5.2 采用map实现离散化

上面代码中已经使用map来对数值进行分组，注意分组函数不要加括号。

 

 

六、 归一化与标准化

6.1 归一化

6.1.1 含义

 

 

 

6.1.2 代码展示

# preprocessing包下面的__init__.py文件导入了MinMaxScaler类
from sklearn.preprocessing import MinMaxScaler
# 本质上就是调用了前面的公式,可以自己指定max,min范围默认0~1之间
mm = MinMaxScaler(feature_range=(0, 1))
data = mm.fit_transform([[1, 1, 1, 1],
                         [2, 5, 10, 11],
                         [5, 26, 21, 3]])
print(data)

 

 

 

 

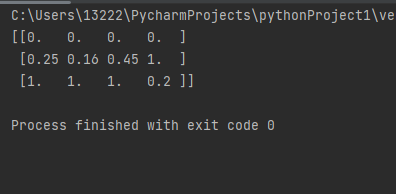
6.1.3 缺点

1. 根据公式，当前待计算的x为当前列最大值时,最终归一化为1，待计算的x为当前列最小值时,最终归一化为0对异常点的包容性差 (如果异常点影响了最大值或者最小值，则会造成整体数值计算偏差)，因此这种方式稳定性较差，适合比较精确数据模型

2. 对异常点的包容性差 (如果异常点影响了最大值或者最小值，则会造成整体数值计算偏差)，因此这种方式稳定性较差，适合比较精确数据模型

 

6.2 标准化

6.2.1 含义

 

 

6.2.2 代码展示

 

 

 

from sklearn.preprocessing import StandardScaler
std= StandardScaler()
data = std.fit_transform([[1, 1, 1, 1],
                         [2, 5, 10, 11],
                         [5, 26, 21, 3]])
print(data)

 

 

  

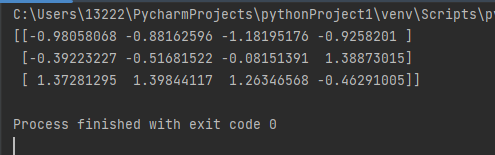
6.2.3 对比归一化

1. 对于归一化来说：如果出现了异常点，影响了最大值与最小值，那么结果显然会发生改变
2. 对于标准化来说：如果出现异常点，由于具有一定数据量，少量的异常点对于平均值的影响并不大，从而方差改变较小
3. 方差可以用来衡量与中心偏离的程度，用来衡量一批数据的波动大小,方差越大，说明数据的波动越大，越不稳定
4. 如果var方差为0，则说明某特征列的值都相同,那么在后续进行此机器学习时此特征列可以忽略

 

6.2.4 应用场景

数据归一与标准化的理由是，消除属性之间的不同量纲引起的误差，加快运算速度，提升运算的准确性

1. 归一化只是所有的数据换了一个尺度而已。对于线性回归，所有的数据换一个尺度，对应求出的线性回归的系数，也跟着这个尺度变化一下而已，不会影响预测的准确率
2. 有一些算法无需归一化，有一些算法需要。kNN是典型的需要进行归一化处理的算法
3. 整体而言，对于大多数机器学习算法，对数据进行一次归一化，都是没有坏处的

 

 

七、 样本数量不够、不均衡问题

参考博客：https://blog.csdn.net/Scc_hy/article/details/84190080

 

八、 文本向量化

8.1 OneHotEncode独热编码

对于离散的特征基本就是按照one-hot（独热）编码，该离散特征有多少取值，就用多少维来表示该特征

from sklearn.preprocessing import OneHotEncoder
import warnings
warnings.filterwarnings('ignore')
enc = OneHotEncoder(sparse=False)
result = enc.fit_transform([['男', '汉', '刘邦'],
                            ['女', '楚', '虞姬'],
                            ['男', '秦', '章邯'],
                            ['女', '汉', '吕雉']])
print(enc.get_feature_names())
print('*'*50)
print(result)
print('*'*50)
print(enc.inverse_transform(result))    # 将向量化解析为字符串
print('*'*50)
# 这里使用一个新的数据来测试
result = enc.transform([['男', '楚', '章邯']])
print(result)

 

 

 

 

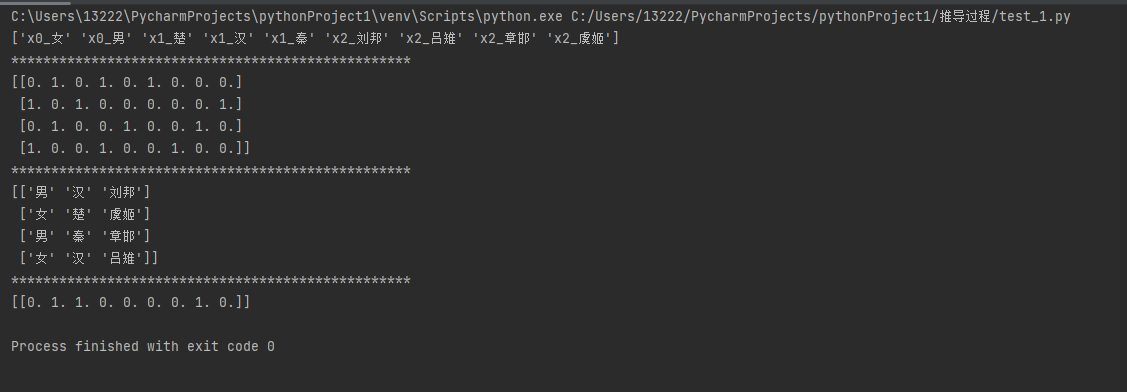
优点：

使用one-hot编码，将离散特征的取值扩展到了欧式空间，离散特征的某个取值就对应欧式空间的某个点；

将离散特征通过one-hot编码映射到欧式空间，是因为，在回归，分类，聚类等机器学习算法中，特征之间距离的计算或相似度的计算是非常重要的，而我们常用的距离或相似度的计算都是在欧式空间的相似度计算。

对离散型特征进行one-hot编码是为了让距离的计算显得更加合理

缺点：

当类别的数量很多时，特征空间会变得非常大。在这种情况下，一般可以用PCA来减少维度。而且One-Hot + PCA这种组合在实际中也非常有用。

但如果特征项不是为了计算距离，那么就没必要进行one-hot编码。

仅仅只需要把非数值转化为数值型即可。此时可以采用LabelEncoder

 

8.2 TF-IDF推导

8.2.1 含义

 

 

 

8.2.2 推导

import numpy as np
from collections import Counter
import jieba.analyse
jieba.setLogLevel(jieba.logging.INFO)


str1 = '中国 日本 美国 新加坡 加拿大 美国 中国'
str2 = '美国 新加坡 加拿大'
str3 = '日本 美国'
str4 = '日本 美国 韩国 德国 法国 英国'
str5 = '日本 美国 英国 意大利 西班牙'
str6 = '英国 意大利 西班牙 韩国 德国 法国 英国 '


data_content = [str1, str2, str3,str4,str5,str6]
doc_count = len(data_content)
idf_dic = {}  # 存储idf的值
data_list = []

# 统计包含该词的文档数
for i in data_content:
    str_i = list(set(i.split()))
    for j in str_i:
        data_list.append(j)
data_dic =dict(Counter(data_list))

for k,v in data_dic.items():
    # idf = log (语料库总文档数量/包含该词的文档数)
    p = np.log(doc_count / (v + 1))
    idf_dic[k] = round(p,7)




# 要计算词频的文章
content = "中国 英国 意大利 美国 中国"
# 获取当前文章的词的列表
words = content.split(' ')
# 统计某个词在文章中出现的次数
temp = Counter(words)
print(temp['中国'], idf_dic['中国'])
print("中国:TF-IDF:",temp['中国'] / len(words) * idf_dic['中国'])
print("美国:TF-IDF:",temp['美国'] / len(words) * idf_dic['美国'])




# 构建自己的语料库
with open(file="../data/wdic.txt", mode="w",encoding="utf-8") as f:
    for k, v in idf_dic.items():
        f.write(k + ' ' + str(v) + "\n")  # 把idf写入到txt文件中

# 利用语料库
jieba.analyse.set_idf_path("../data/wdic.txt")
# 如果语料库中不存在的词,也会有一个值，但是怎么来的没看懂源码，也没找到相关的文章
# jieba.analyse.set_stop_words("../data/stop_words.txt")
res = jieba.analyse.tfidf("中国 英国 意大利 美国 中国 ",withWeight=True)
print(res)

 

 

 

 

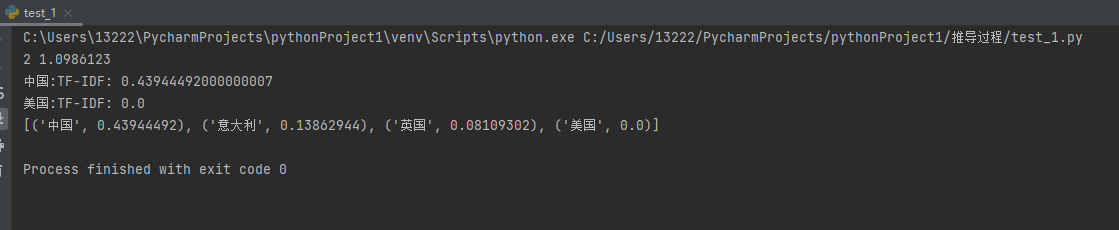
8.3 TfidfVectorizer推导

8.3.1 含义

Sklearn框架可以使用TfidfVectorizer来实现文本特征提取。但是它的TF-IDF公式与之前的jieba公式略有不同。

1. 平滑版公式为：tf−idf = tf(t,d)∗idf(t)
2. tf(t,d) 表示在文本d中词项t出现的词数 (无需在除文章总词数)
3. df(t)= log((1 + 语料库文档总数) /（1 + 包含该词的文档数)) + 1

注意：TF-IDF只是考虑了词项在所有文本间的分布特性，这里并不涉及词性，因此TfidfVectorizer的输入也不需要提供词性信息。

 

8.3.2  推导

# 导入TfidfVectorizer
from sklearn.feature_extraction.text import TfidfVectorizer
import warnings
warnings.filterwarnings('ignore')
# 实例化tf实例
tv = TfidfVectorizer(use_idf=True, smooth_idf=True, norm=None)
# 输入训练集矩阵，每行表示一个文本

train_1 = '刘邦 韩信 刘邦'
train_2 = '刘邦 刘邦 张良'
train_3 = '刘邦 章邯'
train_4 = '龙且 项羽 刘邦'
test_1 = '项羽 刘邦 韩信'
test_2 = '刘邦 张良 韩信 萧何'

train = [train_1, train_2, train_3, train_4]
test = [test_1, test_2]
# 训练过程就是构建语料库的过程,后续计算IDF需要语料库

# 训练集
tv_fit = tv.fit(train)
# 查看一下构建的词汇表
X_train = tv.transform(train)
X_test = tv.transform(test)

print('tv.vocabulary_:\n', tv.vocabulary_)
print('tv.get_feature_names:\n', tv.get_feature_names())
print('X_train.toarray:\n', X_train.toarray())
print('X_test.toarray: \n', X_test.toarray())
print('X_train: \n', X_train)
print('X_test: \n', X_test)

 

 

 

 

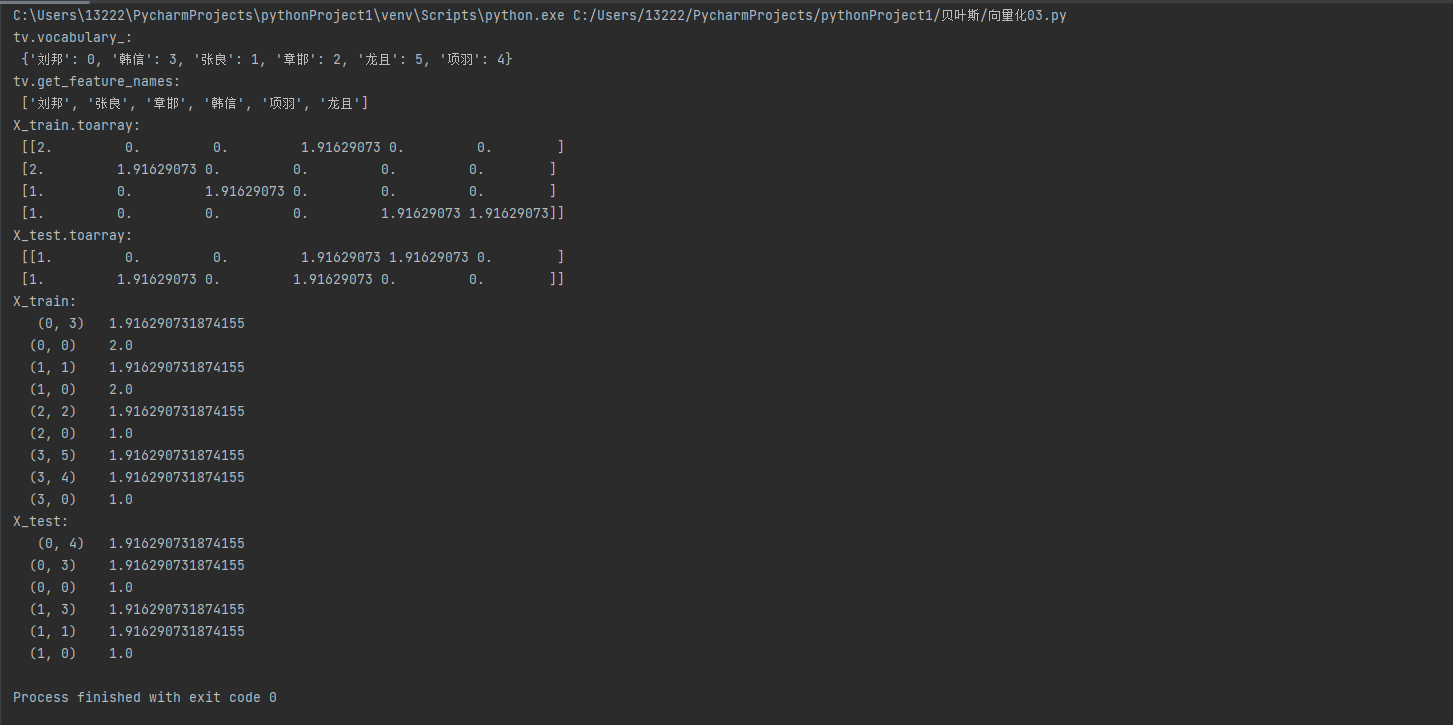
tv.vocabulary_:

文本各个词汇按首字母的位置是几号，用vocabulary_函数,得到 {'刘邦': 0, '韩信': 3, '张良': 1, '章邯': 2, '龙且': 5, '项羽': 4}。

tv.get_feature_names：

这个文本有哪些词汇，用get_feature_names()函数,按照水平排好了。

X_train.toarray：

 

 

 

 

 

以刘邦在X_train_1中的数为例

tf = 2 

idf = log((4+1)/(4+1))+1 = 1

结果为：tf*idf = 2*1=2

 

 X_test.toarray：

同X_train.toarry

以项羽在test_1中为例

tf = 1

idf = log((4+1)/(1+1)) = 1.91629

结果为 tf*idf = 1.91629

萧何因为不在语料库中所以不显示。

 

 X_train

 

 

 

以刘邦在train_1为例：

train_1在是第一个句子，索引为0

刘邦在vocabulary_中的值为0，

tf(t,d)*idf(t) = 2

于是（0,0） 2.0 代表刘邦

 

X_test

 同X_train

 

 

8.4 CountVectorizer推导

参考：https://blog.csdn.net/qq_43840793/article/details/115960115

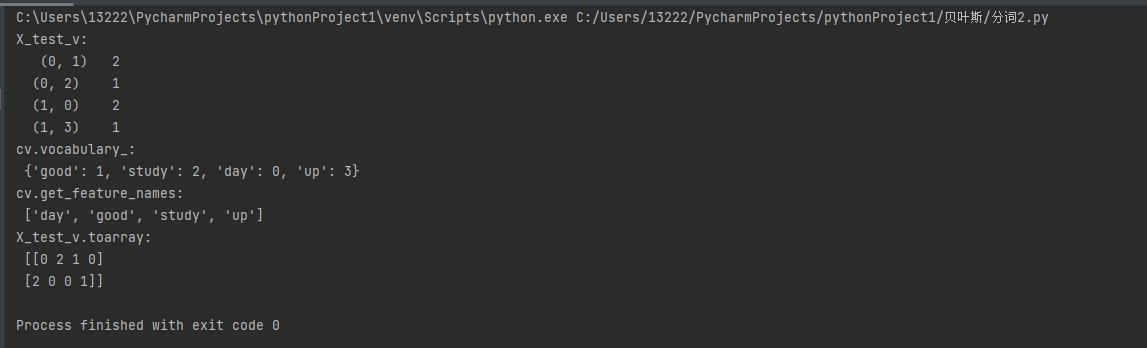
from sklearn.feature_extraction.text import CountVectorizer
import warnings
warnings.filterwarnings('ignore')

X_test = ['good good study stop', 'day day up stop']
cv = CountVectorizer(stop_words=['stop'])
X_test_v = cv.fit_transform(X_test)
print('X_test_v: \n', X_test_v)
print('cv.vocabulary_:\n', cv.vocabulary_)
print('cv.get_feature_names:\n', cv.get_feature_names())
print('X_test_v.toarray:\n', X_test_v.toarray())

 

 

 

 

参数：

可以参考：https://zhuanlan.zhihu.com/p/37644086

stop_words：停用词

 

X_test_v 推导：

首先给各个自排序（英文是按照字母进行排序），如下表

 

 

 

转化一下

 

 

 

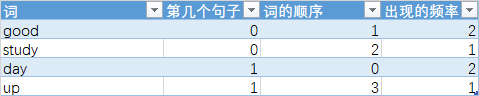
表中的三个数字便是X_test_v

 

 

 

 

 

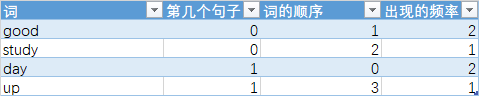
vocabulary_推导:

文本各个词汇按首字母的位置是几号，用vocabulary_函数,得到 {'good': 1, 'study': 2, 'day': 0, 'up': 3}。

 day的首字母是d,所以排在第1位。

 

cv.get_feature_names推导：

这个文本有哪些词汇，用get_feature_names()函数

vocabulary推导: 

 

 

第1个句子的词频向量  [0 2 1 0]

第2个句子的词频向量 [2 0 0 1]

 

相似度

即两个句子的余弦值

 

 

 

 

 

 

 

 

 

 

 

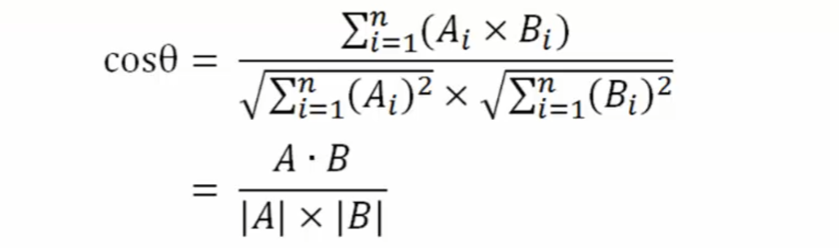
九、 非结构数据预处理

还未理解o(╥﹏╥)o