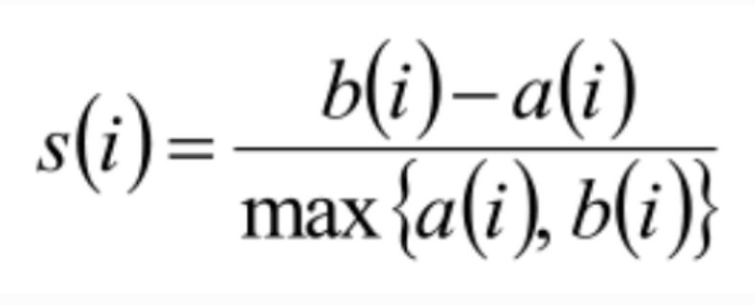机器学习常用评判依据
一、概述
需要对推算结果与真实结果进行评判,主要有下属各种。

二、方差与标准差
2.1 含义

2.2 Pyhton展示
import numpy as np y_true = np.array([1.0, 2.0, 3.0, 4.0]) var = np.var(y_true) std = np.std(y_true) print(f'var:{var}') # var:1.25 print(f'std:{std}') # std:1.118033988749895
三、绝对值误差
3.1 含义
单个预测值与真实值之间的误差,此误差通过绝对值然后再求和求平均
3.2 Python展示
import numpy as np from sklearn.metrics import mean_absolute_error y_true = np.array([1.0, 2.0, 3.0, 4.0]) y_pred = np.array([0.0, 3.0, 5.0, 7.0]) diff = y_true-y_pred # 绝对值误差 mae = mean_absolute_error(y_true, y_pred) mae2 = np.average(np.abs(diff)) print(f'mae:{mae}, mae2:{mae2}') # mae:1.75, mae2:1.75
四 均方误差与均方根误差
4.1 含义

4.2 Python展示
import numpy as np from sklearn.metrics import mean_squared_error y_true = np.array([1.0, 2.0, 3.0, 4.0]) y_pred = np.array([0.0, 3.0, 5.0, 7.0]) diff = y_true-y_pred # 均方误差 mse = mean_squared_error(y_true, y_pred) mse2 = np.average(np.square(diff)) print(f'mse:{mse}, mse2:{mse2}') # mse:3.75, mse2:3.75
五、拟合度
5.1 含义
拟合度检验是对已制作好的预测模型进行检验,比较它们的预测结果与实际发生情况的吻合程度。通常是对数个预测模型同时进行检验,选其拟合度较好的进行试用。
常用的拟合度检验方法有:剩余平方和检验、卡方(c2)检验和线性回归检验等。拟合度,也就是“R-squared”。

也就是 R2 = 1- 均方误差/方差
5.2 Python展示
import numpy as np from sklearn.metrics import r2_score y_true = np.array([1.0, 2.0, 3.0, 4.0]) y_pred = np.array([0.0, 3.0, 5.0, 7.0]) # r2_score r2 = r2_score(y_true,y_pred) print(r2) # -2.0
六、精确率、召回率 、准确率 、F1分数
准确率->accuracy, 精确率->precision. 召回率-> recall. 三者很像,但是并不同,简单来说三者的目的对象并不相同。
大多时候我们需要将三者放到特定的任务环境中才会更加明显的感觉到三者的差异。
6.1 混淆矩阵
- True Positive(真正, TP):将正类预测为正类数
- True Negative(真负 , TN):将负类预测为负类数
- False Positive(假正, FP):将负类预测为正类数 →→ 误报 (Type I error)
- False Negative(假负 , FN):将正类预测为负类数 →→ 漏报 (Type II error)
6.2 精确率
实际上非常简单,精确率是对我们的预测结果而言的指标,它表示的是预测为正的样本中有多少是真正的正样本。
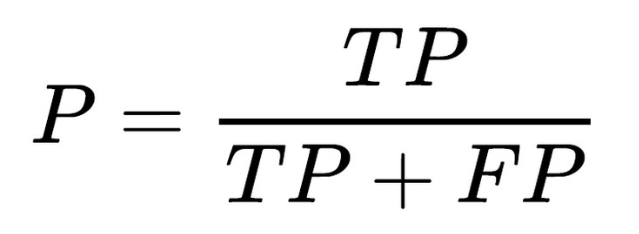
6.3 召回率
召回率是针对我们原来的样本而言的,它表示的是样本中的正例有多少被预测正确了。那也有两种可能,一种是把原来的正类预测成正类(TP),另一种就是把原来的正类预测为负类(FN)
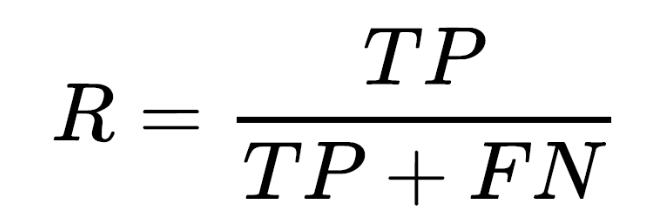
6.4 准确率
模型预测正确的结果所占的比例
准确率(accuracy)=(TP+TN)/(TP+FN+FP+TN)
6.5 F1-Score
数学上定义为精确率和召回率的调和均值,它也是在评估这类样本分类数据不平衡问题时,所着重的标准
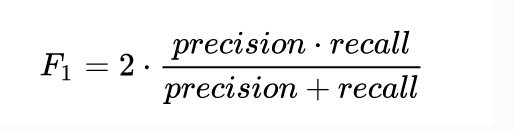
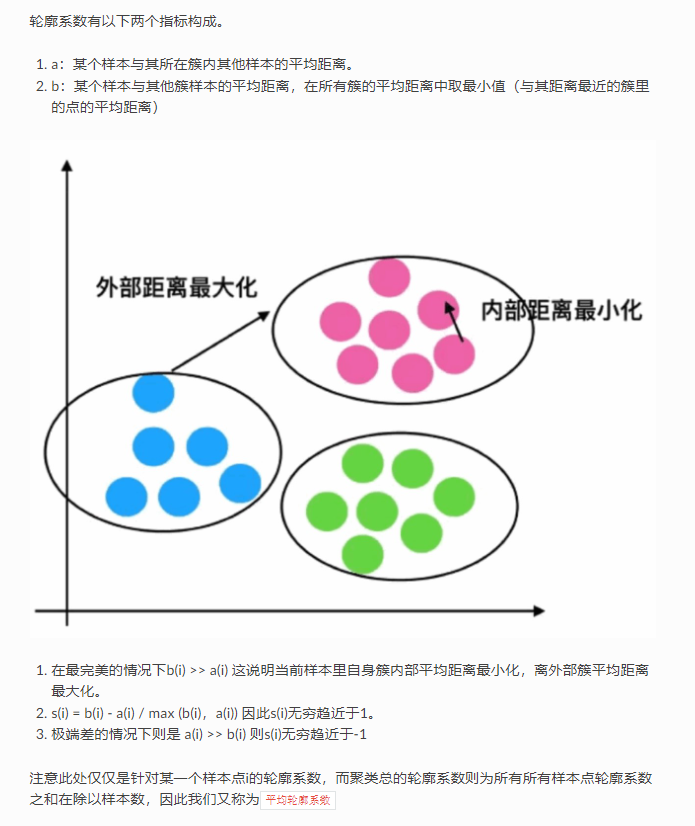
七、 轮廓系数
轮廓系数作为聚类性能的评估指标。
轮廓系数取值范围为[-1,1],取值越接近1则说明聚类性能越好,相反,取值越接近-1则说明聚类性能越差。轮廓系数的公式如下: