二叉树的各种遍历

二叉树，一棵树最多有两个叉，就像一个最多生两个孩子

 

二叉树结点

//二叉树节点
public class BinaryTreeNode {
    private int data;
    private BinaryTreeNode left;
    private BinaryTreeNode right;

    public BinaryTreeNode() {}

    public BinaryTreeNode(int data, BinaryTreeNode left, BinaryTreeNode right) {
        super();
        this.data = data;
        this.left = left;
        this.right = right;
    }

    public int getData() {
        return data;
    }

    public void setData(int data) {
        this.data = data;
    }

    public BinaryTreeNode getLeft() {
        return left;
    }

    public void setLeft(BinaryTreeNode left) {
        this.left = left;
    }

    public BinaryTreeNode getRight() {
        return right;
    }

    public void setRight(BinaryTreeNode right) {
        this.right = right;
    }
}

　　

前序递归遍历算法：访问根结点-->递归遍历根结点的左子树-->递归遍历根结点的右子树

 中序递归遍历算法：递归遍历根结点的左子树-->访问根结点-->递归遍历根结点的右子树

 后序递归遍历算法：递归遍历根结点的左子树-->递归遍历根结点的右子树-->访问根结点

 

前序遍历（Preorder Traversal (DLR)），是二叉树遍历的一种，也叫做先根遍历、先序遍历、前序周游，可记做根左右。
前序遍历首先访问根结点然后遍历左子树，最后遍历右子树。

 

中序遍历（Inorder Traversal (LDR)）是二叉树遍历的一种，也叫做中根遍历、中序周游。
中序遍历首先遍历左子树，然后访问根结点，最后遍历右子树。

后序遍历（Postorder Traversal (LRD)）是二叉树遍历的一种，也叫做后根遍历、后序周游，可记做左右根。后序遍历有递归算法和非递归算法两种。
先左后右再根，即首先遍历左子树，然后遍历右子树，最后访问根结点。

public class BinaryTree2 {
    //前序遍历递归的方式
    public void preOrder(BinaryTreeNode root){
        if(null!=root){
            System.out.print(root.getData()+"\t");
            preOrder(root.getLeft());
            preOrder(root.getRight());
        }
    }


    //中序遍历采用递归的方式
    public void inOrder(BinaryTreeNode root){
        if(null!=root){
            inOrder(root.getLeft());
            System.out.print(root.getData()+"\t");
            inOrder(root.getRight());
        }
    }


    //后序遍历采用递归的方式
    public void postOrder(BinaryTreeNode root){
        if(root!=null){
            postOrder(root.getLeft());
            postOrder(root.getRight());
            System.out.print(root.getData()+"\t");
        }
    }



    //层序遍历
    public void levelOrder(BinaryTreeNode root){
        BinaryTreeNode temp;
        Queue<BinaryTreeNode> queue=new LinkedList<BinaryTreeNode>();
        queue.offer(root);
        while(!queue.isEmpty()){
            temp=queue.poll();
            System.out.print(temp.getData()+"\t");
            if(null!=temp.getLeft())
                queue.offer(temp.getLeft());
            if(null!=temp.getRight()){
                queue.offer(temp.getRight());
            }
        }
    }

    public static void main(String[] args) {
        BinaryTreeNode node10=new BinaryTreeNode(10,null,null);
        BinaryTreeNode node8=new BinaryTreeNode(8,null,null);
        BinaryTreeNode node9=new BinaryTreeNode(9,null,node10);
        BinaryTreeNode node4=new BinaryTreeNode(4,null,null);
        BinaryTreeNode node5=new BinaryTreeNode(5,node8,node9);
        BinaryTreeNode node6=new BinaryTreeNode(6,null,null);
        BinaryTreeNode node7=new BinaryTreeNode(7,null,null);
        BinaryTreeNode node2=new BinaryTreeNode(2,node4,node5);
        BinaryTreeNode node3=new BinaryTreeNode(3,node6,node7);
        BinaryTreeNode node1=new BinaryTreeNode(1,node2,node3);

        BinaryTree2 tree=new BinaryTree2();
        //采用递归的方式进行遍历
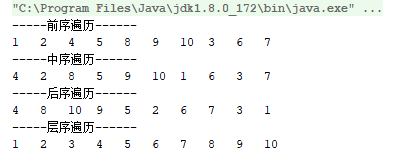
        System.out.println("-----前序遍历------");
        tree.preOrder(node1);
        System.out.println();


        //采用递归的方式进行遍历
        System.out.println("-----中序遍历------");
        tree.inOrder(node1);
        System.out.println();


        //采用递归的方式进行遍历
        System.out.println("-----后序遍历------");
        tree.postOrder(node1);
        System.out.println();


        //采用递归的方式进行遍历
        System.out.println("-----层序遍历------");
        tree.levelOrder(node1);
        System.out.println();
    }
}

 

　采用非递归的方式

public class BinaryTree {

    //前序遍历非递归的方式
    public void preOrderNonRecursive(BinaryTreeNode root){
        Stack<BinaryTreeNode> stack=new Stack<BinaryTreeNode>();
        while(true){
            while(root!=null){
                System.out.print(root.getData()+"\t");
                stack.push(root);
                root=root.getLeft();
            }
            if(stack.isEmpty()) break;
            root=stack.pop();
            root=root.getRight();
        }
    }


    //中序遍历采用非递归的方式
    public void inOrderNonRecursive(BinaryTreeNode root){
        Stack<BinaryTreeNode> stack=new Stack<BinaryTreeNode>();
        while(true){
            while(root!=null){
                stack.push(root);
                root=root.getLeft();
            }
            if(stack.isEmpty())break;
            root=stack.pop();
            System.out.print(root.getData()+"\t");
            root=root.getRight();
        }
    }


    //后序遍历采用非递归的方式
    public void postOrderNonRecursive(BinaryTreeNode root){
        Stack<BinaryTreeNode> stack=new Stack<BinaryTreeNode>();
        while(true){
            if(root!=null){
                stack.push(root);
                root=root.getLeft();
            }else{
                if(stack.isEmpty()) return;

                if(null==stack.lastElement().getRight()){
                    root=stack.pop();
                    System.out.print(root.getData()+"\t");
                    while(root==stack.lastElement().getRight()){
                        System.out.print(stack.lastElement().getData()+"\t");
                        root=stack.pop();
                        if(stack.isEmpty()){
                            break;
                        }
                    }
                }

                if(!stack.isEmpty())
                    root=stack.lastElement().getRight();
                else
                    root=null;
            }
        }
    }


    public static void main(String[] args) {
        BinaryTreeNode node10 = new BinaryTreeNode(10, null, null);
        BinaryTreeNode node8 = new BinaryTreeNode(8, null, null);
        BinaryTreeNode node9 = new BinaryTreeNode(9, null, node10);
        BinaryTreeNode node4 = new BinaryTreeNode(4, null, null);
        BinaryTreeNode node5 = new BinaryTreeNode(5, node8, node9);
        BinaryTreeNode node6 = new BinaryTreeNode(6, null, null);
        BinaryTreeNode node7 = new BinaryTreeNode(7, null, null);
        BinaryTreeNode node2 = new BinaryTreeNode(2, node4, node5);
        BinaryTreeNode node3 = new BinaryTreeNode(3, node6, node7);
        BinaryTreeNode node1 = new BinaryTreeNode(1, node2, node3);

        BinaryTree tree = new BinaryTree();

        System.out.println("-----前序遍历------");
        //采用非递归的方式遍历
        tree.preOrderNonRecursive(node1);
        System.out.println();


        System.out.println("-----中序遍历------");
        //采用非递归的方式遍历
        tree.inOrderNonRecursive(node1);
        System.out.println();

        System.out.println("-----后序遍历------");
        //采用非递归的方式遍历
        tree.postOrderNonRecursive(node1);
        System.out.println();

    }
}