20182333 2019-2020-1 《数据结构与面向对象程序设计》第十周学习总结
20182333 2019-2020-1 《数据结构与面向对象程序设计》第十周学习总结
教材学习内容总结
图
- 与树类似,图由结点和这些结点之间的连接构成。
- 顶点(vertice):就是结点。
- 边(edge):就是这些结点连接起来的线段。
- 路径(path):图中的一系列边,每条边连通两个顶点。
- 路径的长度(length):是该路径中边的条数(或者是顶点数减去1)。
- 环路(cycle):一种首结点和末结点相同且没有重边的路径。没有环路的图称为无环的(acyclic)。
- 完全图(complete graph):含有最多条边的无向图
无向图
-
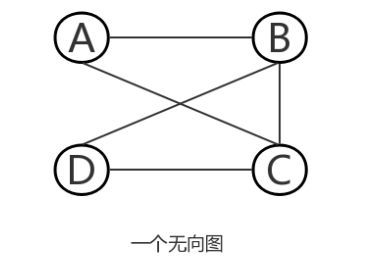
边没有方向的图称为无向图。
-
无向图中,表示边的顶点对是无序的,例如,标记顶点A,B,C,D,一条边可以表示为(A,B)。无向图表示顶点对是无序的,所以边(A,B)意味着A和B之间的连接是双向的,在一个无向图中,(A,B)和(B,A)所代表的边的含义完全一样。
-
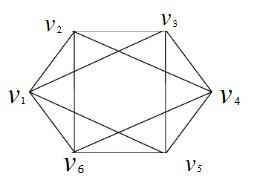
含有最多条边的无向图称为完全图:Edges=(n-1)*n/2.
-
如果无向图中任意两个顶点间都有路径,则无向图称为连通的。
-
路径是连接图中两个顶点的边的序列,路径长度为路径所含边的数目(顶点个数减一)
-
第一个顶点和最后一个顶点是同一个顶点且没有重复边的路径,称为一个环。
-
如果图中两个顶点之间有边连接,则称这两个顶点是邻接的(邻居),自己连接到自己的边称为自循环或悬挂。
有向图
-
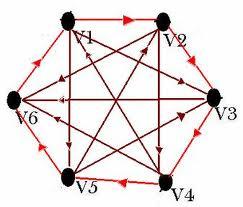
如果给图的每条边规定一个方向,那么得到的图称为有向图,其边也称为有向边。在有向图中,与一个节点相关联的边有出边和入边之分,而与一个有向边关联的两个点也有始点和终点之分。
-
顶点是有序对的图称为有向图,有向图的每条边都带有一个移动方向,这个方向有顶点的顺序指定,所以(A,B)表示只允许从A移动到B,但不允许另一个方向的移动。
-
树就是图,树的大部分工作是针对有向树。有向树是一个有向图。

- 如上图:a是强连通,b是单向连通,c是弱连通。
带权图
-
每条边都对应一个权值的图成为带权图,有时也成为网络。
-
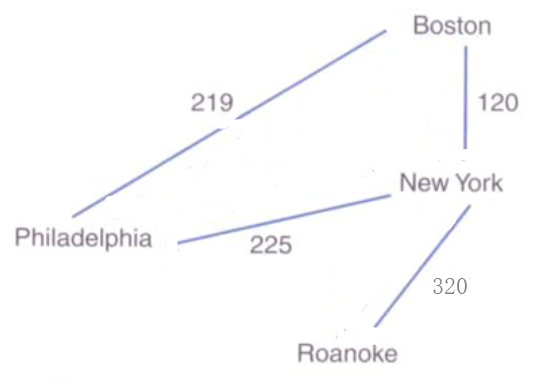
无向带权图
-
有向带权图

常用的图的算法
-
图的遍历:
- 广度优先遍历:从一个顶点开始,辐射状地优先遍历其周围较广的区域。就如同树中的层次遍历。
- 深度优先遍历:图的深度优先搜索,类似于树的先序遍历,所遵循的搜索策略是尽可能“深”地搜索图。就如同树中的前序遍历。
-
测试连通性:
- 连通性:图中的任意两个顶点之间都存在一条路径,则认为这个图是连通的。
- 测试方法:
- 从任意结点开始的广度优先遍历中得到的顶点数等于图中所含顶点数。
-
生成树(spanning tree):包含图中所有顶点及图中部分边的一棵树。
-
最小生成树(minimum spanning tree):所含边权值之和小于其他生成树的边的权值之和。
- Prim算法和Kruskal算法
-
判定最短路径:
- 判定起始顶点和目标顶点之间是否存在最短路径(两个顶点之间边数最少的路径)。
- 在加权图中找到最短路径。(Dijkstra算法)
-
图的实现策略:
- 邻接列表:用一种类似于链表的动态结点来存储每个结点带有的边。这种链表称为邻接列表。
- 邻接矩阵:用一种叫邻接矩阵的二维数组来表示任意两个顶点的交接情况。
- 无向图的邻接矩阵一定是对称的,有向图的邻接矩阵不一定对称。
- 十字链表法
教材学习中的问题和解决过程
-
问题1:图的遍历与树的遍历有什么区别?
-
问题1解决方案:树是有序的,图是无序的。图有两种遍历方法,一种是广度优先遍历,另一种是深度优先遍历。对于树来说,它的广度优先遍历就是层序遍历,深度优先遍历就是先序遍历。
-
问题2:无向图中的连通和完全之间的关系是什么。
-
问题2解决方案:
1.完全是任意两个顶点之间都会有一条边。 2.连通是任意两个顶点之间都存在一条路径。 3.完全的一定连通。 -
问题3:如何理解广度、深度优先遍历?
-
问题3解决方案:
-
广度优先遍历:左看看、又看看,雨露均沾。
-
伪代码:
1. 初始化队列:visited[n] = 0 2. 访问顶点:visited[v] = 1 3. 顶点v加入队列 4. 循环: while(队列是否为空) v = 队列头元素 w = v的第一个邻接点 while(w存在) if(如果w未访问) visited[w] = 1; 顶点w加入队列 w = 顶点v的下一个邻接点- 深度优先遍历:一条路走到底。
- 伪代码:
1. 访问数组初始化:visited[n] = 0 2. 访问顶点:visited[v] = 1 3. 取v的第一个邻接点w; 4. 循环递归: while(w存在) if(w未被访问过) 从顶点w出发递归执行; w = v的下一个邻接点; -
代码调试中的问题和解决过程
- 问题1:如何判断图的的一个图是否连通?
- 问题1解决方案:
- 如果是连通的,当且仅当使用广度优先遍历中的定点数等于图中的顶点数。
- 因此,我们只要定义一个int值,当每遍历一个顶点,就加一。遍历完成后,看该值是否等于顶点数就OK啦。
- 代码实现
public boolean isConnected()
{
boolean result = true;
for(int i=0;i<numVertices;i++){
int temp=0;
temp=getSizeOfIterator(this.iteratorBFS(vertices[i]));
if(temp!=numVertices)
{
result = false;
break;
}
}
return result;
}
代码托管

上周考试错题总结
上周没有考试,所以没有错题。
点评过的同学博客和代码
-
本周结对学习情况
-
上周博客互评情况
其他(感悟、思考等,可选)
本周主要学习了图的知识,例如如何画邻接矩阵、十字链表和邻接链表。如何计算图的广度优先遍历和深度优先遍历。还有用Prim算法和Kruskal算法计算最小生成树等等。
学习进度条
| 代码行数(新增/累积) | 博客量(新增/累积) | 学习时间(新增/累积) | 重要成长 | |
|---|---|---|---|---|
| 目标 | 10000行 | 30篇 | 400小时 | |
| 第一周 | 56/56 | 2/2 | 20/20 | 主要学会了简单的操作Linux以及如何编写简单的java程序并将它上传到码云 |
| 第二、三周 | 331/407 | 3/5 | 23/43 | 学会了一些类和程序包的使用,也明白了C语言和Java在有些地方的区别 |
| 第四周 | 595/1002 | 2/7 | 20/60 | 学会了IDEA以及用IDEAgit码云,也学会了TDD测试 |
| 第五周 | 1621/2623 | 2/9 | 17/77 | 见识了服务器与用户链接的代码,也学习了继承的一些知识。 |
| 第六周 | 1770/4393 | 1/10 | 22/99 | 学习了多态以及与接口和继承的关系,还有就是对异常的学习和处理异常的方法以及自定义一个异常 |
| 第七周 | 1747/6140 | 3/13 | 23/122 | 学习了渐进复杂度的计算,栈和队列的学习,分别用数组和链表实现队列 |
| 第八周 | 384/6524 | 1/14 | 20/142 | 学习了一些查找和排序的算法,也学会了计算ASL |
| 第九周 | 1895/8419 | 3/17 | 22/164 | 学习了树的四种遍历,和怎样根据已知序列求未知序列等等 |
| 第十周 | 1946/10365 | 3/20 | 22/183 | 学习了如何求图图的广度和深度优先遍历,以及如何用Prim算法和Kruskal算法计算最小生成树等等。 |
-
计划学习时间:20小时
-
实际学习时间:22小时
-
改进情况:无





