Focal loss损失函数 所解决的问题

解决的问题：消除正负样本比例不平衡（One-Stage算法需要产生超大量的预选框，模型被大量负样本所主导，Focal Loss对此种情况卓有成效。），并且挖掘难负样本（难负样本即为一些很难区分是正样本还是负样本的负样本。其对立的就是一些简单的负样本，很容易区分出来是负样本，其前向传播的loss很小，模型很容易认出，因此在模型后期这些大量的简单样本会浪费大量的时间。）

Focal loss是在交叉熵损失函数基础上进行的修改，Focal loss损失函数降低了大量简单负样本在训练中所占的权重。首先回顾二分类交叉上损失：

 

其中 y 是真实样本的标签（1正0负）， y’ 是经过 sigmoid 激活函数的预测输出（数值在0-1之间）。可见普通的交叉熵对于正样本而言，输出概率越大损失越小。对于负样本而言，输出概率越小则损失越小。此时的损失函数在大量简单样本的迭代过程中比较缓慢且可能无法优化至最优。 

在此背景下，Focal Loss函数提出来了，

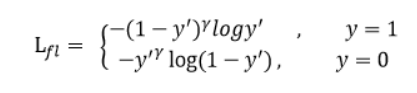
它在原有的基础之上加了一个γ，其中γ>0使得减少易分类样本的损失，使得模型更关注于困难的、错分的样本。

下图是γ的不同取值对损失函数曲线的影响

例如：

　　γ为2时，对于正类样本而言，预测结果为0.95肯定是简单样本，所以（1-0.95）的γ次方就会很小，这时损失函数值就变得比没有γ次方时更小，而预测概率为0.3的样本其损失相对很大，都加快了模型收敛的速度。

　　对于负类样本而言，预测0.1的结果应当远比预测0.7的样本损失值要小得多。对于预测概率为0.5时，损失值减少了0.25倍。所以更加关注于这种难以区分的样本。这样减少了简单样本的影响，大量预测概率很小的样本叠加起来后的效应才可能比较有效。

此外，加入平衡因子α，用来平衡正负样本本身的比例不均：论文中α取0.25，即正样本要比负样本占比小，这是因为负例易分。

 

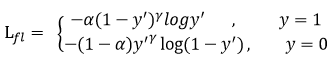
只添加α虽然可以平衡正负样本的重要性，但是无法解决简单与困难样本的问题。

γ调节简单样本权重降低的速率，当γ为0时即为交叉熵损失函数，当γ增加时，调整因子的影响也在增加。实验发现γ为2时最优。