机器学习——密度聚类

 

 

 

 

 

 简单来说：邻域就是范围，密度就是该范围内样本的个数。

　　　　　　核心点：设定一个阈值M，如果在该邻域内不包括某点本身，样本的个数大于阈值M,则此点就是核心点。

对于一个数据集来说，大部分都是核心点，因为邻域是我随便给的嘛，不是核心点的就是非核心点。

边界点：若此点不是核心点，但是此点的邻域内包含一个或多个核心点，那么此点为边界点

异常点：既不是核心点也不是边界点的就是异常点

直接密度可达：x1是核心点，x2,x3,x4,x5都在其邻域内，则皆直接密度可达

 

 密度可达：

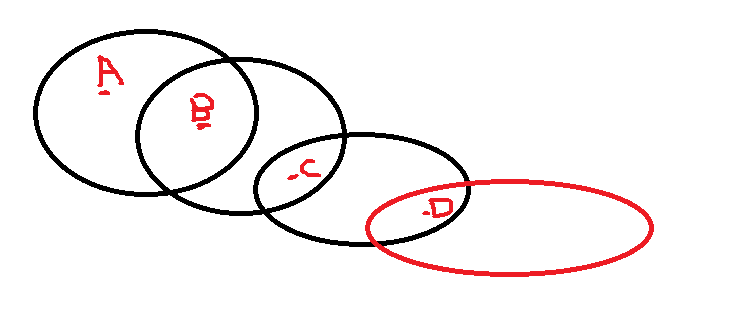
ABCD都是核心点，那么A到D密度可达

 

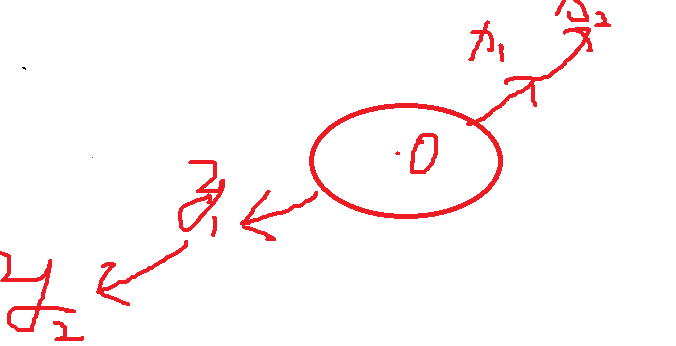
 密度相连：o到x2密度可达，o到y2密度可达，则Y2与x2密度相连

 

 

 

 

 

 

 

最大密度聚类算法（MDCA）：

步骤：①先找出最大密度点，即所有点的邻域内样本数最多的那个点

　　    ②计算其他所有点与最大密度点的距离，并从小到大排序

给定一个p值，p的意思是从小到大排序后的前几项

m值是阈值

　　  ③比如前2项吧。设第一项为x1，第二项为x2，如果x1与x2邻域内的样本数大于阈值m，那么x1与x2是核心点，其与最大密度点构成了一个簇，将最大密度点和x1,x2从原来的样本中删除，删除后的原样本再找一个最大密度点，继续此操作。

　　  ④如果x1邻域内的样本数大于m，但是x2邻域内的样本数小于m，那么暂时将其当做噪音点。再把x2和剩下的样本点找一个最大密度点，继续此操作

　　  ⑤最后得到一个个的小簇，再看簇间距离是否小于阈值m，若小于阈值m时，小簇要合并，直到不能合并为止。

注意：单个簇内，除去簇中心点，最大样本数为p

官方解释如下：