机器学习——聚类算法之K-means与K-means++,K-meansⅡ

相似度判定:
①距离,公式:
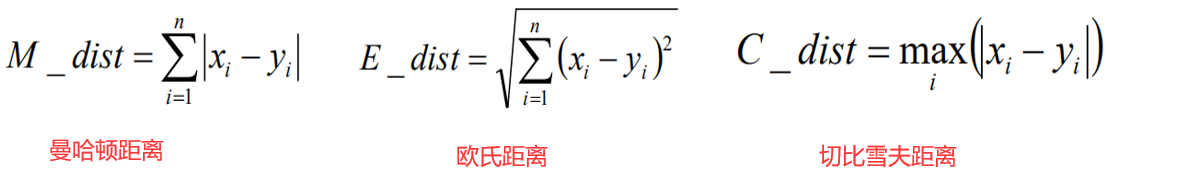
我们使用以欧式距离为主
②夹角余弦值:越大,相似度越高
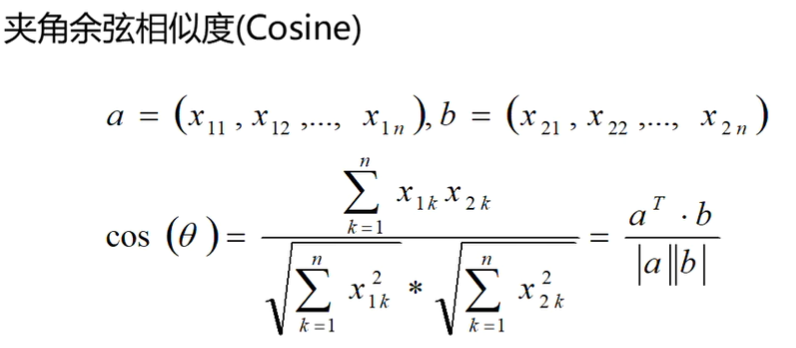
内积/模长
③杰卡德相似系数与相关系数

如上图,则说x1与x2相似,即为杰卡德相似系数,为保持和距离的性质一致性,所以1-杰卡德相似系数,相似系数也是一样
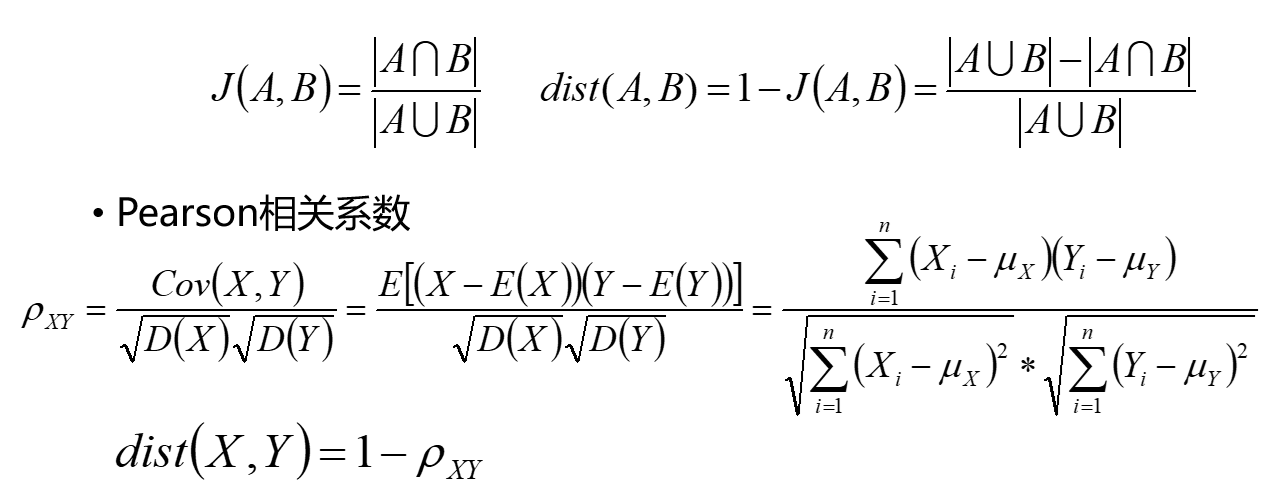
簇:聚类之后的类别,即为簇
聚类只有合理不合理,没有好与坏。
K-means:
从样本中随机抽取k个点作为初始簇中心点,计算一下其他样本到这几个点的距离,离哪个点近就归于哪一个类。
当所有样本点都以此分完后,簇中心点改为该簇里所有样本的均值。
然后以新的簇中心点再重新把所有样本分一次类。
一直如此循环,直到簇中心点不再变化或者变化极小为止。或者最小误差平方和(MSE,即该簇中所有样本点到簇中心点的距离之和)不再改变为止。
聚类效果影响因素:
①,k值的选取
②,初始簇中心点的选取,如果数据不均衡时,聚类效果就可能会不好
为什么取均值为簇中心点?原理:

存在异常点时

K-means算法需要解决的点:一开始随机选的那几个簇中心点如果挨得很近,可就完犊子了

优缺点:

K-means++算法:可以说是K-means的改进

为了解决K-means的缺点,有了
K-means Ⅱ算法:其实就是先小批量数据集做一次K-means聚类,再以此的结果作为初始簇中心点,为所有的数据做一次K-means.


