机器学习——GBDT算法与stacking算法
GBDT(梯度提升迭代决策树)
总结
优先解决回归问题,将第一个数据的残差传入到第二个数据中去
构建下一个数据集的数据是上一个数据集的残差
详述
GBDT也是Boosting算法的一种,但是和AdaBoost算法不同;区别如下:
AdaBoost算法是利用前一轮的弱学习器的误差来更新样本权重值,然后一轮一轮
的迭代;
GBDT也是迭代,但是GBDT要求弱学习器必须是回归CART模型,而且
GBDT在模型训练的时候,是要求模型预测的样本损失尽可能的小。优先做回归问题。
要求:把boosting算法的第一棵树,第二棵树...看成一种迭代,随着迭代加深,损失函数在逐渐减小,哪个方向上损失函数减小最快,负梯度方向。因此,构建下一个学习器时,传入的值就是负梯度值,仅此而已。也是残差
GBDT通过多轮迭代,每轮迭代产生一个弱分类器,每个分类器在上一轮分类器的残差基础上进行训练。对弱分类器的要求一般是足够简单,并且是低方差和高偏差的。因为训练的过程是通过降低偏差来不断提高最终分类器的精度。 方差越高,模型越复杂,越容易过拟合;偏差越高,模型越简单,越容易欠拟合。
备注:所有GBDT算法中,底层都是回归树。
原理如下图
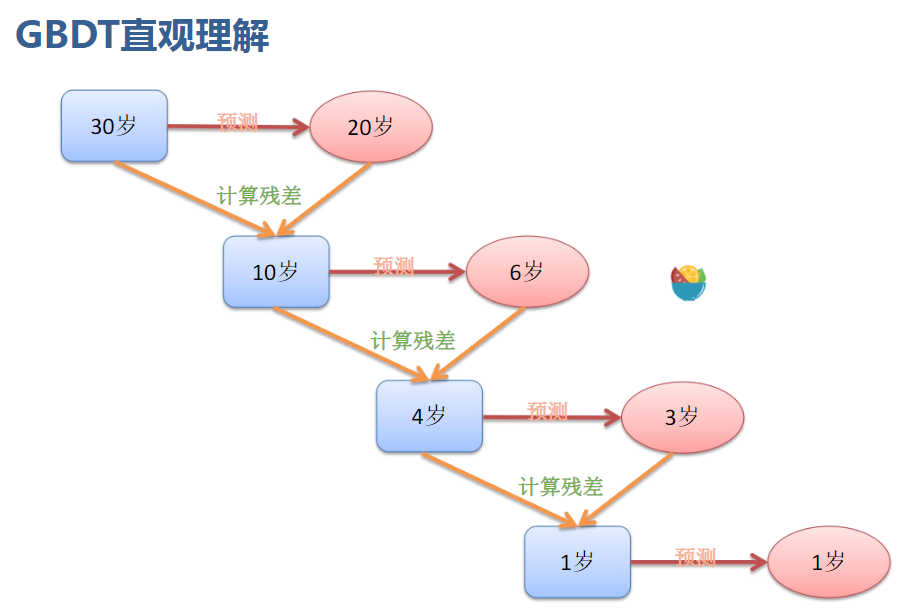
所有树的结果累加起来就是最终结果。
GBDT与随机森轮的区别:

F(X)是所有树加一起的回归值,我们要求的是下一棵树F*(X),argmin意思是F*(X)是多少的时候能达到损失函数最小,后面的F(X)是前M个回归器y的回归值之和。


我们要找的就是fm(Xi)是多少的时候,损失函数最小
以某一个叶子节点举例:

来个完整的例题!







Stacking
Stacking是指训练一个模型用于组合(combine)其它模型(基模型/基学习器)的技术。即首先训练出多个不同的模型,然后再以之前训练的各个模型的输出作为输入来新训练一个新的模型,从而得到一个最终的模型。一般情况下使用单层的Logistic回归作为组合模型。

