机器学习算法概述第五章——CART算法
特点:
是一个二叉树,元素可以重复利用,可以做回归也可以做分类,分类用最小二乘法,即误差平方和最小
切割方法:
对于可量化的x来说:
切割点通常为两个x的平均值
左右两部分分别取均值,再评判以哪个分割点的误差平方和最小,即第一层根节点为此点
以此为规则,往下迭代,构建出回归树
对于不可量化的x来说:
x无法去均值。直接以特征属性割分,再计算两个区域的均值,再寻找误差平方和最小的切割点
举个栗子:
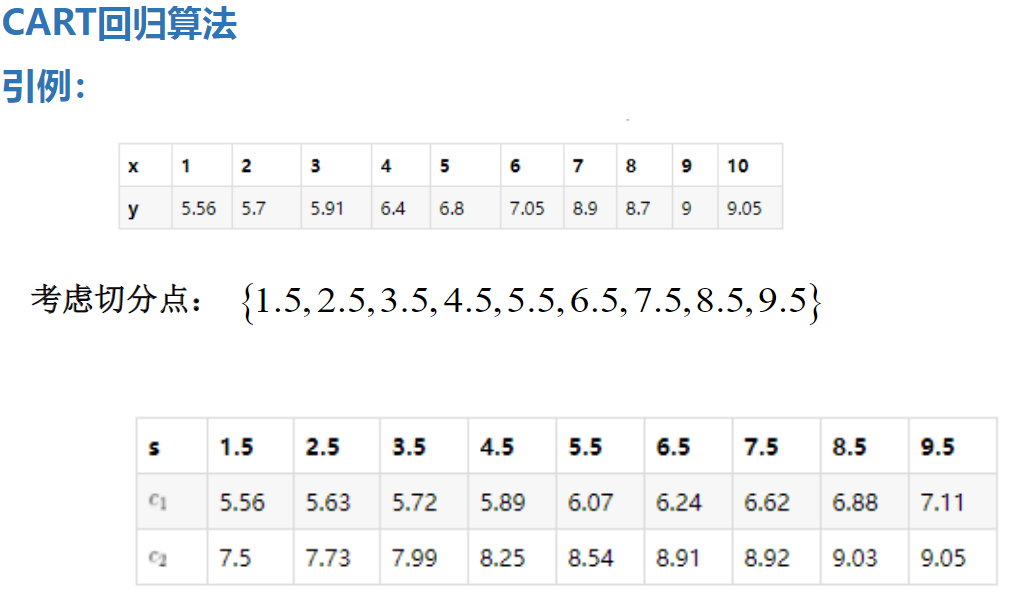
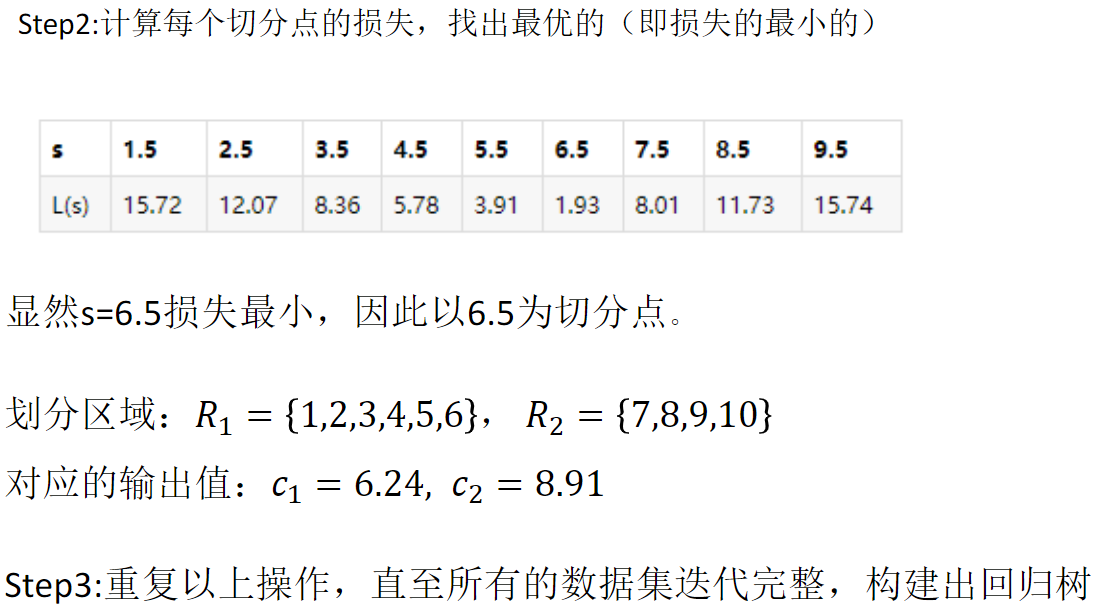
CART回归树的构建:


优点:
易于解释
处理类别特征,其他的技术往往要求数据属性的单一
延展到多分类
不需要特征放缩
能捕获非线性关系和特征间的交互关系
缺点:
寻找最优的决策树是一 个NP-hard的问题,只能通过启发式方法求次优解
决策树会因为样本发生- -点点的改动,就会导致树结构的剧烈改变
如果某些离散特征的特征值种类多,生成决策树容易偏向于这些特征ID3
有些比较复杂的关系,决策树很难学习,比如异或
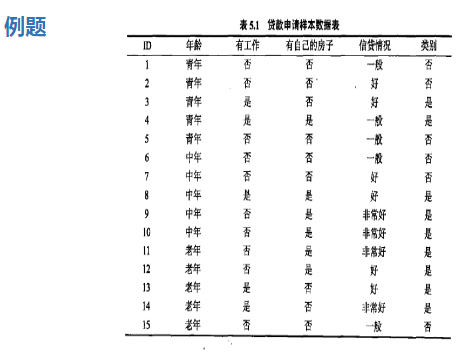
CART分类决策树算法:
纯度:当样本点均来自同一类别时不纯度为0,当两个样本点属于不同类别时的不纯度为两个类别的概率相乘
多类别时:
来自于1类别的概率+来自于2类别的概率+来自于3类别的概率
![]()
不纯度就是基尼系数,以基尼系数最小的一项为第一个切分点,基尼系数计算如下



cart分类树也是一个二叉树



总结
KD-tree目前接触到的是无监督的
ID3、C4.5和CART算法均只适合在小规模数据集上使用
ID3、 C4.5和CART算法都是单变量决策树
决策树分类- 般情况只适合小数据量的情况(数据可以放内存
CART算法是三种算法中最常用的一种决策树构建算法(sklearn中仅支持CART)。
三种算法的区别仅仅只是对于当前树的评价标准不同而已,ID3使用信息增益、
C4.5使用信息增益率、CART使用基尼系数。 (不是主要区别)
CART算法构建的一定是二 叉树,ID3和C4.5构建的不一 定是二 叉树。(主要区别)

C4.5在我们学习使用的sklearn上没有,所以我们是忽略掉了

