实验二:逻辑回归算法实验
| 20大数据三班 | 20大数据三班 |
| ---- | ---- | ---- |
|作业要求|作业要求|
| 学号 | 20161337 |
【实验目的】
理解逻辑回归算法原理,掌握逻辑回归算法框架;
理解逻辑回归的sigmoid函数;
理解逻辑回归的损失函数;
针对特定应用场景及数据,能应用逻辑回归算法解决实际分类问题。
【实验内容】
1.根据给定的数据集,编写python代码完成逻辑回归算法程序,实现如下功能:
建立一个逻辑回归模型来预测一个学生是否会被大学录取。假设您是大学部门的管理员,您想根据申请人的两次考试成绩来确定他们的入学机会。您有来自以前申请人的历史数据,可以用作逻辑回归的训练集。对于每个培训示例,都有申请人的两次考试成绩和录取决定。您的任务是建立一个分类模型,根据这两门考试的分数估计申请人被录取的概率。
算法步骤与要求:
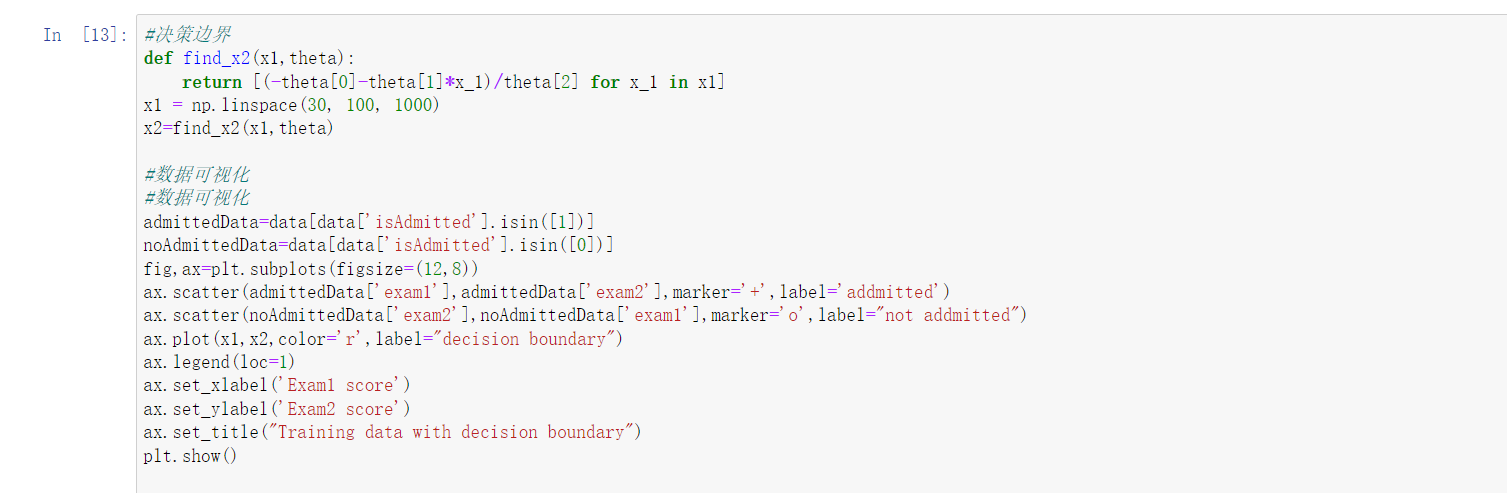
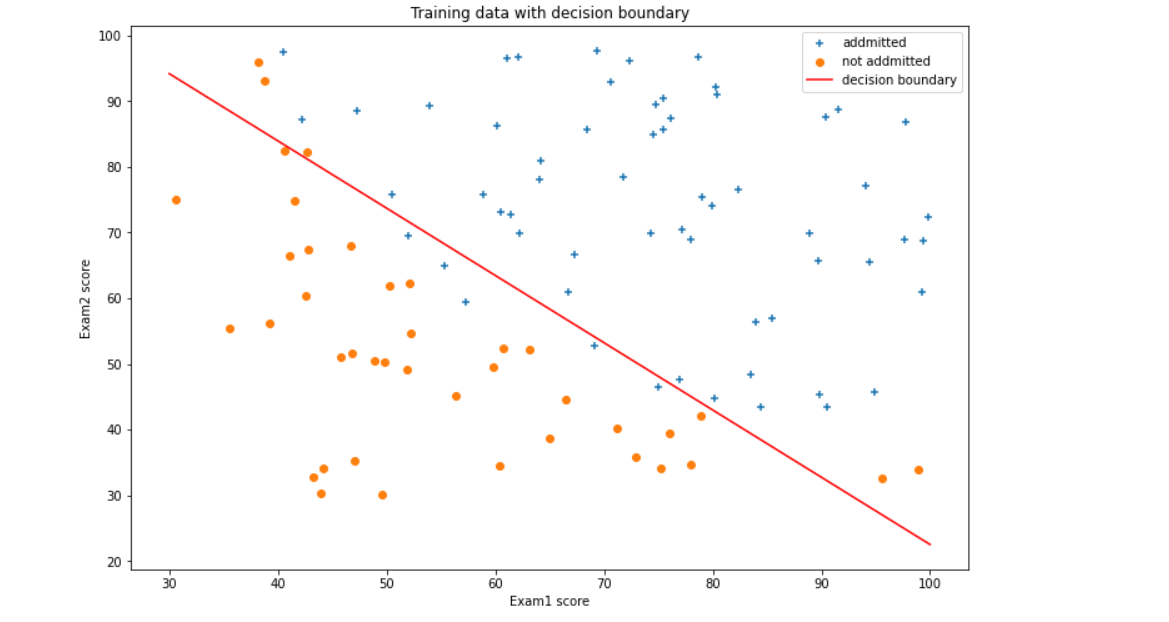
(1)读取数据;(2)绘制数据观察数据分布情况;(3)编写sigmoid函数代码;(4)编写逻辑回归代价函数代码;(5)编写梯度函数代码;(6)编写寻找最优化参数代码(可使用scipy.opt.fmin_tnc()函数);(7)编写模型评估(预测)代码,输出预测准确率;(8)寻找决策边界,画出决策边界直线图。
2. 针对iris数据集,应用sklearn库的逻辑回归算法进行类别预测。
要求:
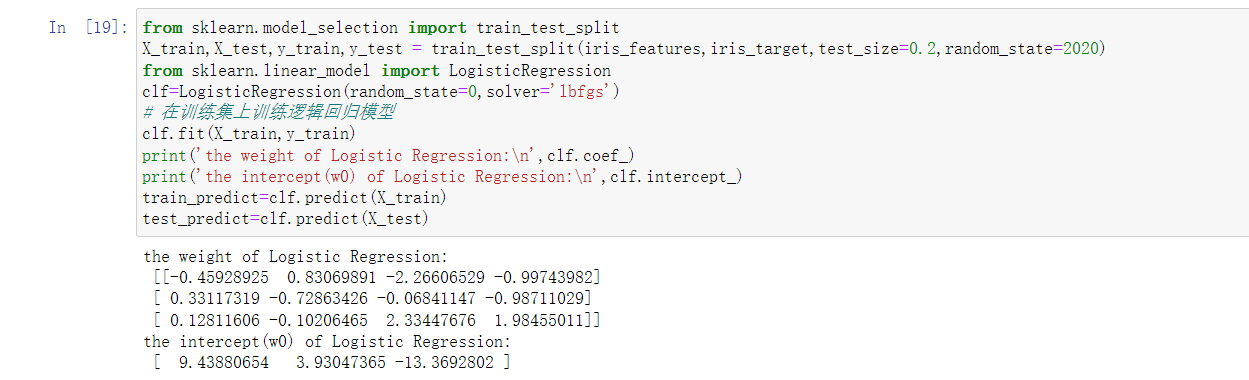
(1)使用seaborn库进行数据可视化;(2)将iri数据集分为训练集和测试集(两者比例为8:2)进行三分类训练和预测;(3)输出分类结果的混淆矩阵。
实验步骤:
引包

读取数据
绘制数据,看下数据分布情况


数据预处理

定义Sigmod函数
Sigmod函数
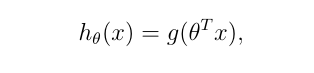
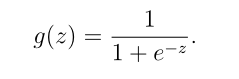

代价函数(Cost function)


梯度函数


寻找最优化参数(scipy.opt.fmin_tnc()函数)
在实现线性回归时,是利用梯度下降的方式来寻找最优参数。
在此处使用scipy.optimize包下的fmin_tnc函数来求解最优参数,该函数利用截断牛顿算法中的梯度信息,最小化具有受边界约束的变量的函数。
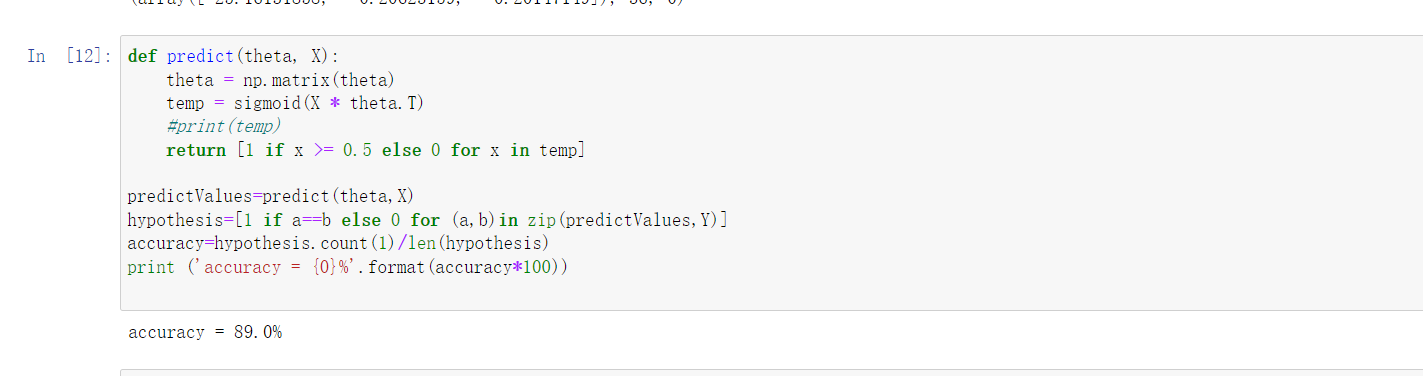
模型评估(准确率计算)
在求得最优theta值后,利用得到的模型在训练数据中进行预测,并求准确率。
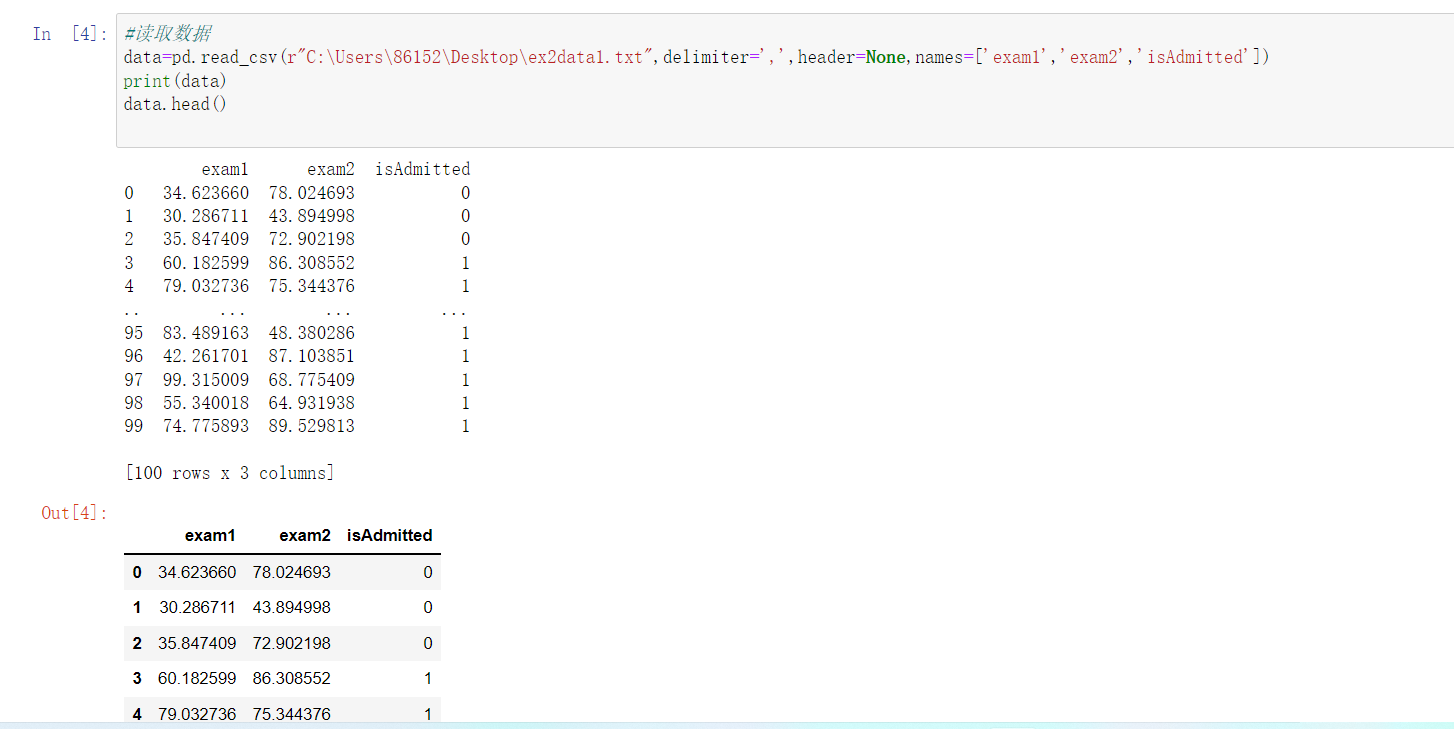
由逻辑回归的假设模型可知:
当hθ(x)>=0.5时,预测y=1;
当hθ(x)<0.5时,预测y=0;
predict函数:通过训练数据以及theta值进行预测,并且把预测结果使用列表返回;
hypothesis=[1 if a==b else 0 for (a,b)in zip(predictValues,Y)] 目的是将预测值与实际值进行比较,如果二者相等,则为1,否则为0;
accuracy=hypothesis.count(1)/len(hypothesis) 计算hypothesis中1的个数然后除以总的长度,得到准确率

预测准确率
决策边界
从Seaborn中导入鸢尾花数据集iris,该数据集时Pandas DataFrame数据类型

数据可视化(散点图,数据分布图)



将iri数据集分为训练集和测试集(两者比例为8:2)进行三分类训练和预测
输出分类结果的混淆矩阵。


相关公式:
Sigmod函数
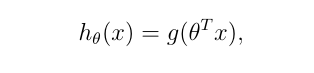
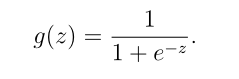
代价函数(Cost function)

梯度函数

逻辑回归算法的应用场景及存在的问题
应用场景:
用于分类场景, 尤其是因变量是二分类(0/1,True/False,Yes/No)时我们应该使用逻辑回归。
不要求自变量和因变量是线性关系
存在的问题:
防止过拟合和低拟合,应该让模型构建的变量是显著的。一个好的方法是使用逐步回归方法去进行逻辑回归。
逻辑回归需要大样本量,因为最大似然估计在低样本量的情况下不如最小二乘法有效。
独立的变量要求没有共线性。



