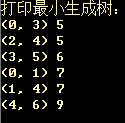
克鲁斯卡尔算法

环境： Codeblocks 13.12 + GCC 4.7.1

---

 

基本思想：（1）构造一个只含n个顶点，边集为空的子图。若将图中各个顶点看成一棵树的根节点，则它是一个含有n棵树的森林。（2）从网的边集 E 中选取一条权值最小的边，若该条边的两个顶点分属不同的树，则将其加入子图。也就是说，将这两个顶点分别所在的两棵树合成一棵树；反之，若该条边的两个顶点已落在同一棵树上，则不可取，而应该取下一条权值最小的边再试之（3）依次类推，直至森林中只有一棵树，也即子图中含有 n-1条边为止。

大白话：（1）将图中的所有边都去掉。（2）将边按权值从小到大的顺序添加到图中，保证添加的过程中不会形成环（3）重复上一步直到连接所有顶点，此时就生成了最小生成树。这是一种贪心策略。

---

 

难点：判断某条边<u, v>的加入是否会在已经选定的边集集合中形成环。

解决办法：使用并查集，分别找出两个顶点u, v所在树的根节点。若根节点相同，说明u, v在同一棵树中，则u, v连接起来会形成环；若根节点不同，则u, v不在一棵树中，连接起来不会形成环，而是将两棵树合并。

---

 

 

图解过程：原图如下                                               边集数组按权值顺序排列

           

                

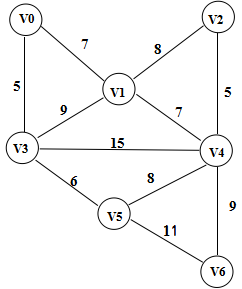
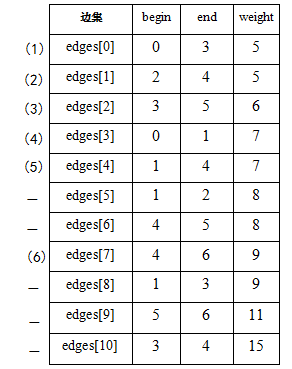
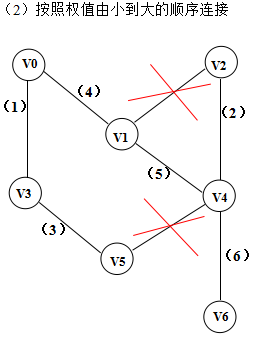
边<1, 2>和<4, 5>在添加到图中的时候形成了环，所以不能将v1和v2，v4和v5连起来。

---

 

判断是否成环

int Find(int *parent, int f) {
    while ( parent[f] > 0) {
        f = parent[f];
    }
    return f;
}

    for (i = 0; i < G.numEdges; i++) {
        n = Find(parent, edges[i].begin);//寻找边edge[i]的“首节点”所在树的树根
        m = Find(parent, edges[i].end);//寻找边edge[i]的“尾节点”所在树的树根

        //假如n与m不等，说明两个顶点不在一棵树内，因此这条边的加入不会使已经选择的边集产生回路
        if (n != m) {
            parent[n] = m;
            printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
        }
    }

代码：

//克鲁斯卡尔算法
//在连通网中求出最小生成树

#include <stdio.h>
#include <stdlib.h>

#define MAXEDGE 20
#define MAXVEX  20
#define INFINITY 65535

typedef struct
{
    int arc[MAXVEX][MAXVEX];
    int numVertexes, numEdges;//顶点数，边数
}MGraph;

typedef struct
{
    int begin;
    int end;
    int weight;
}Edge;   //对边集数组Edge结构的定义

//创建图的邻接矩阵
void CreateMGraph(MGraph *G) {
    int i, j;

    G->numEdges=11;
    G->numVertexes=7;

    for (i = 0; i < G->numVertexes; i++) {
        for ( j = 0; j < G->numVertexes; j++) {
            if (i==j)
                G->arc[i][j]=0;
            else
                G->arc[i][j] = G->arc[j][i] = INFINITY;
        }
    }
    G->arc[0][1]=7;
    G->arc[0][3]=5;
    G->arc[1][2]=8;
    G->arc[1][3]=9;
    G->arc[1][4]=7;
    G->arc[2][4]=5;
    G->arc[3][4]=15;
    G->arc[3][5]=6;
    G->arc[4][5]=8;
    G->arc[4][6]=9;
    G->arc[5][6]=11;

    for(i = 0; i < G->numVertexes; i++) {
        for(j = i; j < G->numVertexes; j++) {
            G->arc[j][i] =G->arc[i][j];
        }
    }

}

//快速排序的条件
int cmp(const void* a, const void* b) {
    return (*(Edge*)a).weight - (*(Edge*)b).weight;
}

//找到根节点
int Find(int *parent, int f) {
    while ( parent[f] > 0) {
        f = parent[f];
    }
    return f;
}

// 生成最小生成树
void MiniSpanTree_Kruskal(MGraph G) {
    int i, j, n, m;
    int k = 0;
    int parent[MAXVEX]; //用于寻找根节点的数组

    Edge edges[MAXEDGE]; //定义边集数组,edge的结构为begin,end,weight,均为整型

    // 用来构建边集数组并排序(将邻接矩阵的对角线右边的部分存入边集数组中)
    for ( i = 0; i < G.numVertexes-1; i++) {
        for (j = i + 1; j < G.numVertexes; j++) {
            if (G.arc[i][j] < INFINITY) {
                edges[k].begin = i; //编号较小的结点为首
                edges[k].end = j;   //编号较大的结点为尾
                edges[k].weight = G.arc[i][j];
                k++;
            }
        }
    }

    //为边集数组Edge排序
    qsort(edges, G.numEdges, sizeof(Edge), cmp);

    for (i = 0; i < G.numVertexes; i++)
        parent[i] = 0;

    printf("打印最小生成树：\n");
    for (i = 0; i < G.numEdges; i++) {
        n = Find(parent, edges[i].begin);//寻找边edge[i]的“首节点”所在树的树根
        m = Find(parent, edges[i].end);//寻找边edge[i]的“尾节点”所在树的树根

        //假如n与m不等，说明两个顶点不在一棵树内，因此这条边的加入不会使已经选择的边集产生回路
        if (n != m) {
            parent[n] = m;
            printf("(%d, %d) %d\n", edges[i].begin, edges[i].end, edges[i].weight);
        }
    }
}

int main(void)
{
    MGraph G;
    CreateMGraph(&G);
    MiniSpanTree_Kruskal(G);

    return 0;
}