数字逻辑综合 DC 相关理解 （二）

1. 线负载模型

  • 根据模型中提供的扇出-线网长度对应表，可以根据线网扇出负载估计线网长度。
    • 根据线网长度和阻抗、容抗、面积对应表格计算线上参数和延时信息。
  • 根据延时计算方式，电容和电阻有不同的组合方式，主要有三种模型：
    • worst_case_tree
    • best_case_tree
    • balanced_tree
  • 指令如下，-name为指定线负载模型名字，来源于工艺库，-library指定工艺库。
    set_wire_load_model -name $WIRE_LOAD_MODEL -library $LIB_NAME
  • 按照模块内部子系统net所采用模型分类
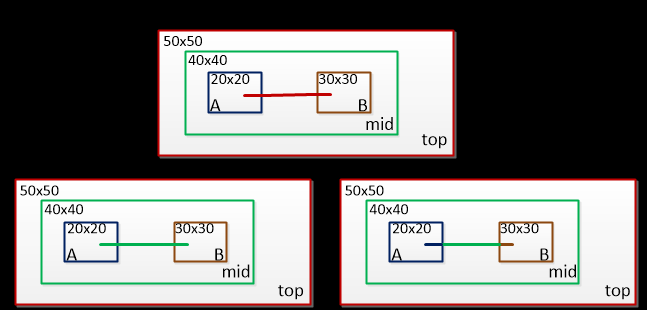
    • TOP
      • 该模式下，内部所有的子模块或者子系统都将会使用TOP层所设置的线负载模型，因此会覆盖所有的子模块的设置值。
      • 由于top层电路规模最大，如果子模块也使用其线负载模型计算，那么最悲观。
    • ENCLOSED
      • 该模式下，会默认选择能够cover整个net路径层次的线负载模型，并不一定是TOP层；
      • 相较于TOP模式下，延时要短一些。
    • SEGMENTED
      • 该模式下，则严格根据所设置对象的范围分别使用对应的线负载模型；
    set_wire_load_mode enclosed
  • 也可以使用默认的线负载模型，指令如下；DC工具在默认情况下会根据设计的cell面积自动选择合适的线负载模型。
set auto_wire_load_selection true
  • 线负载模型的设置在综合阶段可以初步的衡量net的延迟，但是在Routing之后，可以使用寄生参数提取工具，如STARRC抽取的SPEF文件，往往用于STA，根据其寄生参数计算net delay，此时的值会更加具备参考性。

2. 时钟属性

  • 时钟不确定性（uncertainty）包括skew和jitter。
  • 对于建立时间，考虑的时钟不确定需要包括受前级和本级skew值的影响、本级jitter值以及建立时间裕量。
    • 由于是建立时间，需要考虑前级寄存器时钟skew往后移Aps，本级寄存器时钟往前移Bps，那么skew所导致的不确定时间为(A+B)ps。

2.1 时钟偏移（skew）

  • 由于线网等延时，导致时钟信号到达寄存器口存在相位差。
  • 其与时钟频率没有直接关系，与时钟线的长度及时钟线驱动的时序单元负载电容、个数有关。
  • skew 可以分为四类。
    • Interclock skew
      • 不同时钟域之间两条路径的最大skew。
    • Global skew
      • 同一个时钟域下，任意两条路径的最大skew。
    • Local skew
      • 同一个时钟域下，任意两条有时序关系的路径的最大skew。
    • Useful skew
      • 可以在ICC，设置指令skew_opt。向前或者向后 slack较为充裕的路径借时间来修正violation。具体指令使用可见ICC userguide 5-159页。
  • 更多关于skew对建立、保持时间影响的可以看这篇博客。
    • 总结来说，Positive skew，setup检查宽松，hold检查更严格。Negative skew，setup检查严格，hold检查更宽松。
      • Postive和Negative的划分是根据时钟分支点到launch寄存器和capture寄存器skew大小的比较；前者<后者，则为Positive；后者<前者，则为Negative。

2.2 时钟抖动（jitter）

  • 不随时间积累，时而超前、时而滞后的偏移。与时钟频率也无直接关系。
  • 包括随机抖动和固定抖动
    • 随机抖动来源于：热噪声、Flicker Noise等，与电子器件和半导体器件的电子和空穴特性有关。选择合适的工艺可以得到更小的随机抖动。
    • 固定抖动来源于：开关电源噪声、串扰、电磁干扰等。可以通过优化设计改善固定抖动；如选择合适的电源滤波方案、合理的PCB布局布线。

2.3 时钟延迟（latency）

  • 时钟信号从时钟源（例如：晶振）触发到达触发器时钟端口的延时，为时钟延迟。
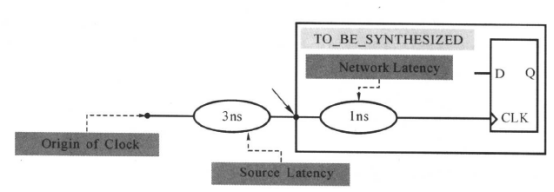
    • 主要包括时钟源延迟（source latency）和 时钟网络延迟（network latency）。

2.4 CTS之前 模拟时钟树的建模

  • （1）clk transition，模拟时钟树的驱动能力和负载。
  • （2）clk uncertainty，主要是模拟skew。
  • （3）clk latency，模拟时钟树线网延时。

3. 时序约束实例

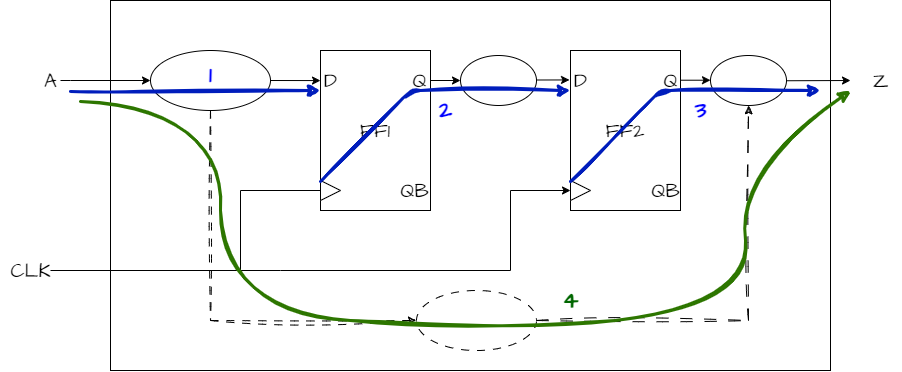
3.1 路径2的约束

  • 为了满足FF2的建立时间要求，触发器翻转时间 $ T_{clk2q}$ +寄存器和寄存器之前的组合逻辑延时 $ T_{logic}+t_{setup-FF2}$ ＜ 时钟周期。
  • 保持时间一般是满足的，因为传输的延时(\(T_{clk2q}+T_{logic}\))一般都会大于触发器的保持时间。

3.2 路径1的约束

img

  • 首先需要告诉DC被综合模块外的延时为 \(T_{clk2q}+T_M\)，留下的时间为 \(T_{clk}-T_{clk2q}-T_M\)，将其与 \(T_n+T_{setup}\) 时间相比较，如果 \(T_n\) 太大，那么DC会对其进行优化，如果最优解也大于留下的时间，那么就会报错。
    • 假设我们已知输入端口外部电路的延迟为4ns，那么可以使用DC的约束指令
    set_input_delay  -max 4 -clock  CLK  [get_ports   A]
set_input_delay 3.5 -max -clock clk1 [remove_from_collection [all_inputs][get_ports clk1]]
# 命令表示从所有的输入端口中除掉时钟clk
  • 前面介绍的是不考虑不确定因素的情况，当考虑时钟不确定性，有以下分析
    • 假设时钟不确定时间为U，假设触发器的建立时间为1ns，外部输入延时为D，那么内部N逻辑所允许的最大延迟S为：
      • \(S = T_{clk}-D-U-1\)

3.3 路径3的约束

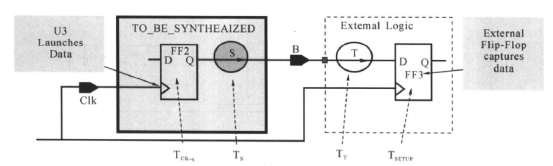
  • 告诉DC要综合的模块外部电路延时为 \(T_t+T_{FF3setup}\) 留下的时间为 \(T_{clk}-T_t-T_{FF3setup}\) 时间，将这个值与\(T_{clk2q}+T_s\) 相比较，如果 $ T_s$ 太大，那么DC会对其进行优化，如果最优解也大于留下的时间，那么就会报错。
    • 假设DC约束指令如下
    create_clock  -period 20  [get_ports Clk]
set_output_delay  -max  7.0  -clock   Clk  [get_ports  B]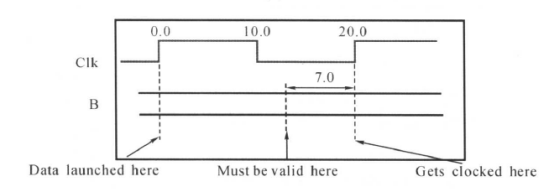
  • 上面是没有考虑时钟不确定的，假设综合模块内部延时为S（包含 \(T_{clk2q}\) 和组合逻辑延时），外部输出延时为X（包括外部组合逻辑和后级寄存器的建立时间），时间不确定度为Y，时钟周期为T。
    • 满足 \(T-S-Y=X\)。

3.4 路径4的约束

  • 分为两种情况
    • 模块内部除了从输入到输出的组合逻辑外还有时序逻辑。
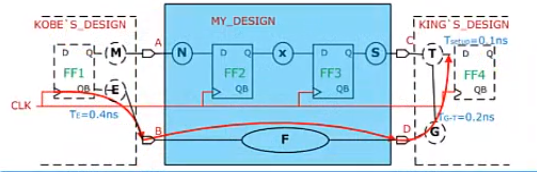
      set_input_delay  0.4  -clock  CLK  -add_delay [get_ports B]
set_output_delay    0.2  -clock  CLK  -add_delay [get_ports D]
set_max_delay   $CLK_PERIOD  -from [get_ports B]  -to  [get_ports D]
      • DC计算 $ T>E+F+U+G $（其中U为不确定时间）。
    • 模块内部都是组合逻辑，没有时序逻辑，这种需要使用虚拟时钟的概念。
posted @ 2023-06-26 15:58  可达达鸭  阅读(218)  评论(0)  编辑  收藏  举报