Python:n个点的费马问题
问题描述
在平面内有n(n>=3)个点N1(x1,y1),N2(x2,y2),...,Nn(xn,yn),现求一点P(x,y),使得P到各点直线距离之和最小。
算法分析
当n=3时,这是著名的三角形费马点问题,网上有详细介绍和证明。
然而,那些平面几何证明看似巧妙,但真正涉及到了n个点的时候,就只能呵呵了,还是得用解析法来想办法。
目标函数为:
![]()
我们需要求它的最小值。
分别对x和y求偏导数:
fx(x,y) =![]() =0
=0
fy(x,y) =![]() =0
=0
当两偏导数同为0的时候,是此二元函数的驻点。
这里,若再求一次偏导数(二阶偏导数):
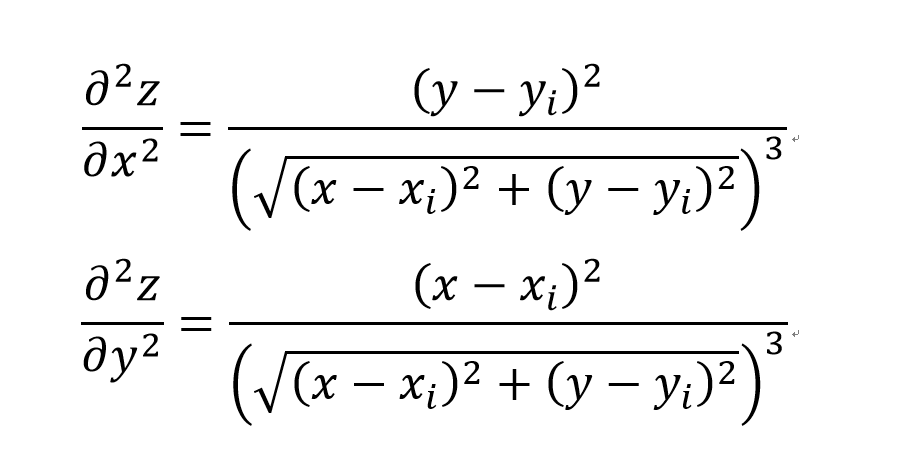
发现其恒大于0,即原函数是个凸函数,一阶偏导数为0的点就是它的最小值点。
那么上面这俩方程(一阶偏导数为0)怎么解呢?
这里就要隆重推出:迭代法。
说句题外话,我们用通俗的说法来辨析几个词:循环、迭代、递归、遍历。我们常常把它们混用,但它们其实是互不相同的!
循环Repeating:反复执行一段程序代码。例如:while循环、for循环...
迭代Iteration:每一次的运算结果会成为下一次运算的初始值,经常用此方法以不断逼近目标结果。例如:牛顿迭代法、二分法、斐波那契数列...
递归Recursion:(函数等)自己调用自己。例如:汉诺塔问题、斐波那契数列...
遍历Traversal:访问一个树的所有结点,每个只访问一次。例如:广度优先搜索、深度优先搜索...
可以看出,有些问题可能会同时涉及到这四个中的多个(其实也不难理解),这大概就是我们常常混淆这四个词的一大原因吧。比如,实现后三者的程序,写代码时基本都跑不掉循环结构,很多人从此就开始混淆它们了...而其实,很多时候它们的思想也是相通的,因此造成了一个问题既可以用迭代也可以用递归的现象,这很正常。
回到本文的问题。我们尝试解一个方程f(x)=0,如果能找到一个g(x)=f(x)+x,从而将原方程转化为x=g(x).通过不断迭代:g(g(g(g(g(x))))),逼近解x。
这其实就是高中数学(一般在竞赛中出现,或是十多年前的很难的高考数学的数列题里出现)里的“不动点”问题。
一个经典的例子就是利用cos(cos(cos(0)))解方程cos(x)=x。利用作图能清晰的看出:

当然了,此种方法对g(x)的图形和x的初始值是有要求的,不然有可能不但不逼近,反而跑的越来越远了。
例如,对于方程3^x-7=x,我们直观的感觉它有两个解,运行如下代码,轻松得到了一个解-6.9995。
import math
m=0
for i in range(10):
m=3**m-7
print(m)
可另外一个解呢?此种方法就很难求了,因为一旦迭代就离它越来越远了。我们尝试更改初始值如m=7来求那个正数的解:
根本执行不了。其实在草稿纸上画画图就能发现,想得到那个解,通过我们这种方法根本不能收敛。
不扯远了,再次回到本题,将x和y可以表示为:
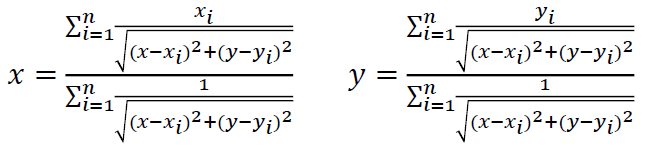
初始值可设为那n个点的重心,其实,最终答案一般都不会离重心太远。
至于为什么本题就可以收敛?由二阶导数>0恒成立知,一阶导数单调,故上述方程仅有一个根。
我们可以作图看看右边这个奇怪的函数和函数f(x)=x的交点,运行以下代码:
import math
import random
import matplotlib.pyplot as plt
a1=[];a2=[]
for i in range(6):
a1.append(random.random())
a2.append(random.random())
for j in range(1000):
x=j/1000;y=j/1000
xfenzi=0;xfenmu=0;yfenzi=0;yfenmu=0
for i in range(6):
g=math.sqrt((x-a1[i])**2+(y-a2[i])**2)
xfenzi=xfenzi+a1[i]/g
xfenmu=xfenmu+1/g
yfenzi=yfenzi+a2[i]/g
yfenmu=yfenmu+1/g
xn=xfenzi/xfenmu
yn=yfenzi/yfenmu
plt.scatter(x,xn,color='b',s=1)
plt.scatter(x,x,color='g',s=1)
plt.show()
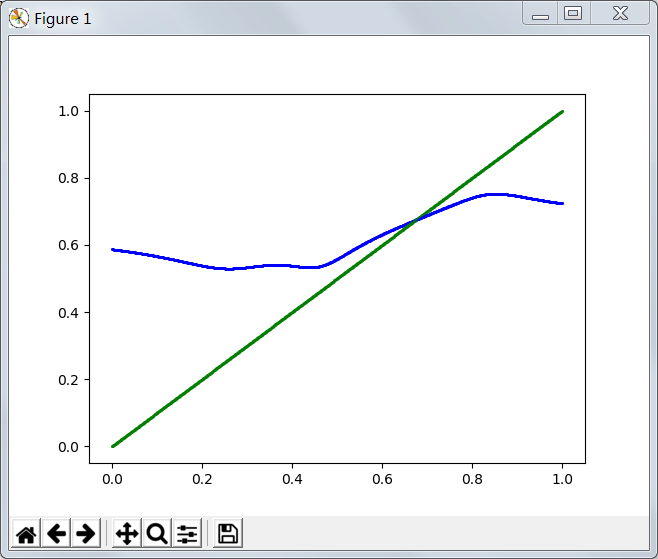
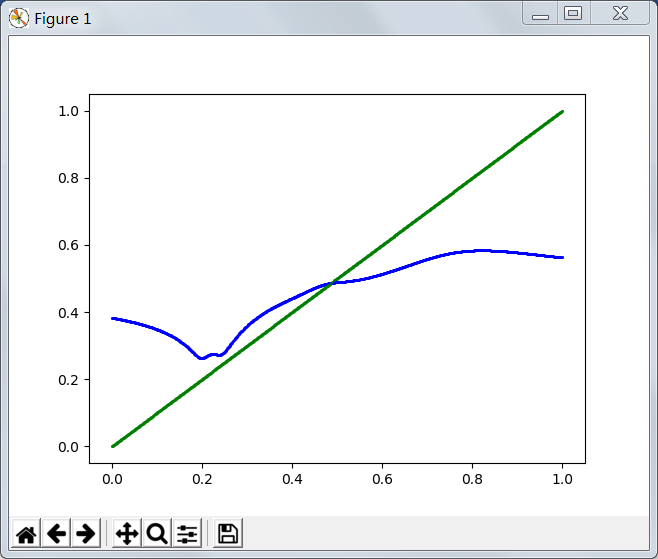
由上述,显然,不论怎么运行,仍是只有一个根。而且很明显这个图形是符合我们描述的那个迭代的,即:通过迭代能逐渐逼近那个交点。
因此,我们可以用迭代法实现找出平面上到n个点距离之和的最小值的费马点了。
以下是Python实现代码:
import math
import random
import matplotlib.pyplot as plt
n=int(input('请输入n:'))
a1=[];a2=[]
for i in range(n):
a1.append(random.random())
a2.append(random.random())
plt.scatter(a1,a2,color='r')
x=sum(a1)/n;y=sum(a2)/n
while True:
xfenzi=0;xfenmu=0;yfenzi=0;yfenmu=0
for i in range(n):
g=math.sqrt((x-a1[i])**2+(y-a2[i])**2)
xfenzi=xfenzi+a1[i]/g
xfenmu=xfenmu+1/g
yfenzi=yfenzi+a2[i]/g
yfenmu=yfenmu+1/g
xn=xfenzi/xfenmu
yn=yfenzi/yfenmu
if abs(xn-x)<0.01 and abs(yn-y)<0.01:
break
else:
x=xn
y=yn
plt.scatter(x,y,color='b')
plt.show()
运行效果:
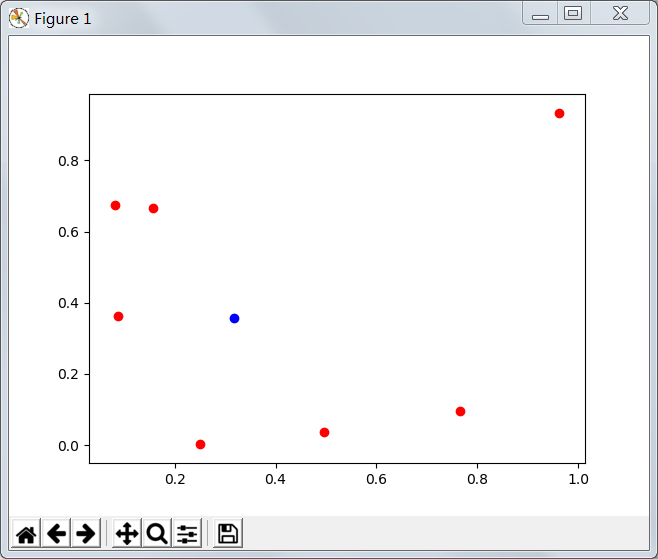
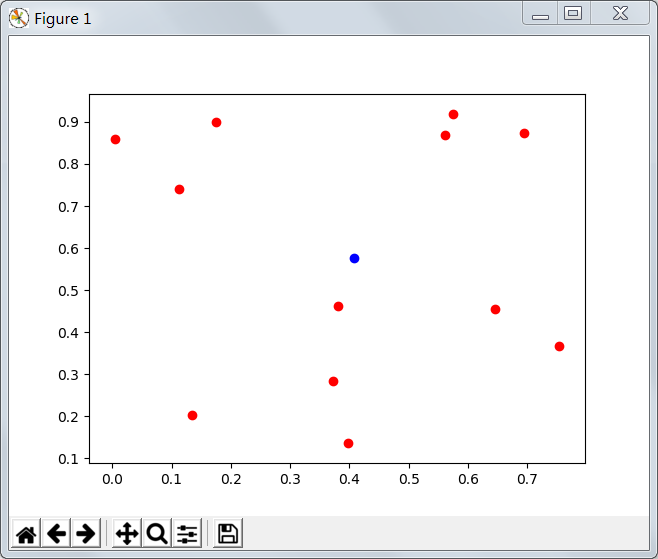

 浙公网安备 33010602011771号
浙公网安备 33010602011771号