机器学习第一次作业

第一章：机器学习概述

人工智能主要包括感知智能（比如图像识别、语言识别和手势识别等）和认知智能（主要是语言理解知识和推理）。它的核心是数据驱动来提升生产力、提升生产效率。
机器学习相关技术属于人工智能的一个分支。其理论主要分为如下三个方面：

传统的机器学习：包括线性回归、逻辑回归、决策树、SVM、贝叶斯模型、神经网络等等。

深度学习（Deep Learning）：基于对数据进行表征学习的算法。好处是用非监督式或半监督式的特征学习和分层特征提取高效算法来替代手工获取特征。

强化学习（Reinforcement Learning）：强调如何基于环境而行动，以取得最大化的预期利益。其灵感来源于心理学中的行为主义理论，即有机体如何在环境给予的奖励或惩罚的刺激下，逐步形成对刺激的预期，产生能获得最大利益的习惯性行为。和标准的监督式学习之间的区别在于，它并不需要出现正确的输入/输出对，也不需要精确校正次优化的行为。强化学习更加专注于在线规划，需要在探索（在未知的领域）和遵从（现有知识）之间找到平衡。

模式识别基本概念

定义

1.根据已有知识的表达，针对待识别模式，判别决策其所属的类别或者预测其对应的回归值。
2.模式识别本质上是一种推理过程。
3.根据任务，模式识别可以划分为“分类”和“回归”两种形式。分类的输出量是离散的类别表达，回归的输出量是连续的信号表达（回归值）。回归是分类的基础。

数学解释

模式识别可以看作一种函数映射f(x)将待识别模式x从输入空间映射到输出空间，函数f(x)是关于已有知识的表达。其输出可以是确定值也可以是概率值。

模型

1.模型是关于已有知识的一种表达方式，即函数f(x)。
2.特征提取：从原始输入数据提取更有效的信息。
3.回归器：将特征映射到回归值。
4.判别函数使用一些特定的非线性函数来实现，记作函数g。二类分类的时候使用的判别器是sign函数，多类分类的时候使用的判别器是max函数。

特征的概念

1.可以用于区分不同类别模式的、可测量的量
2.具有辨别能力：提升不同类别之间的识别性能
3.鲁棒性：针对不同的观测条件，仍能够有效表达类别之间的差异性
4.特征向量：指多个特征构成的（列）向量，长度为向量的模，方向为特征向量除其模长
5.特征空间：每个坐标轴表示一个特征，空间中和坐标原点相连的向量代表着该模式的特征向量

机器学习的分类

监督式学习

1.训练样本及其输出真值都给定情况下的机器学习，是最常见的学习方式
2.监督式学习问题可以进一步被分为回归和分类问题
3.通常使用最小化训练误差作为目标函数进行优化

无监督式学习

1.只给定训练样本、没有给输出真值情况下的机器学习算法，难度远高于监督式学习
2.无监督式学习的目标是对数据中潜在的结构和分布建模，以便对数据作更进一步的学习。
3.通常根据训练样本之间的相似程度来进行决策，典型应用有聚类和图像分割

半监督式学习

1.既有标注的训练样本、又有未标注的训练样本情况下的学习算法
2.半监督式学习问题介于监督式和非监督式学习之间。
许多现实中的机器学习问题都可以归纳为这一类。因为对数据加上标注耗时耗力，对于非专业人士也有一定的阻碍。而无标注数据的收集存储都是极为方便的
3.可以看作有约束条件的无监督式学习问题，即标注过的训练样本用作约束条件，典型应用有网络流数据

强化学习

1.真值滞后反馈的过程，适用于累积多次决策动作才能知道最终结果好坏，很难针对单次决策给出对应的真值的任务，例如棋类游戏。

模型的泛化能力

1.泛化能力指,机器学习方法训练出来一个模型,对于已知的数据(训练集)性能表现良好,对于未知的数据(测试集)也应该表现良好的机器能力
2.泛化能力低的表现
过拟合：在训练阶段表现良好在测试阶段表现很差
提高泛化能力：不要过度训练
模型选择
引入正则项
3.多项式拟合超参数

评估方法与性能指标

留出法

留出法直接将数据集D DD划分为两个互斥的部分，其中一部分作为训练集S SS，另一部分用作测试集T TT。

第二章：基于距离的分类器

MED分类器

1.基于距离的决策：把测试样本到每个类之间的距离作为决策模型，将测试样本判定为与其距离最近的类。
2.判别公式𝑦∈𝐶1,𝑖𝑓𝑑(𝑦,𝐶1)<𝑑(𝑦,𝐶2)
3.med分类器的问题：MED分类器采用欧氏距离作为距离度量，没有考虑特征变化的不同及特征之间的相关性。
4.类的原型：

均值：该类中所有训练样本的均值作为类的原型
最近邻：从一类的训练样本中，选取与测试样本距离最近的一个训练样本，作为该类的原型。类的原型取决于测试样本。

5.距离度量的标准：同一性、非负性、对称性、三角不等式。
6.常见的几种距离度量：欧式距离、曼哈顿距离、加权欧式距离

特征白化

1.目的：将原始特征映射到一个新的特征空间，使得在新空间中特征的协方差矩阵为单位矩阵，从而去除特征变化的不同及特征之间的相关性。
-特征正交白化：将特征转换分为两步：先去除特征之间的相关性（解耦, Decoupling），
然后再对特征进行尺度变换（白化, Whitening），使每维特征的方差相等。
2.令𝑊=𝑊2𝑊1

解耦：通过𝑊1实现协方差矩阵对角化，去除特征之间的相关性。
白化：通过𝑊2对上一步变换后的特征在进行尺度变换，实现所有特征具有相同方差。
𝑊1：1.求解协方差矩阵的特征值和特征向量。2.由特征向量构建转换矩阵𝑊1

3.如果矩阵不是方阵，则需要做奇异值分解。
4.𝑊1只是起到旋转的作用，转换前后欧式距离保持一致。新的特征的协方差是对角阵，对角线上的元素由原协方差矩阵的特征值构成。
5.特征白化后的欧式距离变为了马氏距离。𝑑2𝐸(𝑦1.𝑦2)=(𝑥1−𝑥2)𝑇∑−1𝑥(𝑥1−𝑥2)

MICD分类器

概念

二分类时当Σ1、Σ2是任意值时，MICD的决策边界是一个超抛物面或者超双曲面

MICD分类器的缺陷是会选择方差较大的类。

半个课程下来，目前还停留在理论阶段，概率论倒是还记得，高数和线代半斤八两，机器学习是门实践和理论结合密切的学科，网上查阅资料文献的时候，看到

对于此前不是机器学习/深度学习这个领域的朋友，不管此前在其他领域有多深的积累，还请以一个敬畏之心来对待。
持续的投入：三天打鱼两天晒网的故事，我们从小便知，不多说了；
系统的学习：一个学科，知识是一个体系，系统的学习才可以避免死角，或者黑洞；
大量的练习：毕竟机器学习/深度学习属于Engineering & Science的范畴，是用来解决实际的问题的。单纯的理论研究，如果没有实际的项目（包括研究项目）经验做支撑，理论可能不会有很大突破。

第三章贝叶斯决策与学习

贝叶斯决策与Map分类器

后验概率

贝叶斯规则

Map分类器

Map分类器：高斯观测概率

观测概率：单维高斯分布

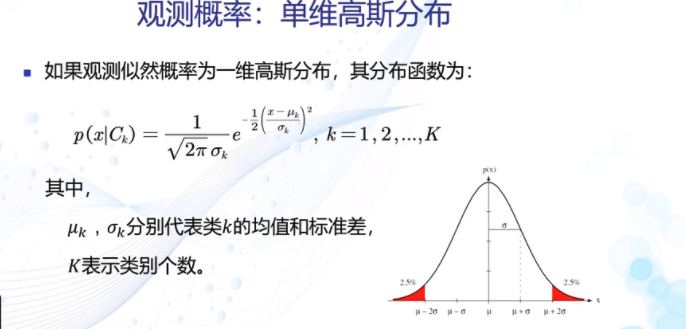
观测概率：高维高斯分布

决策风险与贝叶斯分类器

决策风险的评估

贝叶斯分类器

最大似然估计

监督式学习方法：

参数化方法：给定概率分布的解析表达，学习这些解析表达函数中的参数。该类方法也称为参数估计。常用的有最大似然估计、贝叶斯估计。
非参数化方法：概率密度函数形式未知，基于概率密度估计技术，估计非参数化的概率密度表达。

目标函数：给定所有类的𝑁个训练样本，假设随机抽取其中一个样本属于𝐶1类的概率为𝑃，则选取到𝑁1个属于𝐶1类样本的概率为先验概率的似然函数（即目标函数）

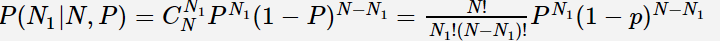
先验概率估计