01背包详解

\(01背包详解\) 顺带几题完全背包问题

\(update:\)

2019.4.4 初稿。
2019.4.13 重改加上一些注释 顺便加几道完全背包题目。以及调整Markdown。

本文涉及到的题目
\(\small \ P1048\ 采药\)
\(\small \ P1049\ 装箱问题\)
\(\small \ P1060\ 开心的金明\)
\(\small \ P1164\ 小A点菜\)
\(\small \ P2639\ [USACO09OCT]Bessie的体重问题\ Bessie's We…\)
\(\small \ P1794\ 装备运输_NOI导刊2010提高\ （04）\)
\(\small \ P1877\ [HAOI2012]音量调节\)
\(\small \ P1910\ L国的战斗之间谍\)
\(\small \ P2871\ [USACO07DEC]手链Charm\ Bracelet\)
\(\small \ P1455\ 搭配购买\)
\(\small \ P1616\ 疯狂的采药\)
\(\small \ P2722\ 总分 Score Inflation\)
\(\small \ P2918\ [USACO08NOV]买干草Buying\ Hay\)

前言：DP 快接触半年了。 还是想起来把曾经虐我的\(01背包\) 好好写写。

\[\large\ dp[i][j] \ = \ max(\ dp[i-1][j-w_i] \ + \ c_i \ , \ dp[i][j])\; \]

\[这个方程熟悉吗qwq \]

\[以及下面这个压维的。 \]

\[\large \ dp_j\ = \ max(\ dp[j-w_i] \ + \ c_i \ , \ dp_j)\; \]

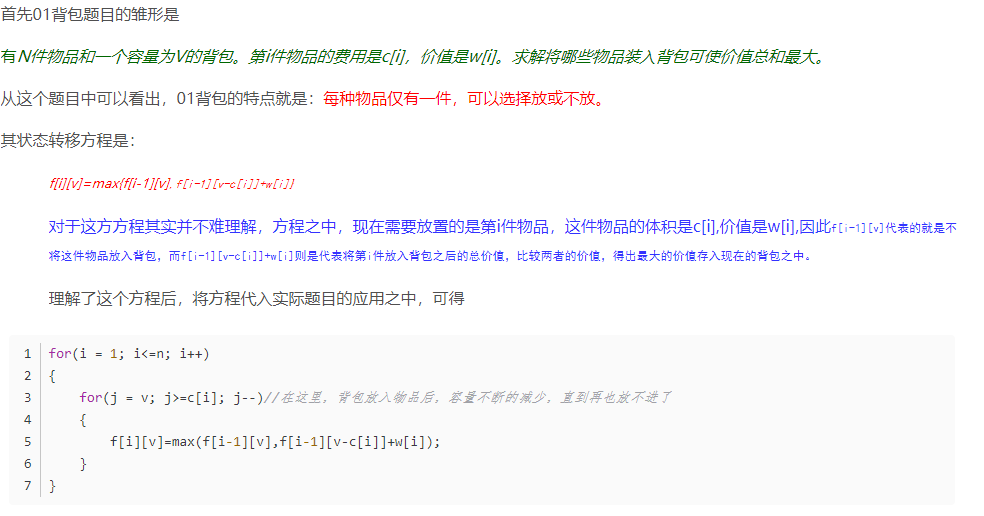
下面借鉴此处

其中\(F[i-1][j]\)表示前\(i-1\)件物品中选取若干件物品放入剩余空间为\(j\)的背包中所能得到的最大价值
而\(F[i-1][j-C_i]+W_i\)表示前\(i-1\)件物品中选取若干件物品放入剩余空间为\(j-C_i\)的背包中所能取得的最大价值加上第\(i\)件物品的价值
根据第 \(i\) 件物品放或是不放确定遍历到第 \(i\) 件物品时的状态\(F[i][j]\)
设物品件数为\(N\) 背包容量为\(V\) 第 \(i\)件物品体积为\(C_i\) 第\(i\)件物品价值为\(W_i\)

所以得出代码

for(register int i=1; i<=n; i++)
        for(register int j=m; j>=c[i]; j--) dp[i][j] = max(dp[i-1][j-c[i]] + w[i] , dp[i][j]) ;

\[F[i][j]只与F[i-1][j]和F[i-1][j-C_i]有关 \]

即只和\(i-1\)时刻状态有关 所以我们只需要用一维数组\(F[]\)来保存\(i-1\)时的状态\(F[]\)。
假设\(i-1\)时刻的\(F[]\)为\({a[0]\ a[1]\ a[2]… \ a[v]}\)
那么\(i\)时刻的\(F[]\)中第\(k\)个应该为\(max(a_k,a[k]-C[i]+W_i)\)
即 \(max(F_k,F[k-C_i]+W_i)\)
这就需要我们遍历\(V\)时逆序遍历
这样才能保证求 \(i\)时刻 \(F[k]\) 时 \(F[k-C_i]\) 是 \(i-1\) 时刻的值
如果正序遍历则当求\(F[k]\)时其前面的\(F_0\ F_1 \ F_k-1\)都已经改变过，里面存的都不是\(i-1\)时刻的值，这样求\(F_k\)时利用\(F[K-C_i]\)必定是错的值。最后\(F_v\)即为最大价值。
下面的完全背包会仔细解释为什么是倒序遍历（\(update\ on\ 4.13\)）

for(register int i=1; i<=n; i++)
	for(register int j=m; j>=c[i]; j--) dp[j] = max(dp[j-c[i]] + w[i] , dp[j]) ;

虽然时间复杂度不变 但是内存减少很多了。

=========================================update：大致模板

#include <bits/stdc++.h>
#define rep(i,j,n) for(register int i=j;i<=n;i++)
#define Rep(i,j,n) for(register int i=j;i>=n;i--)
#define low(x) x&(-x)
using namespace std ;
typedef long long LL ;
const int inf = INT_MAX >> 1 ;
inline LL In() { LL res(0) , f(1) ; register char c ;
#define gc c = getchar()
    while(isspace(gc)) ; c == '-' ? f = - 1 , gc : 0 ;
    while(res = (res << 1) + (res << 3) + (c & 15) , isdigit(gc)) ;
    return res * f ;
#undef gc
}

int n , m ;
const int N = 100000 + 5 ;
int f[N] ; //数组
inline void Ot() {
	n = In() , m = In() ;
	for(register int i=1;i<=n;i++) {
		int w = In() , c = In() ; //输入 体积&&价值
		for(register int j=m;j>=w;j--)
			f[j] = max(f[j] , f[j-w] + c) ; //状态转移方程
	}
	cout << f[m] << endl ; //f[m] 是 目标值。 所以输出。
}
signed main() {
//  freopen("test.in","r",stdin) ;
    return Ot() , 0 ;
}

可以根据这个代码来模拟过程。

=========================================例题。
P1048 采药
P1049 装箱问题
P1060 开心的金明
P1164 小A点菜
P2639 [USACO09OCT]Bessie的体重问题Bessie's We…
=========================================

P1048 采药

这题就比较裸了。直接套进去板子。

#include <bits/stdc++.h>
#define rep(i,j,n) for(register int i=j;i<=n;i++)
#define Rep(i,j,n) for(register int i=j;i>=n;i--)
#define low(x) x&(-x)
using namespace std ;
typedef long long LL ;
const int inf = INT_MAX >> 1 ;
inline LL In() { LL res(0) , f(1) ; register char c ;
#define gc c = getchar()
	while(isspace(gc)) ; c == '-' ? f = - 1 , gc : 0 ;
	while(res = (res << 1) + (res << 3) + (c & 15) , isdigit(gc)) ;
	return res * f ;
#undef gc
}

int T , M ;
const int N = 1000 + 5 ;
int dp[N] ;
inline void Ot() {
	T = In() , M = In() ;
	for(register int i=1;i<=M;i++) {
		int x = In() , y = In() ;
		for(register int j=T;j>=x;j--) dp[j] = max(dp[j-x]+y, dp[j]) ;
	}
	cout << dp[T] << endl ;
}
signed main() {
	return Ot() , 0 ;
}

P1049 装箱问题

这题转移方程略有不同。 重量就是价格（应该能这么理解）
所以 \(W[i] = C[i]\) 所以转移方程为\(dp[j]\ = \ max \ ( dp[j]\ ,\ dp[j-w[i]]\ +\ w[i]);\)

#include<bits/stdc++.h>
#define mx 25000
using namespace std;
int w[mx],n,V,dp[mx];
int main() {
	ios::sync_with_stdio(false);
	cin>>V>>n;
	for(int i=1; i<=n; i++) {
		cin>>w[i];
	}
	for(int i=1; i<=n; i++) {
		for(int j=V; j>=w[i]; j--) {
			dp[j]=max(dp[j],dp[j-w[i]]+w[i]);
		}
	}
	int ans=0;
	for(int i=1; i<=V; i++) {
		ans=max(ans,dp[i]);
	}
	cout<<V-ans<<'\n';
	return 0;
}

P1060 开心的金明

这题就是把模板套一下。 价值先预处理出来。

#include<bits/stdc++.h>
#define f(i,j,n) for(int i=j;i<=n;i++)
#define fa(i,j,n) for(int i=j;i>=n;i--)
using namespace std;
int w[30],v[30],f[50000];
int n,m;
int main() {
	cin>>m>>n;
	f(i,1,n) {
		cin>>v[i]>>w[i];
		w[i]*=v[i];
	}
	f(i,1,n)
		fa(j,m,v[i]) f[j]=max(f[j],f[j-v[i]]+w[i]);
	cout<<f[m]<<endl;
	return 0;
}

P1164 小A点菜

01背包的变式 \(f_j\ =\ f_j\ +\ f[j-w_i];\)

#include <bits/stdc++.h>
#define rep(i,j,n) for(register int i=j;i<=n;i++)
#define Rep(i,j,n) for(register int i=j;i>=n;i--)
#define low(x) x&(-x)
using namespace std ;
typedef long long LL ;
const int inf = INT_MAX >> 1 ;
inline LL In() { LL res(0) , f(1) ; register char c ;
#define gc c = getchar()
    while(isspace(gc)) ; c == '-' ? f = - 1 , gc : 0 ;
    while(res = (res << 1) + (res << 3) + (c & 15) , isdigit(gc)) ;
    return res * f ;
#undef gc
}

int n , m ;
const int N = 100 + 5 ;
const int M = 10000 + 5 ;
int w[N] ;
int f[M] ;
inline void Ot() {
	n = In() , m = In() ;
	for(register int i=1;i<=n;i++) w[i] = In() ;
	f[0] = 1 ;
	for(register int i=1;i<=n;i++)
		for(register int j=m;j>=w[i];j--) f[j] += f[j-w[i]] ;
	cout << f[m] << endl ;
}
signed main() {
//  freopen("test.in","r",stdin) ;
    return Ot() , 0 ;
}

P2639 [USACO09OCT]Bessie的体重问题Bessie's We…

重量就是价格
所以 \(W_i = C_i\) 所以转移方程为\(dp_j\ = \ max \ ( dp_j\ ,\ dp[j-w_i]\ +\ w_i);\)
但是这里赋值过了 所以就没什么关系了 直接跑\(01\)背包。

#include<iostream>
using namespace std;
int f[450001],w[100001],c[100001],n,m;
int main() {
    ios::sync_with_stdio(false);
    cin>>m>>n;
    for(int i=1; i<=n; i++) {
        cin>>c[i];
        w[i]=c[i];
    }
    for(int i=1; i<=n; i++) {
        for(int j=m; j>=c[i]; j--) {
            if(f[j-c[i]]+w[i]>f[j])
                f[j]=f[j-c[i]]+w[i]; //这里其实应该是max 当时就这么写了。
        }
    }
    cout<<f[m];
    return 0;
}

\[引入：01背包一般没有几个是裸题。 \]

\[一般会带有两个状态 如果是真的裸题一般就是普及-的难度（除非该题意思很难理解233 \]

\[两个状态就必须要用二维 \ 三维可能会爆内存 惨遭MLE 就GG了。em \]

\[两个状态 比如说一个是质量 一个是体积。n件物品。 \]

\[那么必须要把(F[N][M][V]) - > (F[M][V]) （其中M表示最大能承受的质量\ V表示最大能承受的体积） \]

=========================================二维例题。
P1794 装备运输_NOI导刊2010提高（04）
P1877 [HAOI2012]音量调节
P1910 L国的战斗之间谍
P2871 [USACO07DEC]手链Charm Bracelet
=========================================

P1794 装备运输_NOI导刊2010提高（04）

同上面说明

#include <bits/stdc++.h>
#define rep(i,j,n) for(register int i=j;i<=n;i++)
#define Rep(i,j,n) for(register int i=j;i>=n;i--)
#define low(x) x&(-x)
using namespace std ;
typedef long long LL ;
const int inf = INT_MAX >> 1 ;
inline LL In() { LL res(0) , f(1) ; register char c ;
#define gc c = getchar()
    while(isspace(gc)) ; c == '-' ? f = - 1 , gc : 0 ;
    while(res = (res << 1) + (res << 3) + (c & 15) , isdigit(gc)) ;
    return res * f ;
#undef gc
}

int v , g ;
int n ;
const int N = 500 ;
int dp[N][N] ;
inline void Ot() {
	v = In() ;
	g = In() ;
	n = In() ;
	for(register int i=1;i<=n;i++) {
		int c = In() ;
		int x = In() , y = In() ;
		for(register int j=v;j>=x;j--)
			for(register int k=g;k>=y;k--) dp[j][k] = max(dp[j][k] , dp[j-x][k-y] + c) ;
	}
	cout << dp[v][g] << endl ;
}
signed main() {
//  freopen("testdata.txt","w",stdout) ;
    return Ot() , 0 ;
}

P1877 [HAOI2012]音量调节

这题在某谷上写过\(题解\) 了。

#include <bits/stdc++.h>
#define rep(i,j,n) for(register int i=j;i<=n;i++)
using namespace std;
typedef long long LL;
inline LL read(){ LL x=0;int f(1);char ch=getchar();
	while(!isdigit(ch)) { if(ch=='-') f=-1;
		ch=getchar();
	}
	while(isdigit(ch)) x=(x<<1)+(x<<3)+(ch^48),ch=getchar(); return x*f;
}

int n;
int Begin,Max;
int a[1<<6];
int dp[1<<6][1<<12];
signed main(){
	memset(dp,0,sizeof(dp));
	n=read(); Begin=read(); Max=read();
	dp[0][Begin]=1;
	rep(i,1,n) a[i]=read(); 
	rep(i,1,n) rep(j,0,Max)  {
		if (j+a[i] <= Max) dp[i][j]=dp[i][j]||dp[i-1][j+a[i]];
		if (j-a[i] >= 0)   dp[i][j]=dp[i][j]||dp[i-1][j-a[i]];
	}
	LL ans = -0x7f;
	for(register int i=1;i<=Max;i++) {
		if(dp[n][i]) ans = i;
	}
	if ( ans != -0x7f) cout << ans << endl ;
	else puts("-1") ; 
	return 0;
}

P1910 L国的战斗之间谍

根据上面这部分。 把几个变量整合到一块。

#include <bits/stdc++.h>
#define rep(i,j,n) for(register int i=j;i<=n;i++)
#define Rep(i,j,n) for(register int i=j;i>=n;i--)
#define low(x) x&(-x)
using namespace std ;
typedef long long LL ;
const int inf = INT_MAX >> 1 ;
inline LL In() { LL res(0) , f(1) ; register char c ;
#define gc c = getchar()
	while(isspace(gc)) ; c == '-' ? f = - 1 , gc : 0 ;
	while(res = (res << 1) + (res << 3) + (c & 15) , isdigit(gc)) ;
	return res * f ;
#undef gc
}


int v , m ;
int n ;
const int N = 1000 + 5 ;
int dp[N][N] ;

inline void Ot() {
	n = In() ;
	v = In() , m = In() ;
	rep(i,1,n) {
		int x = In() , y = In() , z = In() ;
		Rep(i,v,y)
			Rep(j,m,z) dp[i][j] = max(dp[i-y][j-z] + x , dp[i][j]) ;
	}
	cout << dp[v][m] << endl ;
}
signed main() {
	return Ot() , 0 ;
}

P2871 [USACO07DEC]手链Charm Bracelet

#include <bits/stdc++.h>
#define rep(i,j,n) for(register int i=j;i<=n;i++)
#define Rep(i,j,n) for(register int i=j;i>=n;i--)
#define low(x) x&(-x)
using namespace std ;
typedef long long LL ;
const int inf = INT_MAX >> 1 ;
inline LL In() { LL res(0) , f(1) ; register char c ;
#define gc c = getchar()
	while(isspace(gc)) ; c == '-' ? f = - 1 , gc : 0 ;
	while(res = (res << 1) + (res << 3) + (c & 15) , isdigit(gc)) ;
	return res * f ;
#undef gc
}


int v , m ;
int n ;
const int N = 400 + 5 ;
int dp[N][N] ;

inline void Ot() {
	v = In() , m = In() ;
	n = In() ;
	rep(i,1,n) {
		int x = In() , y = In() , z = In() ;
		Rep(i,v,x)
			Rep(j,m,y) dp[i][j] = max(dp[i-x][j-y] + z , dp[i][j]) ;
	}
	cout << dp[v][m] << endl ;
}
signed main() {
	return Ot() , 0 ;
}

带点[并查集]的

P1455 搭配购买

#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
inline LL read () { LL res = 0 ;int f (1) ;char ch = getchar ();
    while (!isdigit(ch)) { if (ch == '-') f = -1 ;ch = getchar();}
    while (isdigit(ch)) res = (res << 1) + (res << 3) + (ch ^ 48) ,ch = getchar(); return res * f ;
}
int n,m,we,fa[10005],w[10005],c[10005],dp[10005];
inline int find(int x){
    if(fa[x]!=x) fa[x]=find(fa[x]);
    return fa[x];
}
inline void merge(int x,int y){
    int f1=find(x),f2=find(y);
    if(f1!=f2)fa[f1]=f2,c[f2]+=c[f1],w[f2]+=w[f1];
}
int main(){
    n=read(),m=read(),we=read();
    for(register int i=1;i<=n;i++) fa[i]=i;
    for(register int i=1;i<=n;i++) c[i]=read(),w[i]=read();
    for(register int i=1;i<=m;i++){
        int u=read(),v=read();
        merge(u,v);
    }
    for(register int i=1;i<=n;i++) if(fa[i]==i)
    for(register int j=we;j>=c[i];j--) dp[j]=max(dp[j],dp[j-c[i]]+w[i]);
    cout << dp[we] << endl ;
    return 0;
}

以及这道题
还有在这道题

\[HDU的01背包多得是 \]

HDU - 2026 - Bone Collector
HDU - 2546 - 饭卡
HDU - 2955 - Robberies
HDU - 1203 - I NEED A OFFER!
HDU - 1171 - Big Event in HDU

====================================================完全背包。（\(update\ on\ 4.13\)）

那么我们再次仔细思考。 为什么01背包要反过来？
就假设是正过来的好了吖。
正序遍历 是 \(for(register\ int\ i \ =\ w[i];i<=m;i++)\)
根据循环条件 我们可以得知 \(w_i\) 可以放 \(inf\) 次（假设\(m=∞\)）
这样子的话。就是完全背包。
\(∵01背包一件物品只能放一次\)
\(∴就只能更新一次值\ 所以是\ from\ w_i \ to \ m\)

=========================================例题。
P1616 疯狂的采药
P2722 总分 Score Inflation
\(P2918\ [USACO08NOV]买干草Buying\ Hay\)
=========================================

P1616 疯狂的采药

内循环倒过来。 因为这是一个完全背包（也是01背包的变式
在 <采药> 中，每种草药只允许 采一次 。（所以是标准的01背包 上面也有了。
我们将采 第\(i\)种草药 所需的 时间 设为 \(t_i\) 价值 设为 \(p_i\)
如果有一个数组 \(f[i][j]\) 来表示 从前往后 到第\(i\)种草药 (当然前面可能有草药不采) ，花费了最多 \(j\) 时间 (意思是可能花费了少于\(j\)时间) 时 能采到草药的 最大价值
到第\(i\)种草药时有两种情况：采与不采。
若不采这种草药，则 时间花费没有增多 ，经过的 草药种数增加了\(1\) ， 采到草药价格不变 ，所以 \(f[i][j]=f[i-1][j]\) ；
若采这种草药 则 时间花费增加了\(t_i\) 种数增加\(1\) 采到草药价格增加了\(p_i\)，所以 \(f[i][j]=f[i-1][j-t_i]+p_i\) 。
我们当然要使 \(f[i][j]\)尽可能大 即有 \(f[i][j]=max(f[i-1][j],f[i-1][j-t_i]+p_i)\)

#include <bits/stdc++.h>
#define rep(i,j,n) for(register int i=j;i<=n;i++)
#define Rep(i,j,n) for(register int i=j;i>=n;i--)
#define low(x) x&(-x)
using namespace std ;
typedef long long LL ;
const int inf = INT_MAX >> 1 ;
inline LL In() { LL res(0) , f(1) ; register char c ;
#define gc c = getchar()
    while(isspace(gc)) ; c == '-' ? f = - 1 , gc : 0 ;
    while(res = (res << 1) + (res << 3) + (c & 15) , isdigit(gc)) ;
    return res * f ;
#undef gc
}

int t , m ;
const int T = 100000 + 5 ;
LL f[T] ;
inline void Ot() {
	t = In() , m = In() ;
	rep(i,1,m) {
		int x = In() , y = In() ;
		rep(j,x,t) f[j] = max(f[j] , f[j-x] + y) ;
	}
	cout << f[t] << endl ;
}
signed main() {
//  freopen("test.in","r",stdin) ;
    return Ot() , 0 ;
}

P2722 总分 Score Inflation

这和P1616 疯狂的采药 基本是一样的
都是完全背包。

#include<bits/stdc++.h>
#define f(i,j,n) for(int i=j;i<=n;i++)
using namespace std;
int V, n;
int a[10001],b[10001],f[10001];
void read(int &x) {
    int f=1;
    x=0;
    char s=getchar();
    while(s<'0' or s>'9') {
        if(s=='-') f=-1;
        s=getchar();
    }
    while(s>='0' and s<='9') {
        x=x*10+s-'0';
        s=getchar();
    }
    x*=f;
}
int main() {
    read(V),read(n);
    f(i,1,n) read(a[i]),read(b[i]);
    f(j,1,n)
    f(k,b[j],V) f[k]=max(f[k],f[k-b[j]]+a[j]);
    cout<<f[V]<<endl;
    return 0;
}

\(P2918\ [USACO08NOV]买干草Buying\ Hay\)

这题就有点坑了。
坑点1 ：要用最小值。所以初值赋值最大值。 但是 \(dp_0 = 0\) 不然如何都是 最大值
坑点2 ：目标不是\(dp_h\) 而是 \(max\) \(dp_h...dp_{h+5000}\) 因为

第\(i\)公司卖的干草包重量 为\(P_i (1<=P_i<=5000)\)磅，需要的开销为\(C_i (1<C_i <=5000)\)美元
没准 多一丢丢还便宜点。（大雾。

\(code\)

#include <bits/stdc++.h>
#define rep(i,j,n) for(register int i=j;i<=n;i++)
#define Rep(i,j,n) for(register int i=j;i>=n;i--)
#define low(x) x&(-x)
using namespace std ;
typedef long long LL ;
const int inf = INT_MAX >> 1 ;
inline LL In() { LL res(0) , f(1) ; register char c ;
#define gc c = getchar()
    while(isspace(gc)) ; c == '-' ? f = - 1 , gc : 0 ;
    while(res = (res << 1) + (res << 3) + (c & 15) , isdigit(gc)) ;
    return res * f ;
#undef gc
}

int n , h ;
const int N = 55000 + 5 ;
int dp[N] ;
inline void Ot() {
	n = In() , h = In() ;
	memset(dp,0x7f,sizeof(dp)) ;
	dp[0] = 0 ;
	rep(i,1,n) {
		int x = In() , y = In() ;
		rep(j,x,h+5000) dp[j] = min(dp[j] , dp[j-x] + y) ;
	}
	int ans = 0x7f7f7f7f7f ;
	rep(i,h,h+5000) ans = min(ans , dp[i]) ;
	cout << ans << endl ;
}
signed main() {
//  freopen("test.in","r",stdin) ;
    return Ot() , 0 ;
}