多项式笔记
多项式笔记
本文为阅读 OI-Wiki 书籍 学长slide 网上博客的笔记
多项式一般用来对一些函数的计算加速。
前置知识
多项式插值
\(n + 1\) 个横坐标互不相同的点可以唯一确定一个 \(n\) 次多项式。
复数
复数运算
已知 \(i^2 = -1\)， 那么复数加减乘除全部就可以自己手推出来。
辐角和模长
复数的模与辐角是复数三角形式表示的两个基本元素，复数所对应的向量长度称为复数的幅值，该向量与实轴正方向的夹角为复数的辐角。辐角的大小有无穷多，但是辐角主值唯一确定。利用复数的模和辐角，可以将复数表示成三角表示式和指数表示式，并可以和代数表示式之间互相转化，以方便讨论不同问题时的需要。 ----百度百科
复数表示
代数表示法： \(z = x + yi\)
由辐角和模长定义可知三角表示法： $$z = r(cos\theta + isin\theta)$$
由欧拉公式可知 $$ e^{i\theta }=\cos \theta +i\sin \theta $$
指数表示法：\(z = re^{i\theta}\)
从指数表示法我们就可以看出， 复数乘法就是模长相乘， 辐角相加。
单位根
引理1：任意一个复数系一元 \(n\) 次多项式方程在复数域上恰好 \(n\) 个根。
我们记 \(x^n - 1 = 0\) 的 \(n\) 个根分别记为 \(w_0, w_1...w_{n - 1}\)。
\(w_{i}=\cos \dfrac{2i\pi }{n}+i\sin \dfrac{2i\pi }{n}\)
这式子可以从复数乘法的几何意义来来理解， 模长必定为1， 辐角乘 \(n\) 以后要与 \(x\) 轴正半轴重合， 所以单位就是把单位圆切割为正多边形的顶点。
性质：
这些性质的证明： 都可以通过几何意义来理解。
快速傅里叶变换 FFT
算法思路
我们知道 \(F(x)\) 和 \(G(x)\)， 我们要求 \(H(x) = F(x)G(x)\)， 考虑暴力的话就是卷积 \(O(n^2)\)， 为了避免卷积， 我们考虑插值， 如果插值的话， 就有 \(\forall_i H(x_i) = F(x_i)G(x_i)\)。
但现在就有一个问题， 我们怎么实现快速插值并且将插值快速变换为多项式呢？
DFT
考虑我们要快速求出某个函数 \(f(x)\) 在 \(x\) 取值为 \(\begin{Bmatrix}w_n^0, w_n^1...w_n^n\end{Bmatrix}\) 的值 \(F = \begin{Bmatrix}y_0, y_1...y_n \end{Bmatrix}\)。 则我们有 \(F(x) = \sum_{i = 0}^{n}f_ix^i\)。 我们想要快速求出 \(F\) 函数， 可以这么做：
将 \(F(x)\) 将系数 \(f_i\) 按 \(x\) 奇偶分类则有：
考虑单位根有这样的性质， $\large ( w_n^k )^2 = w_n^2k = w_{ \frac{n}{2} }^k $
和：
考虑我们用总共 \(n\) 个插值（包含 \(G\) 和 \(H\) 个 \(\frac{n}{2}\) 个）， 就可以求出 \(f\) 的 \(n\) 个插值， 本来我们暴力插值的话 一个插值 \(O(n)\) 总共 \(n^2\)， 现在我们递归到 \(n = 1\) 是就可以 \(O(1)\) 算插值， 然后递归上来， 就可以在 \(O(nlogn)\) 的时间复杂度算出 \(f\) 的 \(n\) 个插值。
IDFT
现在我们要从插值还原到多项式的系数。
考虑从线性代数的角度理解：
左边向量为插值， 右边向量为系数。 考虑我们要求出系数， 就是给插值向量左乘一个 \(w\) 的逆矩阵。 逆矩阵就是 \(w_i^j\) 的倒数再除以 \(n\)， 所以我们再把 \(y_i\) 当成一个新函数的系数， 以 $$\large\frac{1}{w_n^0 n}, \frac{1}{w_n^1 n}...$$ 为 \(x\) 的插值算出来就是系数。
考虑 \(w_n^i\) 的倒数就等于 \(\large\frac{1}{\omega_k}=\omega_k^{-1}=\mathrm{e}^{-\frac{2\pi \mathrm{i}}{k}}=\cos\left(\frac{2\pi}{k}\right)+\mathrm{i} \sin\left(-\frac{2\pi}{k}\right)\)。 所以我们只需要在 DFT 的代码上更改一个地方即可。
代码
点击查看代码
#include<bits/stdc++.h>
using namespace std;
typedef double db;
const db pi = acos(-1);
const int N = 3e6 + 10;
struct C{
db x, y;
C() { x = y = 0; }
C(db _x, db _y) : x(_x), y(_y) {}
inline C operator + (const C &a) { return C(x + a.x, y + a.y); }
inline C operator - (const C &a) { return C(x - a.x, y - a.y); }
inline C operator * (const C &a) { return C(x * a.x - y * a.y, x * a.y + y * a.x); }
};
int n, m, lim, bit, rev[N];
void FFT(vector<C> &v, int op) {
for(int i = 0; i < lim; i++) if(i < rev[i]) swap(v[i], v[rev[i]]);
for(int k = 1; k < lim; k <<= 1) {
C omega(cos(pi / k), op * sin(pi / k));
for(int i = 0; i < lim; i += (k << 1)) {
C w(1, 0);
for(int j = 0; j < k; j++, w = w * omega) {
C s = v[i + j], t = v[i + j + k] * w;
v[i + j] = s + t, v[i + j + k] = s - t;
}
}
}
if(op == -1) for(int i = 0; i < lim; i++) v[i].x /= lim;
}
int main() {
scanf("%d%d", &n, &m);
lim = 1 << (32 - __builtin_clz(n + m)), bit = 32 - __builtin_clz(n + m);
vector<C> A(lim), B(lim);
for(int i = 0; i <= n; i++) scanf("%lf", &A[i].x);
for(int i = 0; i <= m; i++) scanf("%lf", &B[i].x);
for(int i = 0; i < lim; i++) rev[i] = (rev[i >> 1] >> 1) | ((i & 1) << (bit - 1));
FFT(A, 1); FFT(B, 1);
for(int i = 0; i < lim; i++) A[i] = A[i] * B[i];
FFT(A, -1);
for(int i = 0; i <= n + m; i++) printf("%lld ", (long long)(A[i].x + 0.5));
return 0;
}
快速数论变换 NTT
NTT 和 FFT 十分相似， 常见于多项式计算需要取模时使用， 考虑在 \(mod p\) 意义下的原根的具有和单位根相似的性质，也就是构成一个循环节。
其他和FFT非常类似， 就不写了。
多项式牛顿迭代
泰勒展开
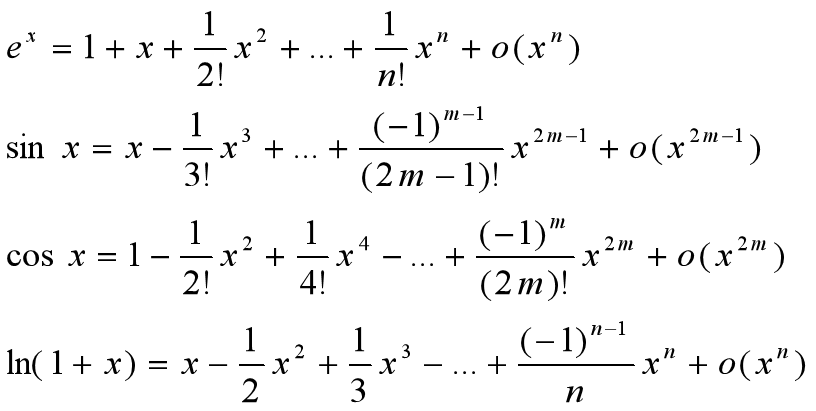
就是一个用多项式逼近某个函数的公式， 非常的牛， 我也不会， 背住就好了。
牛顿迭代解决这样的一个问题：
给定多项式 \(g\left(x\right)\)，已知有 \(f\left(x\right)\) 满足：
求出模 \(x^{n}\) 意义下的 \(f\left(x\right)\)。
算法
from OI_WIKI
将 \(g\left(f\left(x\right)\right) 在 f_{0}\left(x\right)\) 处进行泰勒展开，有：
因为 \(f\left(x\right)-f_{0}\left(x\right)\) 的最低非零项次数最低为 \(\left\lceil\frac{n}{2}\right\rceil\)，故有：
则：
这里需要求导：
所以比较常用的是这几个：
\(a' = 0\)
\((x^a)' = a(x^{a - 1})\)
\((a^x)' = (a^x)lna\)
\((log_ax)' = \large\frac{1}{xlna}\)
复合函数求导： \(f'(g(x)) = f'(g(x)) * g'(x)\)
多项式求逆
\(h(x)\) 给定。
带入公式即可。
多项式开根
多项式求导
就按照上面的求导规则即可， \((ax^2 + bx)' = (ax^2)' + (bx)'\)。
多项式积分
把求导反着来。
多项式ln
\((lnf(x))' = \frac{1}{f(x)}\)， 我们求个导再求个逆元再积分即可。
多项式exp
快速沃尔什变换 FWT
给两个长为 \(2^n\) 的序列 \(A\)， \(B\)。 我们规定 \(A \times B = C\) 的运算规则是：
\(\bigotimes\) 常见的是 or， and， xor。 我们需要在 \(nlogn\) 时间得到 \(C\)， 这里的 \(n\) 指 \(2^n\)。
我们参照 FFT， 通过插值来变换， 但是这里显然不能插值， 但是我们可以借鉴思想。 构造某种变换， 使得其可以快速变换和反演， 这也是算法精髓所在。
or
接下来我们讲 or 的做法。
我们构造 \(FWT[a]_i\) 表示通过序列 \(a\) 得出的 \(FWT[a]\) 序列， \(i\) 就是下标， 考虑 \(FWT[a]_i = \sum_{i or j = i} a_j\)，
那么我们就有 \(FWT[a]_i * FWT[b]_i = FWT[c]_i\)， 证明也很简单， 就不写了。
那么现在就考虑怎么快速得到 \(FWT[a]\)， 我们可以根据下标的二进制把 \(FWT\) 分治， 分成以最高位为 \(1\) \(a1\)， 和最高位为 \(0\) \(a0\) 的两段， 考虑边界就是每段长度为 1， 可以轻松得到， 现在我们就考虑怎么通过这两段分别的FWT推出一整段的FWT， 考虑\(FWT[a] = merge(FWT[a0], FWT[a0] + FWT[a1])\)， 因为我们要枚举后半段的子集， 后半段的子集可以分为最高位为 1， 后面的随便选， 和最高位为 0， 后面的随便选。
现在我们就考虑怎么将 \(FWT[a]\) 还原回 \(a\)， 考虑我们怎么从 \(a\) 来的， 其实就是FWT的逆过程， 我们把 \(FWT[a] 还原成FWT[a0] 和 FWT[a1]\) 再递归下去， 等到长度为 1 就可以直接是 \(a\)了。
那么就是 \(FWT[a0]\) 不变， \(FWT[a1] = FWT[a] - FWT[a0]\)， 这里 \(FWT[a]\) 取后半段。
void OR(int *v, int type = 1) {
for(int lim = 2, k = 1; lim <= n; lim <<= 1, k <<= 1)
for(int i = 0; i < n; i += lim)
for(int j = 0; j < k; j++)
v[i + j + k] = add(v[i + j + k], mul(v[i + j], type));
}
参考代码理解， 写的迭代形式。
and
考虑仿照上面的做法， \(FWT[a]_i\) 就是 \(\sum_{i and j = i} a_j\)， \(FWT[a] = merge(FWT[a1] + FWT[a0], FWT[a1])\)。
xor
对于 xor， \(FWT[a] = merge(FWT[a0] + FWT[a1], FWT[a0] - FWT[a1])\)
拉格朗日插值法
如果 $$
