NEERC 2016-2017 Probelm G. Game on Graph

NEERC 2016-2017 Probelm G. Game on Graph

Description

　　Gennady and Georgiy are playing interesting game on a directed graph. The graph has n vertices and m arcs, loops are allowed. Gennady and Georgiy have a token placed in one of the graph vertices. Players take turns moving the token along one of the arcs that starts in the vertex the token is currently in. When there is no such arc, then this player loses the game.

　　For each initial position of the token and the player who is moving first, your task is to determine what kind of result the game is going to have. Does it seem to be easy? Not so much.

　　On one side, Gennady is having a lot of fun playing this game, so he wants to play as long as possible. He even prefers a strategy that leads to infinite game to a strategy that makes him a winner. But if he cannot make the game infinite, then he obviously prefers winning to losing.

　　On the other side, Georgiy has a lot of other work, so he does not want to play the game infinitely.
Georgiy wants to win the game, but if he cannot win, then he prefers losing game to making it infinite.
Both players are playing optimally. Both players know preferences of the other player.

Input

　　In the first line there are two integers — the number of vertices n (1 ≤ n ≤ 100 000) and the number of arcs m (1 ≤ m ≤ 200 000). In the next m lines there are two integers a and b on each line, denoting an arc from vertex a to vertex b. Vertices are numbered from 1 to n. Each (a, b) tuple appears at most once.

Output

　　In the first line print n characters — i-th character should denote the result of the game if Gennady starts in vertex i. In the second line print n characters — i-th character should denote the result of the game if Georgiy starts in vertex i. The result of the game is denoted by “W” if the starting player wins the game, “L” if the starting player loses the game, and “D” (draw) if the game runs infinitely.

Example

6 7
1 2
2 1
2 3
1 4
4 1
4 5
5 6
WDLDWL
DWLLWL

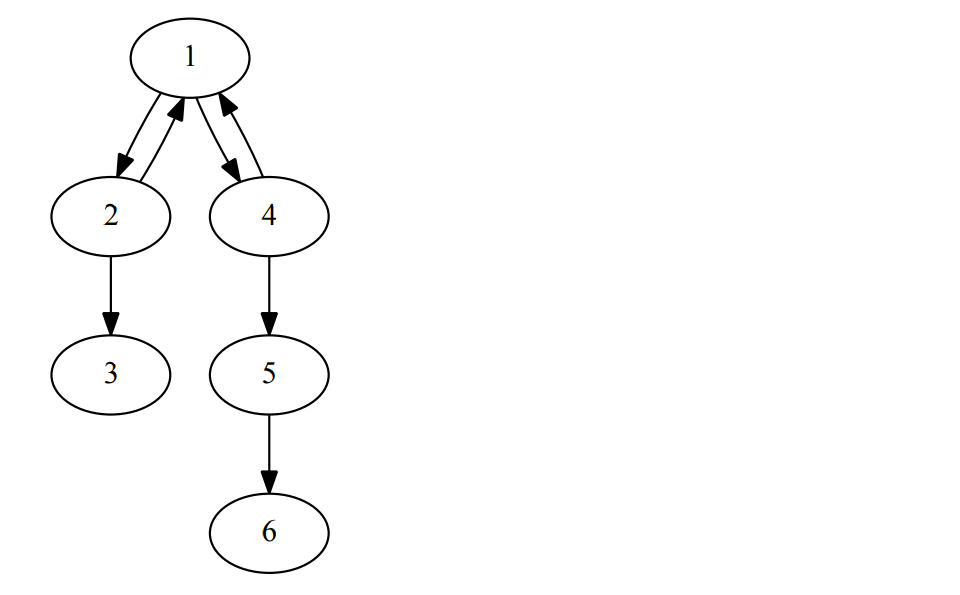
Note

　　In vertices 3 and 6 the game is already lost. In vertex 5, the only move is to vertex 6, and the player wins. If Georgiy starts in vertex 1, or Gennady in vertices 2 or 4, Gennady can always go to vertex 1, and make the game infinite. If Georgiy starts in vertex 4, he can either go to vertex 1 (which leads to a draw) or to vertex 5, which leads to losing. Georgiy prefers the latter. Similarly, from vertex 2, he prefers to go to 3 and win. From vertex 1, Gennady can go to vertex 2 and lose, or go to vertex 4 and win. He prefers the latter.

做法:

　　首先这道题特殊的地方在于玩家二的特殊要求, 对它来说输比平局要好.所以我们在利用后继状态确立胜负的时候, 就要做出一些改变.

• 对于玩家二为先手来说, 如果一个状态的后继状态有一个不为平局, 那么一定不为平局.
• 对于玩家一为先手来说, 如果一个状态的后继状态都不为平局, 其一定不为平局.
  　　先利用拓扑排序确立出平局状态, 平局状态一定不会出现在拓扑序中.接着标记出所有的胜负状态, 剩下那些没有被标记的就是可能为平局状态, 但是因为玩家二的特殊, 所以这些状态一定是玩家一胜利.