树链剖分
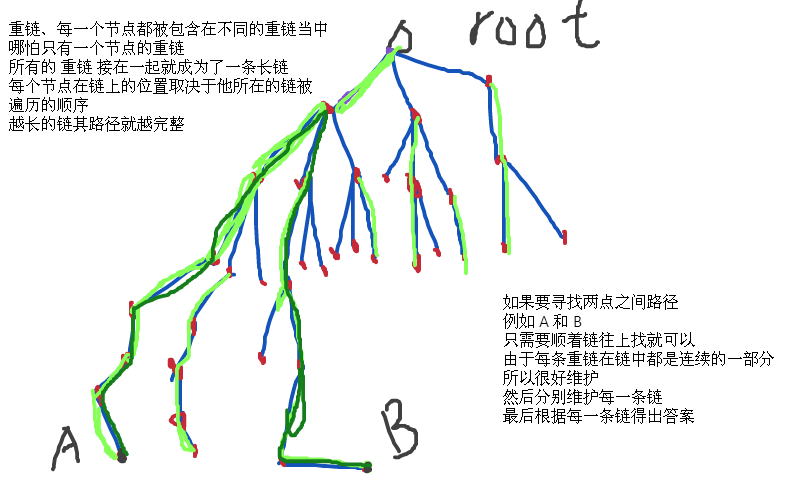
树链剖分简述
把一棵树剖分为若干条链,然后利用数据结构
(树状数组,SBT,Splay,线段树等等)去维护每一条链,复杂度为O(logn)
第一步:对树进行轻重链的划分
定义size( x )为以 x 为根节点的子树的节点个数
令 v 为 u 的儿子中size()值最大的节点
,那么边( u , v )就是重边,其余同深度的边为轻边
有两条重要的性质
(1) 在轻边 ( u , v )中size( v )<=size( v )/2
(2) 在根节点到某点的路径中,
有不超过 logn 条轻边和 logn 条重路径
剖分过程分为两次 bfs 或者 两次 dfs
如果是两次 dfs
第一次 dfs 为记录所有重边
第二次 dfs 为连接重边形成重链
具体过程就是以根节点为起点,拉着重边向下扩展
不在当前重链上的节点,以该节点为起点向下重新拉一条重链
剖分完毕后,每条重链都相当于一段区间
然后用数据结构去维护每一段区间
把所有重链首尾相连,放到数据结构上,然后维护整体
这里会用到很多数组
介绍其作用
size [] : 保存以节点为根的子节点个数
top [] : 保存当前节点所在的重链的顶端节点的编号
son [] : 保存节点的重儿子的编号
dep[] : 保存当前节点的深度
fath[] : 保存父亲节点的编号
tid [] : 保存树中每个节点剖分后的新编号
rank[] : 保存节点在线段树中的位置
代码 :剖分
void dfs1(int u,int father,int d)
{
dep[u]=d;
fa[u]=father;
siz[u]=1;
for(int i=head[u];~i;i=next[i])
{
int v=to[i];
if(v!=father)
{
dfs1(v,u,d+1);
siz[u]+=siz[v];
if(son[u]==-1||siz[v]>siz[son[u]])
son[u]=v;
}
}
}
void dfs2(int u,int tp)
{
top[u]=tp;
tid[u]=++tim;
rank[tid[u]]=u;
if(son[u]==-1) return;
dfs2(son[u],tp);
for(int i=head[u];~i;i=next[i])
{
int v=to[i];
if(v!=son[u]&&v!=fa[u])
dfs2(v,v);
}
}
P3384 【模板】树链剖分
题目描述
如题,已知一棵包含N个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
操作1: 格式: 1 x y z 表示将树从x到y结点最短路径上所有节点的值都加上z
操作2: 格式: 2 x y 表示求树从x到y结点最短路径上所有节点的值之和
操作3: 格式: 3 x z 表示将以x为根节点的子树内所有节点值都加上z
操作4: 格式: 4 x 表示求以x为根节点的子树内所有节点值之和
输入输出格式:
第一行包含4个正整数N、M、R、P,分别表示树的结点个数、操作个数、根节点序号和取模数(即所有的输出结果均对此取模)。
接下来一行包含N个非负整数,分别依次表示各个节点上初始的数值。
接下来N-1行每行包含两个整数x、y,表示点x和点y之间连有一条边(保证无环且连通)
接下来M行每行包含若干个正整数,每行表示一个操作,格式如下:
操作1: 1 x y z
操作2: 2 x y
操作3: 3 x z
操作4: 4 x
输出格式:
输出包含若干行,分别依次表示每个操作2或操作4所得的结果(对P取模)
输入输出样例
输入样例#1:
5 5 2 24
7 3 7 8 0
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3
输出样例#1:
2
21
说明
时空限制:1s,128M
数据规模:
对于30%的数据:N<=10,M<=10
对于70%的数据:N<=1000,M<=1000
对于100%的数据:N<=100000,M<=100000
(其实,纯随机生成的树LCA+暴力是能过的,可是,你觉得可能是纯随机的么233)
样例说明:
树的结构如下:
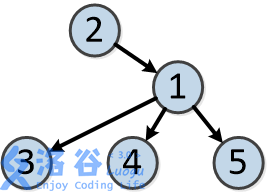
各个操作如下:

故输出应依次为2、21(重要的事情说三遍:记得取模)
#include<cstdio>
#include<cstring>
#include<iostream>
#define N 150000
#define For(i,x,y) for(int i=x;i<=y;++i)
#define lson(x) (x<<1)
#define rson(x) ((x<<1)+1)
using namespace std;
typedef long long LL;
int n,m,r,M;
struct Tree{
LL l[N*4],r[N*4],w[N*4],sum[N*4];
void upd(int x){sum[x]=(sum[lson(x)]+sum[rson(x)]+w[x]*(r[x]-l[x]+1))%M;}
void build(int p,int L,int R) {
l[p]=L;r[p]=R;w[p]=0;
if(L==R)return;
int MID=(L+R)>>1;
build(lson(p),L,MID);
build(rson(p),MID+1,R);
}
void ins(int p,int x,int v) {
int L=l[p],R=r[p];int MID=(L+R)>>1;
if(L==R){
w[p]+=v;w[p]%=M;upd(p);return;
}
if(x<=MID)ins(lson(p),x,v);
else ins(rson(p),x,v);
upd(p);
}
void add(int x,int L,int R,int v){
int mid=(l[x]+r[x])>>1;
if(l[x]==L&&r[x]==R)
{
w[x]+=v;w[x]%=M;upd(x);return;
}
if(R<=mid)add(lson(x),L,R,v);
if(L>mid)add(rson(x),L,R,v);
if(R>mid&&L<=mid){
add(lson(x),L,mid,v);
add(rson(x),mid+1,R,v);
}
upd(x);
}
int getsum(int x,int L,int R){
int mid=(l[x]+r[x])>>1;int tans=w[x]*(R-L+1)%M;
if(l[x]==L&&r[x]==R)
return sum[x];
if(R<=mid)return (getsum(lson(x),L,R)+tans)%M;
if(L>mid)return (getsum(rson(x),L,R)+tans)%M;
if(R>mid&&L<=mid)
return (getsum(lson(x),L,mid)+getsum(rson(x),mid+1,R)+tans)%M;
}
}T;
struct Graph{
struct E{
int next,to;
}edge[N*2];
int head[N];int cnt;
bool vis[N];LL v[N],size[N],son[N],top[N],id[N],deep[N],fa[N],xid[N];
int sign;
void adde(int u,int v){
edge[++cnt].to=v;edge[cnt].next=head[u];head[u]=cnt;
edge[++cnt].to=u;edge[cnt].next=head[v];head[v]=cnt;
}
void dfs1(int u){
size[u]=1;int S=0;
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;
if(vis[v])continue;vis[v]=1;
deep[v]=deep[u]+1;fa[v]=u;
dfs1(v);
size[u]+=size[v];
if(!S||size[v]>size[S])S=v;
}
son[u]=S;
}
void dfs2(int u,int tp){
id[u]=++sign;
top[u]=tp;
if(!son[u]){xid[u]=sign;return;}
vis[son[u]]=1;
dfs2(son[u],tp);
for(int i=head[u];i;i=edge[i].next){
int v=edge[i].to;if(vis[v])continue;
vis[v]=1;dfs2(v,v);
}
xid[u]=sign;
}
void prework(){
cin>>n>>m>>r>>M;
For(i,1,n)scanf("%d",&v[i]);
For(i,1,n-1)
{
int u,v;scanf("%d%d",&u,&v);
adde(u,v);
}
vis[r]=1;
dfs1(r);
memset(vis,0,sizeof(vis));
vis[r]=1;
dfs2(r,r);
T.build(1,1,n);
For(i,1,n)T.ins(1,id[i],v[i]);
}
void add1(int u,int v,int w){
if(deep[top[u]]<deep[top[v]])swap(u,v);
while(top[u]!=top[v]){
T.add(1,id[top[u]],id[u],w);
u=fa[top[u]];
if(deep[top[u]]<deep[top[v]])swap(u,v);
}
if(deep[u]<deep[v])swap(u,v);
T.add(1,id[v],id[u],w);
}
int get(int u,int v){
int ans=0;
if(deep[top[u]]<deep[top[v]])swap(u,v);
while(top[u]!=top[v]){
ans=(ans+T.getsum(1,id[top[u]],id[u]))%M;
u=fa[top[u]];
if(deep[top[u]]<deep[top[v]])swap(u,v);
}
if(deep[u]<deep[v])swap(u,v);
ans=(ans+T.getsum(1,id[v],id[u]))%M;
return ans%M;
}
void add2(int u,int w){
T.add(1,id[u],xid[u],w);
}
int get2(int u){
return T.getsum(1,id[u],xid[u])%M;
}
}G;
int main(){
G.prework();
For(t,1,m){
int opt;
scanf("%d",&opt);
int u,v,w;
if(opt==1){
scanf("%d%d%d",&u,&v,&w);
G.add1(u,v,w);
}
if(opt==2){
scanf("%d%d",&u,&v);printf("%d\n",G.get(u,v));
}
if(opt==3){
scanf("%d%d",&u,&w);G.add2(u,w);
}
if(opt==4){
scanf("%d",&u);printf("%d\n",G.get2(u));
}
}
return 0;
}


【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】凌霞软件回馈社区,博客园 & 1Panel & Halo 联合会员上线
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】博客园社区专享云产品让利特惠,阿里云新客6.5折上折
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步