Codeforces Round 927 (Div. 3)
A
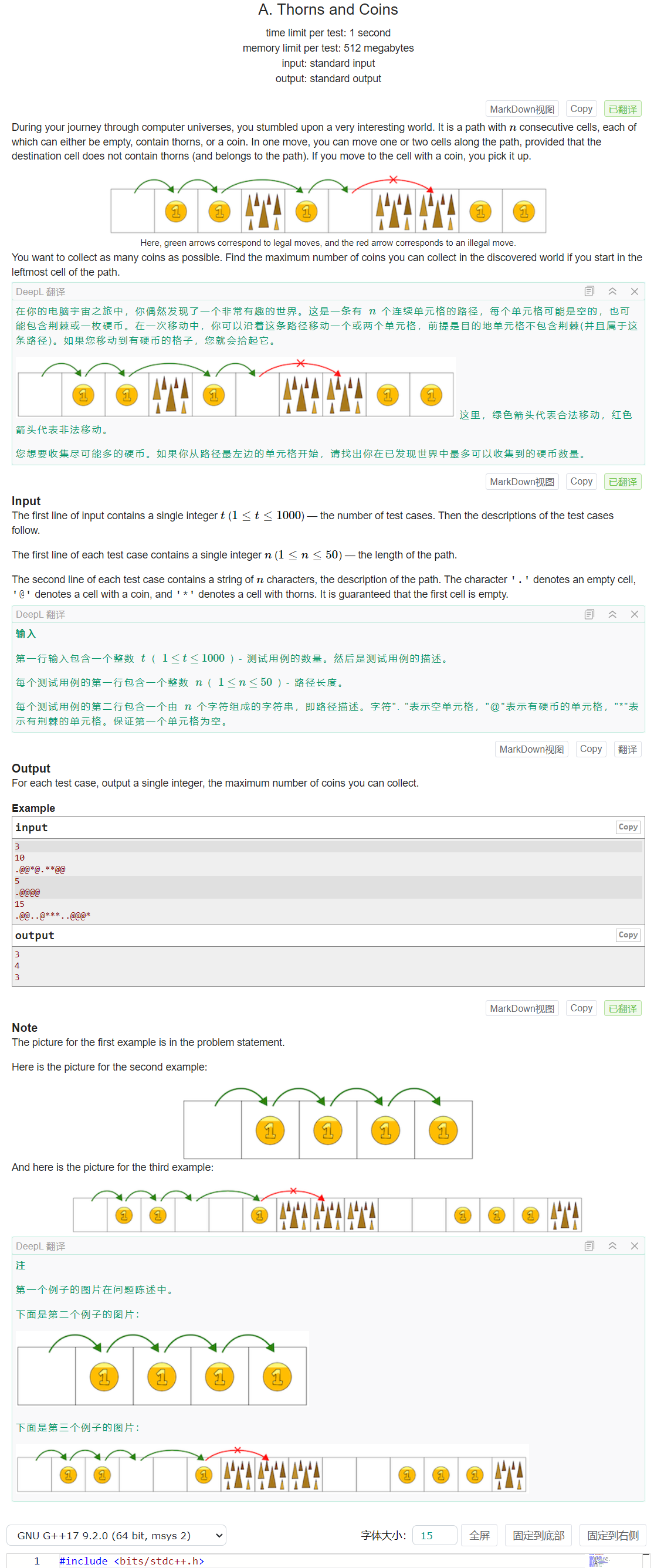
根据题意每一步只能走一步或者两步,很显然如果有连续的两个荆棘就不能走了,在不能走之前是一定可以把路上的金币全捡起来所以只需要边捡金币边判断是否能继续走下即可。
#include <bits/stdc++.h>
using ll = long long;
typedef std::pair<int, int> PII;
typedef std::array<ll, 3> ay;
const int N = 3e5 + 10, M = N << 1;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f;
const int MOD = 1e9 + 7;
#define ls u << 1
#define rs u << 1 | 1
int n, m;
inline void solve() {
std::cin >> n;
std::string str;
std::cin >> str;
int ans = 0;
for (int i = 0; i < n; i ++) {
if (str[i] == '@') ans ++;
else if (str[i] == '*' && i + 1 < n && str[i + 1] == '*') break;
}
std::cout << ans << '\n';
}
signed main(void) {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int _ = 1;
std::cin >> _;
while (_ --) solve();
return 0;
}
B
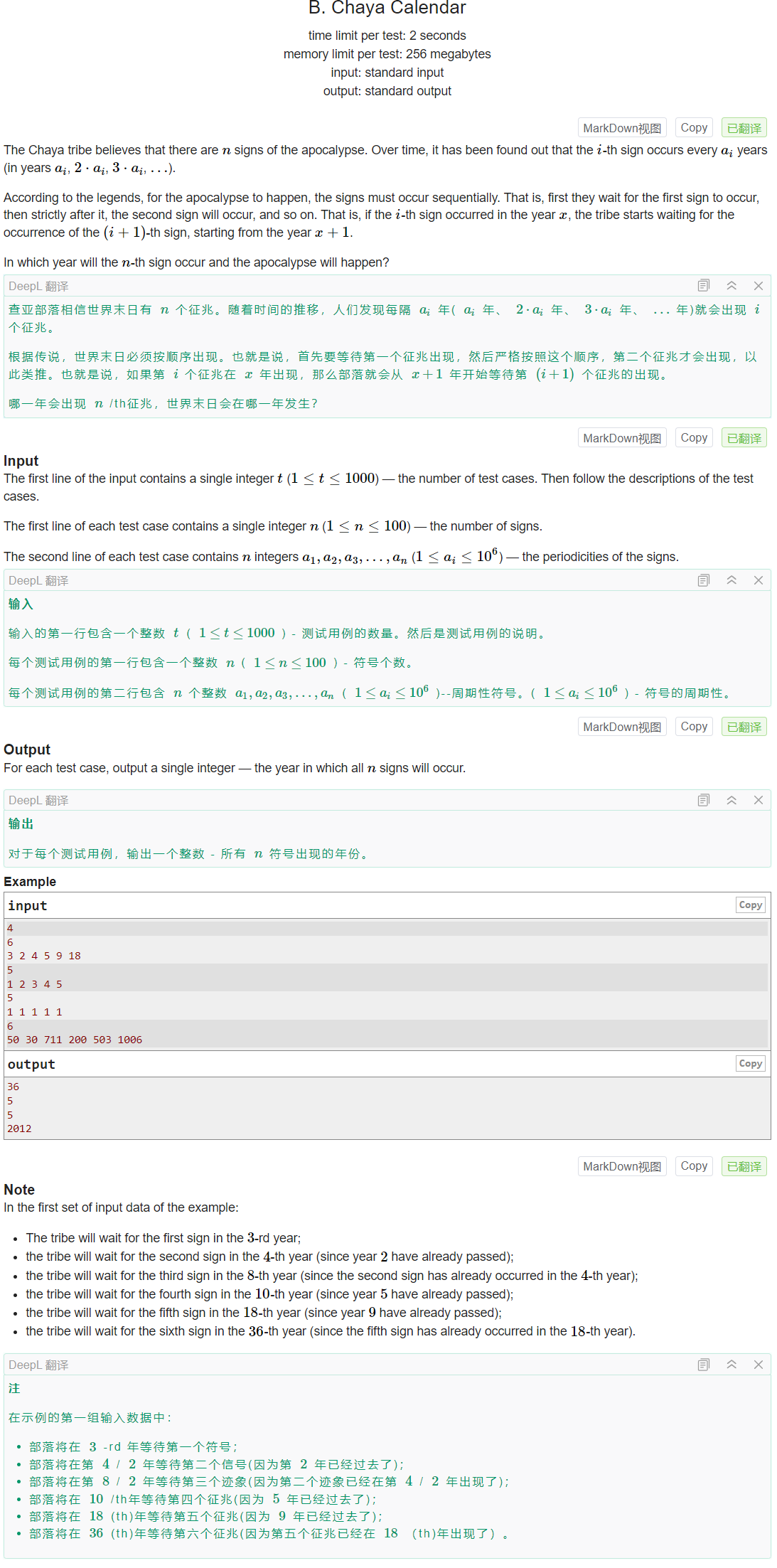
大致题意:给一个数组a,对于每个a[i]都可以被a[i]的任意整数倍替换,要求a数组每个元素变成从小到大的数组并且a[n]最小,最后后输出a[n]。
根据题意直接从模拟即可,从第二个元素开始让每个元素严格大于前一个元素。
#include <bits/stdc++.h>
using ll = long long;
typedef std::pair<int, int> PII;
typedef std::array<ll, 3> ay;
const int N = 3e5 + 10, M = N << 1;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f;
const int MOD = 1e9 + 7;
#define ls u << 1
#define rs u << 1 | 1
int n, m;
int a[N];
inline void solve() {
std::cin >> n;
for (int i = 1; i <= n; i ++) {
std::cin >> a[i];
if (i > 1) {
if (a[i] <= a[i - 1]) a[i] = (a[i - 1] / a[i] + 1) * a[i];
}
}
std::cout << a[n] << '\n';
}
signed main(void) {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int _ = 1;
std::cin >> _;
while (_ --) solve();
return 0;
}
C
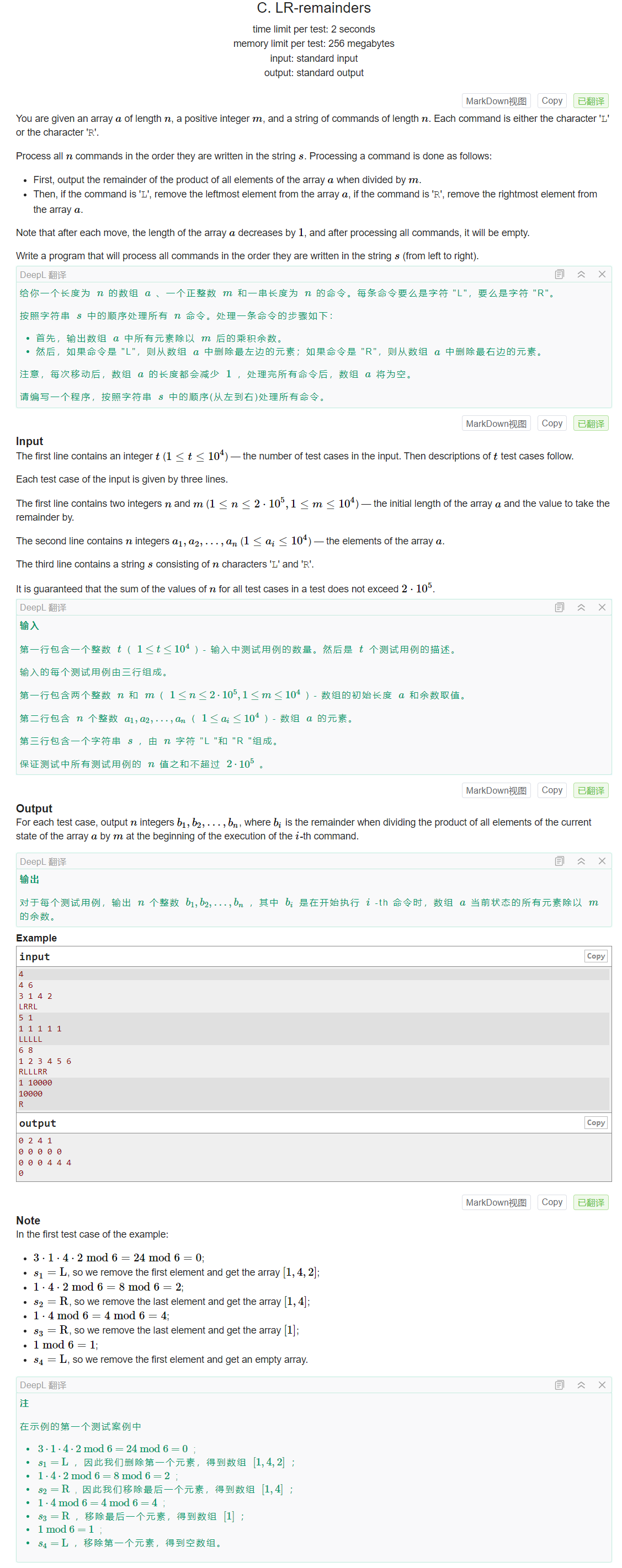
发现按照题意直接去写是一个超时的做法,但是倒着做就会变得非常正确,先找出最后一个被删除的位置pos,然后倒着模拟一遍即可。
#include <bits/stdc++.h>
using ll = long long;
typedef std::pair<int, int> PII;
typedef std::array<ll, 3> ay;
const int N = 3e5 + 10, M = N << 1;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f;
const int MOD = 1e9 + 7;
#define ls u << 1
#define rs u << 1 | 1
int n, m;
int a[N];
inline void solve() {
std::cin >> n >> m;
for (int i = 1; i <= n; i ++) {
std::cin >> a[i];
a[i] %= m;
}
std::vector<char> op;
int pos = 0;
for (int i = 1; i <= n; i ++) {
char ch;
std::cin >> ch;
op.push_back(ch);
if (ch == 'L') pos ++;
if (i == n && ch == 'R') pos ++;
}
std::reverse(op.begin(), op.end());
std::vector<int> ans;
int l = pos, r = pos;
for (int i = 0; i < op.size(); i ++) {
if (!i) ans.push_back(a[pos]);
else {
if (op[i] == 'L') {
l --;
ans.push_back(ans[i - 1] * a[l] % m);
}
else {
r ++;
ans.push_back(ans[i - 1] * a[r] % m);
}
}
}
for (int i = ans.size() - 1; ~i; i --) std::cout << ans[i] << ' ';
std::cout << '\n';
}
signed main(void) {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int _ = 1;
std::cin >> _;
while (_ --) solve();
return 0;
}
D
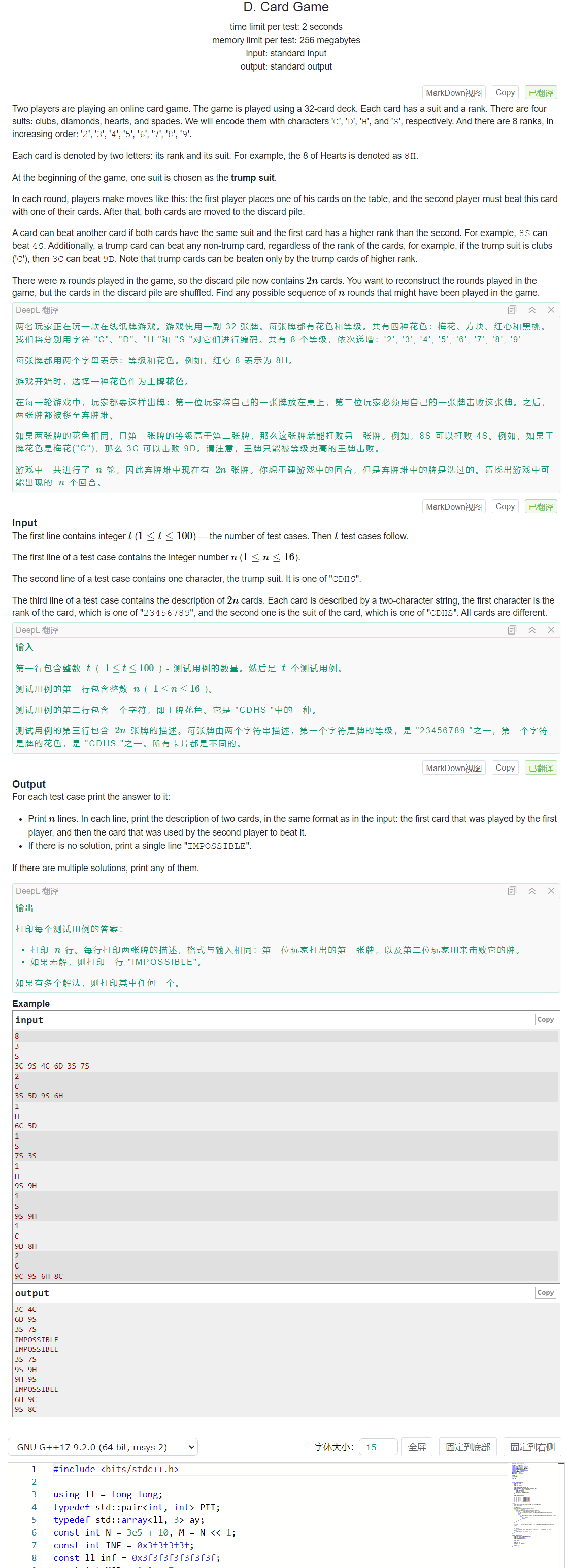
理解完题意发现除了王牌以外其他不同花色之间是不能分出胜负的,所以将输入数据按照花色分类并排序,让除了王牌以外的花色尽可能战胜相同花色,如果有这个花色数量为奇数那么最后会剩余一张就在王牌里挑一张战胜它即可。如果模拟过程中发现王牌不够用则无解。
#include <bits/stdc++.h>
using ll = long long;
typedef std::pair<int, int> PII;
typedef std::array<ll, 3> ay;
const int N = 3e5 + 10, M = N << 1;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f;
const int MOD = 1e9 + 7;
#define ls u << 1
#define rs u << 1 | 1
int n, m;
char ch;
inline void solve() {
std::cin >> n;
n *= 2;
std::cin >> ch;
std::vector<std::string> op;
std::map<char, std::vector<std::string>> mp;
for (int i = 1; i <= n; i ++) {
std::string str;
std::cin >> str;
mp[str[1]].push_back(str);
}
std::vector<char> s;
if (ch != 'C') s.push_back('C');
if (ch != 'D') s.push_back('D');
if (ch != 'H') s.push_back('H');
if (ch != 'S') s.push_back('S');
std::vector<std::pair<std::string, std::string>> ans;
bool ok = true;
int pos = 0;
std::sort(mp[ch].begin(), mp[ch].end());
for (int i = 0; i < 3; i ++) {
std::sort(mp[s[i]].begin(), mp[s[i]].end());
for (int j = 0; j < mp[s[i]].size(); j += 2) {
if (j + 1 < mp[s[i]].size()) ans.push_back({mp[s[i]][j], mp[s[i]][j + 1]});
else {
if (pos < mp[ch].size()) ans.push_back({mp[s[i]][j], mp[ch][pos ++]});
else {
ok = false;
break;
}
}
}
}
for (int i = pos; i < mp[ch].size(); i += 2) ans.push_back({mp[ch][i], mp[ch][i + 1]});
if (ok) {
for (auto x: ans) std::cout << x.first << ' ' << x.second << '\n';
} else {
std::cout << "IMPOSSIBLE" << '\n';
}
}
signed main(void) {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int _ = 1;
std::cin >> _;
while (_ --) solve();
return 0;
}
E
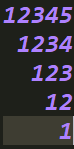
用字符串str表示输入的数字(处理完前导零)。对于个位而言改变的的次数是这个数字的大小,对于十位数字而言改变的次数就是这个str/10的以此类推。但是发现如果直接让str + str / 10 + ...这样是会超时。观察发现个位会被除了个位所有位置的数字都加上一遍,十位数会被除了个位和十位以外的数字都加上一遍。所以用前缀和的方式进行模拟即可,过程用数组模拟加法最后输出答案即可。
下图为12345数字的计算答案的加法表达式。(竖着看就是前缀和)
#include <bits/stdc++.h>
using ll = long long;
typedef std::pair<int, int> PII;
typedef std::array<ll, 3> ay;
const int N = 3e5 + 10, M = N << 1;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f;
const int MOD = 1e9 + 7;
#define ls u << 1
#define rs u << 1 | 1
int n, m;
int a[N];
char ch;
inline void solve() {
std::cin >> n;
std::string str, pt;
std::cin >> pt;
for (int i = 0; i < n; i ++)
if (pt[i] != '0') {
for (int j = i; j < n; j ++) str += pt[j];
break;
}
std::reverse(str.begin(), str.end());
n = str.length();
std::vector<int> count(str.length() * 2, 0), sum(str.length(), 0);
for (int i = 0; i < str.length(); i ++) {
sum[i] = str[i] - '0';
count[i] = str[i] - '0';
}
for (int i = n - 2; i >= 0; i --) sum[i] += sum[i + 1];
for (int i = 1; i < n; i ++) count[i - 1] += sum[i];
for (int i = 0; i < n * 2 - 1; i ++) {
count[i + 1] += count[i] / 10;
count[i] %= 10;
}
for (int i = n * 2 - 1; i >= 0; i --) {
if (count[i]) {
for (int j = i; ~j; j --) std::cout << count[j];
std::cout << '\n';
break;
}
}
}
signed main(void) {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int _ = 1;
std::cin >> _;
while (_ --) solve();
return 0;
}
F
1.线段树版本
抽象一下题意就是给定一个数轴然后给出m个线段,然后用一些钉子钉在线段上,每个线段上最多只能有一个钉子,要求被钉的线段尽可能的多。
因为数轴长度和不超过1e6,所以考虑从左往右枚举每个位置上有钉子的时候最优答案是多少,答案很显然就是当前位置被线段覆盖的次数加上左边所有合法钉子钉上的最多线段数量。边做边取最大值输出即可。
对于左边合法钉子的数量求之前需要知道当前覆盖当前位置的所有线段里面左端点最靠左的位置在哪里,这个可以用线段树的区间修改解决,求最大值可以用线段树的区间求最大值解决,两个线段树即可模拟完这个问题。区间覆盖的次数用差分前缀和解决即可。
#include <bits/stdc++.h>
using ll = long long;
typedef std::pair<int, int> PII;
typedef std::array<ll, 3> ay;
const int N = 1e6 + 10, M = N << 1;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f;
const int MOD = 1e9 + 7;
#define ls u << 1
#define rs u << 1 | 1
int n, m;
int a[N];
int mx[N << 2];
int left[N << 2];
inline void pushup(int u) {
mx[u] = std::max(mx[ls], mx[rs]);
}
inline void modify(int u, int L, int R, int x, int v) {
if (L == R) {
mx[u] = v;
return ;
}
int mid = L + R >> 1;
if (x <= mid) modify(ls, L, mid, x, v);
else modify(rs, mid + 1, R, x, v);
pushup(u);
}
inline int query(int u, int L, int R, int r) {
if (R <= r) return mx[u];
int mid = L + R >> 1;
int mx = query(ls, L, mid, r);
if (r > mid) mx = std::max(mx, query(rs, mid + 1, R, r));
return mx;
}
inline void pushdown(int u) {
if (left[u] != INF) {
left[ls] = std::min(left[ls], left[u]);
left[rs] = std::min(left[rs], left[u]);
left[u] = INF;
}
}
inline void build(int u, int L, int R) {
left[u] = INF;
if (L == R) return;
int mid = L + R >> 1;
build(ls, L, mid);
build(rs, mid + 1, R);
}
inline void modify(int u, int L, int R, int l, int r, int mn) {
if (L >= l && R <= r) {
left[u] = std::min(left[u], mn);
return ;
}
pushdown(u);
int mid = L + R >> 1;
if (l <= mid) modify(ls, L, mid, l, r, mn);
if (r > mid) modify(rs, mid + 1, R, l, r, mn);
}
inline int queryl(int u, int L, int R, int x) {
if (L == R) return left[u];
int mid = L + R >> 1;
pushdown(u);
if (x <= mid) return queryl(ls, L, mid, x);
return queryl(rs, mid + 1, R, x);
}
inline void solve() {
std::cin >> n >> m;
build(1, 1, n);
std::vector<int> sum(n + 2);
for (int i = 1; i <= m; i ++) {
int l, r;
std::cin >> l >> r;
sum[l] ++;
sum[r + 1] --;
modify(1, 1, n, l, r, l);
}
for (int i = 1; i <= n; i ++) sum[i] += sum[i - 1];
std::vector<int> dp(n + 1, 0);
int ans = 0;
for (int i = 1; i <= n; i ++) {
int now = 0;
if (i == 1) now = sum[1];
else {
int pos = queryl(1, 1, n, i);
if (pos == 1) now = sum[i];
else if (pos != INF) now = query(1, 1, n, pos - 1) + sum[i];
}
modify(1, 1, n, i, now);
ans = std::max(ans, now);
}
std::cout << ans << '\n';
}
signed main(void) {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int _ = 1;
std::cin >> _;
while (_ --) solve();
return 0;
}
2.排序 + Multiset + 前缀和 + dp版本
抽象一下题意就是给定一个数轴然后给出m个线段,然后用一些钉子钉在线段上,每个线段上最多只能有一个钉子,要求被钉的线段尽可能的多。
从左往右枚举每个位置被钉上钉子的时候当前位置的最优答案是多少,答案显然是当前点被线段覆盖的次数加上左边其他合法钉子的钉上线段的最大值。
对于每个点被线段覆盖的次数可以用差分加前缀和维护。用dp数组表示到当前位置为止合法的最大值是多少。需要维护覆盖每个位置的线段左端点最小值才可以知道左边合法钉子的位置。从左往右扫描整个数轴,碰到左端点添加进multiset,到了右端点就从multiset删除,这样对于每个位置最左边的端点就是begin();答案就是当前位置被覆盖的数量加上dp[*begin() - 1]。
#include <bits/stdc++.h>
using ll = long long;
typedef std::pair<int, int> PII;
typedef std::array<ll, 3> ay;
const int N = 3e5 + 10, M = N << 1;
const int INF = 0x3f3f3f3f;
const ll inf = 0x3f3f3f3f3f3f3f;
const int MOD = 1e9 + 7;
#define ls u << 1
#define rs u << 1 | 1
int n, m;
int a[N];
inline void solve() {
std::cin >> n >> m;
std::vector<PII> seg;
std::vector<int> dp(n + 1), sum(n + 2);
std::vector<std::vector<int>> era(n + 1, std::vector<int>()), add(n + 1, std::vector<int>());
std::multiset<int> st;
for (int i = 1; i <= m; i ++) {
int x, y;
std::cin >> x >> y;
seg.push_back({x, y});
sum[x] ++, sum[y + 1] --;
era[y].push_back(x);
add[x].push_back(x);
}
std::sort(seg.begin(), seg.end());
for (int i = 1; i <= n; i ++) {
sum[i] += sum[i - 1];
for (int j = 0; j < add[i].size(); j ++)
st.insert(add[i][j]);
int left = 0;
if (st.size()) left = *st.begin();
if (left) dp[i] = std::max(dp[i - 1], sum[i] + dp[left - 1]);
else dp[i] = dp[i - 1];
for (int j = 0; j < era[i].size(); j ++)
st.erase(st.find(era[i][j]));
}
std::cout << dp[n] << '\n';
}
signed main(void) {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int _ = 1;
std::cin >> _;
while (_ --) solve();
return 0;
}
G
传送门
不会