Codeforces Round 406 (Div. 2) D. Legacy 线段树优化建图
题目大意:
给定n个点,m个操作,和起点s。其中n 和 q 大于等于1小于等于1e5, s大于等于1小于等于n
其中m个操作有三种情况:
1.输入1 u v val 表示从u号点向v号点连一个权值为val的有向边,其中1 <= u <= n, 1 <= v <= n, 1 <= val <= 1e9
2.输入2 u l r val 表示从u号点向区间[l, r]所有的点连一个权值为val的有向边,其中1 <= u <= n, 1 <= l <= r <= n, 1 <= val <= 1e9
3.输入3 u l r val 表示从区间[l, r]所有的点向u连一个权值为val的有向边,其中1 <= u <= n, 1 <= l <= r <= n, 1 <= val <= 1e9
最后求从起点s出发能到达所有点的最短距离,如果无法到达输出-1
解题思路:
区间问题可以联想到线段树。
看操作2如何处理,如果我们拥有一种这种类似于线段树的图形结构。假设n为8,我们让所叶子的编号都是从1-n,也就是让叶子代表1-n这些点。
如果我们如图所示连了边权为0的有向边,那么要表示从2号点向[3, 4]这个区间连了权值为5的有向边就可以表示为2到12号点连了边权为5的有向边。因为12号点向3和4号点连了边权为0的有向边也就是说12号点可以到达3和4号点,那么如果3号向区间[5, 6]也就是编号14的点的连了条边权为6的有向边,如果我们从2号点出发能否求出到达5, 6号点的最短路呢?很显然是可以的,2会达到12号点,那么到达12号点的最短路为5,12号点能到达3号点,于是可以算出到达3号点的最短路为5,3号点能到达14号点,所以到达14号点的最短路为11,14号点能到达5, 6号点且边权为0,所以到达5, 6号点的最短路为11。

接下来看操作三如何处理,还是假设n为8的情况。我们有这样一个图,分析方法和操作2一样可以自己试试。
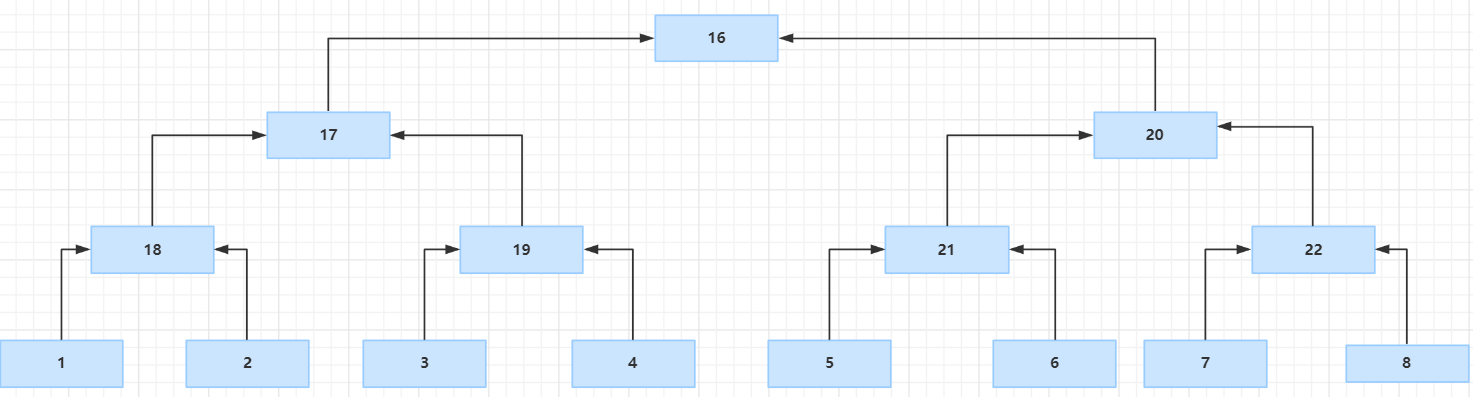
也就是说我们建出这样的图,再根据题目要求连边跑一遍最短路就可以解出答案了。
#include <bits/stdc++.h>
using ll = long long;
using ld = long double;
const int N = 8e5 + 10, M = N << 1;
const ll INF = 0x3f3f3f3f3f3f3f3f;
typedef std::pair<ll, int> PII;
typedef std::array<int, 3> ay;
#define ls tr[u].l
#define rs tr[u].r
struct node {
int l, r;
}tr[N];
int idx, id;
int h[N << 1], ne[N << 2], e[N << 2], w[N << 2];
ll dis[N];
bool vis[N];
int n, m, s, rt1, rt2;
inline void add(int a, int b, int c) {
ne[idx] = h[a], e[idx] = b, w[idx] = c, h[a] = idx ++;
}
inline void buildOut(int &u, int L, int R) {
if (L == R) {
u = L;
return ;
}
u = ++ id;
int mid = L + R >> 1;
buildOut(ls, L, mid);
buildOut(rs, mid + 1, R);
add(u, ls, 0);
add(u, rs, 0);
}
inline void buildIn(int &u, int L, int R) {
if (L == R) {
u = L;
return ;
}
u = ++ id;
int mid = L + R >> 1;
buildIn(ls, L, mid);
buildIn(rs, mid + 1, R);
add(ls, u, 0);
add(rs, u, 0);
}
inline void update(int u, int L, int R, int v, int l, int r, int type, int val) {
if (L >= l && R <= r) {
if (type == 2) add(v, u, val);
else add(u, v, val);
return ;
}
int mid = L + R >> 1;
if (l <= mid) update(ls, L, mid, v, l, r, type, val);
if (r > mid) update(rs, mid + 1, R, v, l, r, type, val);
}
inline void Dijkstra() {
std::priority_queue<PII, std::vector<PII>, std::greater<PII>> q;
memset(dis, 0x3f, sizeof dis);
memset(vis, false, sizeof vis);
dis[s] = 0;
q.push({0, s});
while (!q.empty()) {
int u = q.top().second;
int VAL = q.top().first;
q.pop();
if (vis[u]) continue;
vis[u] = true;
for (int i = h[u]; ~i; i = ne[i]) {
int j = e[i], val = w[i];
if (dis[u] + val < dis[j]) {
dis[j] = dis[u] + val;
q.push({dis[j], j});
}
}
}
}
std::string str;
inline void solve() {
memset(h, -1, sizeof h);
std::cin >> n >> m >> s;
id = n;
buildOut(rt1, 1, n), buildIn(rt2, 1, n);
while (m --) {
int op, u, l, r, val;
std::cin >> op >> u >> l;
if (op == 1) {
std::cin >> val;
add(u, l, val);
} else if (op == 2) {
std::cin >> r >> val;
update(rt1, 1, n, u, l, r, 2, val);
} else {
std::cin >> r >> val;
update(rt2, 1, n, u, l, r, 3, val);
}
}
Dijkstra();
for (int i = 1; i <= n; i ++) {
if (dis[i] != INF)
std::cout << dis[i] << ' ';
else std::cout << -1 << ' ';
}
}
signed main(void) {
std::ios::sync_with_stdio(false);
std::cin.tie(nullptr);
std::cout.tie(nullptr);
int _ = 1;
while (_ --) solve();
return 0;
}

