河南省第十三届ICPC大学生程序设计竞赛 G.Elo mountains （可持久化数组 + AC自动机）

传送门

解题思路:

  首先考虑如果字符集大小不是1e5的写法：如果字符集大小为26，我们首先对于这整棵树求出子树大小，然后构建出AC自动机的fail指针，我们会发现每个点的答案就是fail指针上所有结点的子树大小，下面是原树。

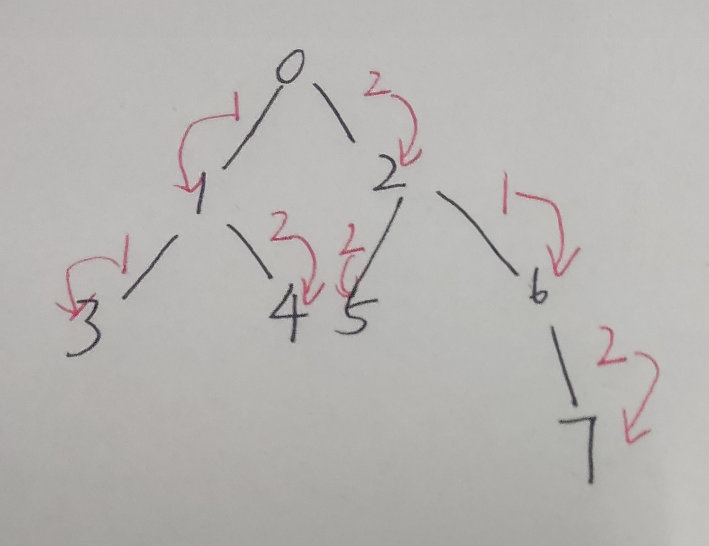
  我们可以把边权转化为点权来理解，也就是把每条边父亲与儿子的连边的权值赋给儿子。我们不难发现对于0->1而言子串为1，我们需要在整颗子树里面查找1出现的次数。答案就是1号点的子树大小加上3号点的子树大小加上6号点的子树大小，答案也就是3 + 1 + 2 = 6。然后对于0->1而言子串为12，我们需要在整颗子树里面查找以12为结尾的子树大小也就是4号点的子树大小以及7号点的子树大小，答案也就是2。因为对于任何一条路径如果如果到父亲出现了想要的子串那么到儿子一定也会出现。现在问题就变成了如何对于一个子串我们如何去找出他的所有终止节点的所有子树大小。AC自动机是可以做这个事情的。如下图为样例的fail树。

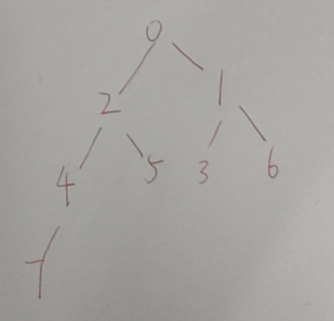
  我们会发现对于这颗fail树而言，儿子的答案都会贡献给父亲，因为父亲是儿子的前缀，我们利用这个性质把每个子树的答案用加到父亲上就能得到答案。对于叶子3,6,5,7而言答案为原树的子树大小1,2,1,1。4的子树大小为4本身加上7的子树大小，所以4的答案为2，一次类推2的答案为7,1的答案为6。

  但是这题的字符集大小为100000如果直接构建ac自动机我们总不能开一个100000 * 100000大小的数组吧。如果使用map的话给我们一个4e5长度的链，再给一个菊花插到尾部我们fail指针往上跳的时间复杂度就高的吓人。所以考虑用可持久化数组优化AC自动机的构造即可，这样的话就可以在log的时间复杂度内跳转到有效的fail指针。

摸鱼ing

#include <bits/stdc++.h>

int n, m;

const int N = 1e5 + 10;
typedef std::pair<int, int> PII;
std::map<int, int> tr[N];
int h[N], ne[N << 1], e[N << 1], w[N << 1], idx, sz[N];

inline void add(int a, int b, int c) {
	ne[idx] = h[a], e[idx] = b, w[idx] = c, h[a] = idx ++;
}

inline void add(int a, int b) {
	ne[idx] = h[a], e[idx] = b, h[a] = idx ++;
}

int val[N << 5], root[N << 5], tot, l[N << 5], r[N << 5], nxt[N << 5];
int dfn[N], timedelta, id[N];

inline void insert(int &u, int L, int R, int x, int v) {
	int last = u;
	u = ++ tot;
	if (L == R) {
		val[u] = v;
		return ;	
	}
	l[u] = l[last];
	r[u] = r[last];
	int mid = L + R >> 1;
	if (x <= mid) insert(l[u], L, mid, x, v);
	else insert(r[u], mid + 1, R, x, v);
}

inline int query(int u, int L, int R, int x) {
	if (L == R) return val[u];
	
	int mid = L + R >> 1;
	if (x <= mid)	return query(l[u], L, mid, x);
	return query(r[u], mid + 1, R, x);
}

inline void solve() {
	std::cin >> n;
	
	memset(h, -1, sizeof h);
	for (int i = 0; i < n; i ++) {
		int a, b, c;
		std::cin >> a >> b >> c;
		add(a, b, c);
		add(b, a, c);
	}
	
	{
		std::function<void(int, int)> dfs = [&](int u, int fa) -> void{
			sz[u] = 1;
			for (int i = h[u]; ~i; i = ne[i]) {
				int j = e[i], v = w[i];
				if (j == fa)	continue;
				tr[u][j] = v;
				dfs(j, u);
				sz[u] += sz[j];
			}
		};
		dfs(0, -1);
	}
	
	
	{
		int p = 0;
		std::queue<int> q;
		for (auto &[x, v]: tr[p]) {
			q.push(x);
			nxt[v] = 0;
			insert(root[p], 1, 1e5, v, x);
		}
			
		while (!q.empty()) {
			int tq = q.front();
			q.pop();
			root[tq] = root[nxt[tq]];
			for(auto &[x, v]: tr[tq]){
				int t = query(root[tq], 1, 1e5, v);
				nxt[x] = t;
				insert(root[tq], 1, 1e5, v, x);	
				q.push(x);
			}
		}
	}
	
	memset(h, -1, sizeof h);
	idx = 0;
	
	{
		std::vector<long long> dp(n + 1);
		for (int i = 1; i <= n; i ++) {
			dp[nxt[i]] += sz[i];
			add(nxt[i], i);
		}
		
		std::function<void(int)> dfs = [&](int u) -> void{
			for (int i = h[u]; ~i; i = ne[i]) {
				int j = e[i];
				dfs(j);
				dp[u] += dp[j];
			}
		};
		dfs(0);
		
		for (int i = 1; i <= n; i ++) dp[i] += sz[i];
		for (int i = 1; i <= n; i ++)	std::cout << dp[i] << '\n';
	}
}

int main(void) {
	std::ios::sync_with_stdio(false);
	std::cin.tie(nullptr);
	std::cout.tie(nullptr);
	
	int _ = 1;
	//std::cin >> _;
	
	while (_ --) solve();
	
	return 0;
}