2023年中国高校计算机大赛-团队程序设计天梯赛(GPLT)上海理工大学校内选拔赛 L 捡贝壳 && 你能回答这些问题吗
一道类似捡贝壳的简化版本,这个题写了再写捡贝壳比较好
你能回答这些问题吗
很明显这种区间问题会用到线段树,然后首先考虑如何维护区间最大连续子序列,我们会发现对于线段树上每个非叶子结点(有儿子的结点)最大子序列无非就三种可能,一种是被左儿子完全覆盖,另一种是被右儿子完全覆盖,最后一种就是左儿子从左儿子的最右边往左走的的最大值(rmx)加上右儿子从右儿子的最左边往右走的最大值(lmx)。那么如何维护左右儿子的rmx和lmx还有左右儿子的最大连续子序列值(mx)呢?
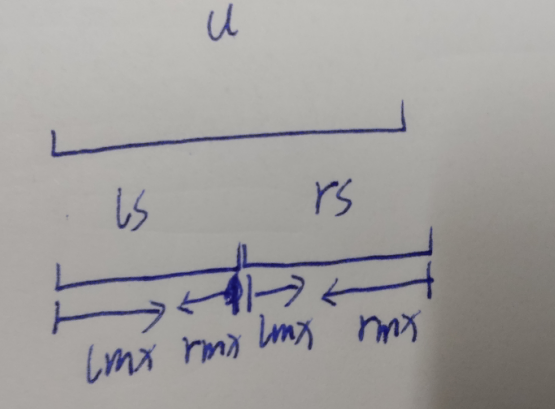
我们会发现在维护当前结点的lmx和rmx的时候有两个可能,当前节点的lmx的一个可能是左子树的lmx,另一个可能是左子树的总和加上右子树的lmx,我们需要取最大值。当前节点的rmx同理,这么一来我就需要再维护一个区间累加和。
我们线段树上维护四个信息,从左端点向右连续的最大值lmx,从右端点向左连续的最大值rmx,区间最大值mx,区间和sum,在叶子结点的时候rmx=lmx=mx=sum=叶子对应的值,每次pushup的时候如何维护四个信息?
对于lmx更新的时候需要用左儿子的lmx和左儿子的和加上右儿子的lmx取max
对于rmx更新的时候需要用右儿子的rmx和右儿子的和加上左儿子的rmx取max
对于sum直接左右儿子加起来即可
对于区间最值,在左儿子的mx和右儿子的mx和左儿子的rmx加上右儿子的lmx取max即可
代码实现如下
#include <iostream>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <stack>
#include <queue>
#include <numeric>
#include <cassert>
#include <bitset>
#include <cstdio>
#include <vector>
#include <unordered_set>
#include <cmath>
#include <map>
#include <unordered_map>
#include <set>
#include <deque>
#include <tuple>
#include <array>
#define all(a) a.begin(), a.end()
#define cnt0(x) __builtin_ctz(x)
#define endl '\n'
#define ll long long
#define ull unsigned long long
#define cntone(x) __builtin_popcount(x)
#define db double
#define fs first
#define se second
#define AC main(void)
#define HYS std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);
typedef std::pair<int, int > PII;
typedef std::pair<int, std::pair<int, int>> PIII;
typedef std::pair<ll, ll> Pll;
typedef std::pair<double, double> PDD;
using ld = double long;
const long double eps = 1e-9;
const int INF = 0x3f3f3f3f;
const int N = 5e5 + 10, M = 4e5 + 10;
int n , m, p;
int d1[] = {0, 0, 1, -1};
int d2[] = {1, -1, 0, 0};
int a[N];
struct node{
int l, r;
ll lmx, rmx, sum, mx;
}tr[N << 2];
inline void pushup(node &u,node &l,node &r){
u.sum = l.sum + r.sum;
u.lmx = std::max(l.lmx, l.sum + r.lmx);
u.rmx = std::max(r.rmx, r.sum + l.rmx);
u.mx = std::max({l.mx, r.mx, l.rmx + r.lmx});
}
inline void pushup(int u){
pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}
inline void build_tree(int u, int l, int r){
tr[u] = {l, r};
if(l == r){
tr[u].lmx = tr[u].rmx = tr[u].mx = tr[u].sum = a[l];
return ;
}
int mid = l + r >> 1;
build_tree(u << 1, l, mid);
build_tree(u << 1 | 1, mid + 1, r);
pushup(u);
}
inline void modify(int u, int x, int v){
if(tr[u].l == tr[u].r){
tr[u].sum = tr[u].lmx = tr[u].rmx = tr[u].mx = v;
return ;
}
int mid = tr[u].l + tr[u].r >> 1;
if(x <= mid) modify(u << 1, x, v);
else modify(u << 1 | 1, x, v);
pushup(u);
}
inline node query(int u, int l, int r){
if(tr[u].l >= l && tr[u].r <= r) return tr[u];
int mid = tr[u].l + tr[u].r >> 1;
if(r <= mid) return query(u << 1, l, r);
if(l > mid) return query(u << 1 | 1, l ,r);
node res;
node ls = query(u << 1, l, r);
node rs = query(u << 1 | 1, l, r);
pushup(res, ls, rs);
return res;
}
inline void solve(){
std::cin >> n >> m;
for(int i = 1; i <= n; i ++) std::cin >> a[i];
build_tree(1, 1, n);
while(m --){
int op, l, r;
std::cin >> op >> l >> r;
if(op == 1){
if(l > r) std::swap(l, r);
std::cout << query(1, l, r).mx << '\n';
}
else modify(1, l, r);
}
}
signed AC{
HYS
int _ = 1;
//std::cin >> _;
while(_ --)
solve();
return 0;
}
取贝壳
这题思路和上题类似,只不过我们需要把维护一个lmx,rmx,mx,sum变成维护16个lmx,rmx,mx和一个区间长度。lazy是懒标记下传,state每个结点里面有哪些贝壳。
因为最多有四种贝壳,所以我们可以考虑状态压缩把四种贝壳表示为1——15之间的整数,然后区间状态合并变成区间或。
因为n是3e5所以进行pushup的时候用两个for循环枚举所有状态进行暴力转移即可。
需要注意的细节
用i枚举左儿子状态和j枚举右儿子状态的时候,如果i与上左儿子的state不等于i的话就说明当前的i这个状态是不能被左儿子完全包含的所以就不能用左儿子的len+右儿子的lmx来更新当前节点的lmx,当前结点的rmx也同理。
#include <iostream>
#include <cstring>
#include <iomanip>
#include <algorithm>
#include <stack>
#include <queue>
#include <numeric>
#include <cassert>
#include <bitset>
#include <cstdio>
#include <vector>
#include <unordered_set>
#include <cmath>
#include <map>
#include <unordered_map>
#include <set>
#include <deque>
#include <tuple>
#include <array>
#define all(a) a.begin(), a.end()
#define cnt0(x) __builtin_ctz(x)
#define endl '\n'
#define ll long long
#define ull unsigned long long
#define cntone(x) __builtin_popcount(x)
#define db double
#define fs first
#define se second
#define AC main(void)
#define HYS std::ios::sync_with_stdio(false);std::cin.tie(0);std::cout.tie(0);
typedef std::pair<int, int > PII;
typedef std::pair<int, std::pair<int, int>> PIII;
typedef std::pair<ll, ll> Pll;
typedef std::pair<double, double> PDD;
using ld = double long;
const long double eps = 1e-9;
const int INF = 0x3f3f3f3f;
const int N = 2e5 + 10, M = 4e5 + 10;
int n , m, p;
int d1[] = {0, 0, 1, -1};
int d2[] = {1, -1, 0, 0};
int a[N];
struct node{
int l, r;
int state, lazy;
int lmn[16], rmn[16], mn[16], len;
}tr[N << 2];
int target = 15;
inline void pushup(node &u,node &ls,node &rs){
u.len = ls.len + rs.len;
u.state = ls.state | rs.state;
for(int i = 1; i < 16; i ++){
u.lmn[i] = ls.lmn[i];
u.rmn[i] = rs.rmn[i];
u.mn[i] = std::min(ls.mn[i], rs.mn[i]);
}
for(int i = 1; i < 16; i ++){
for(int j = 1; j < 16; j ++){
int tmp = i | j;
if((ls.state & i) == i) u.lmn[tmp] = std::min(u.lmn[tmp], ls.len + rs.lmn[j]);
if((rs.state & j) == j) u.rmn[tmp] = std::min(u.rmn[tmp], rs.len + ls.rmn[i]);
u.mn[tmp] = std::min({u.mn[tmp], ls.rmn[i] + rs.lmn[j]});
}
}
}
inline void pushup(int u){
pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}
inline void Do(int u, int v){
memset(tr[u].lmn, 0x3f, sizeof tr[u].lmn);
memset(tr[u].rmn, 0x3f, sizeof tr[u].rmn);
memset(tr[u].mn, 0x3f, sizeof tr[u].mn);
tr[u].state = v;
tr[u].lmn[v] = tr[u].mn[v] = tr[u].rmn[v] = 1;
tr[u].lazy = v;
}
inline void pushdown(int u){
if(tr[u].lazy){
Do(u << 1, tr[u].lazy);
Do(u << 1 | 1, tr[u].lazy);
tr[u].lazy = 0;
}
}
inline void build_tree(int u, int l, int r){
tr[u] = {l, r};
if(l == r){
int t = 1 << (a[l] - 1);
tr[u].state = t;
memset(tr[u].lmn, 0x3f, sizeof tr[u].lmn);
memset(tr[u].rmn, 0x3f, sizeof tr[u].rmn);
memset(tr[u].mn, 0x3f, sizeof tr[u].mn);
tr[u].lmn[t] = tr[u].rmn[t] = tr[u].len = tr[u].mn[t] = 1;
return ;
}
int mid = l + r >> 1;
build_tree(u << 1, l, mid);
build_tree(u << 1 | 1, mid + 1, r);
pushup(u);
}
inline void modify(int u, int l, int r, int v){
if(tr[u].l >= l && tr[u].r <= r){
Do(u, v);
return ;
}
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
if(l <= mid) modify(u << 1, l, r, v);
if(r > mid) modify(u << 1 | 1, l, r, v);
pushup(u);
}
inline node query(int u, int l, int r){
if(tr[u].l >= l && tr[u].r <= r) return tr[u];
pushdown(u);
int mid = tr[u].l + tr[u].r >> 1;
if(r <= mid) return query(u << 1, l, r);
if(l > mid) return query(u << 1 | 1, l, r);
node res;
node ls = query(u << 1, l, r);
node rs = query(u << 1 | 1, l, r);
pushup(res, ls, rs);
pushup(u);
return res;
}
inline void solve(){
std::cin >> n;
for(int i = 1; i <= n; i ++) std::cin >> a[i];
build_tree(1, 1, n);
std::cin >> m;
for(int i = 1; i <= m; i ++){
int op, l, r, v;
std::cin >> op >> l >> r;
if(op == 1){
std::cin >> v;
v = 1 << (v - 1);
modify(1, l, r, v);
}
else{
int tmp = query(1, l, r).mn[15];
if(tmp != INF) std::cout << tmp << '\n';
else std::cout << -1 << '\n';
}
}
}
signed AC{
HYS
int _ = 1;
//std::cin >> _;
while(_ --)
solve();
return 0;
}

