第46届ICPC亚洲区域赛（昆明）(正式赛）B Blocks

题目链接

不会求概率，队友写的概率，他传给我一个二进制状态sta我只负责check一下是否合法
他推的公式如下

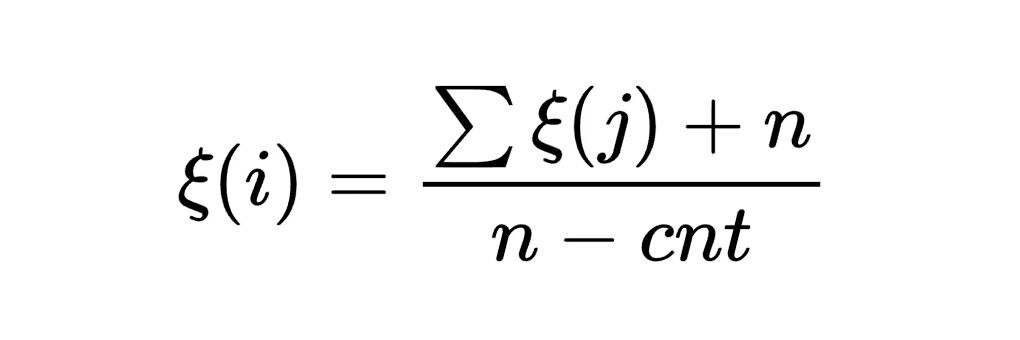
在这题进行线段树扫描线的时候遇到了之前没遇到的问题，如果l和r重合了那么是不需要进行modify的（105行），否则会RE，如果只有一个点构不成区间需要直接return false掉，否则RE。然后需要注意给点的可能会超过w和h所以记得取min。其他的部分也就是线段树扫描线的板子了。

#include <bits/stdc++.h>
using namespace std;
const int N = 11, M = 1e6 + 10;
const int MOD = 998244353;
template <unsigned M_> struct ModInt {
    static constexpr unsigned M = M_;
    unsigned x;
    constexpr ModInt() : x(0U) {}
    constexpr ModInt(unsigned x_) : x(x_ % M) {}
    constexpr ModInt(unsigned long long x_) : x(x_ % M) {}
    constexpr ModInt(int x_) : x(((x_ %= static_cast<int>(M)) < 0) ? (x_ + static_cast<int>(M)) : x_) {}
    constexpr ModInt(long long x_) : x(((x_ %= static_cast<long long>(M)) < 0) ? (x_ + static_cast<long long>(M)) : x_) {}
    ModInt &operator+=(const ModInt &a) { x = ((x += a.x) >= M) ? (x - M) : x; return *this; }
    ModInt &operator-=(const ModInt &a) { x = ((x -= a.x) >= M) ? (x + M) : x; return *this; }
    ModInt &operator*=(const ModInt &a) { x = (static_cast<unsigned long long>(x) * a.x) % M; return *this; }
    ModInt &operator/=(const ModInt &a) { return (*this *= a.inv()); }
    ModInt pow(long long e) const {
        if (e < 0) return inv().pow(-e);
        ModInt a = *this, b = 1U; for (; e; e >>= 1) { if (e & 1) b *= a; a *= a; } return b;
    }
    ModInt inv() const {
        unsigned a = M, b = x; int y = 0, z = 1;
        for (; b; ) { const unsigned q = a / b; const unsigned c = a - q * b; a = b; b = c; const int w = y - static_cast<int>(q) * z; y = z; z = w; }
        assert(a == 1U); return ModInt(y);
    }
    ModInt operator+() const { return *this; }
    ModInt operator-() const { ModInt a; a.x = x ? (M - x) : 0U; return a; }
    ModInt operator+(const ModInt &a) const { return (ModInt(*this) += a); }
    ModInt operator-(const ModInt &a) const { return (ModInt(*this) -= a); }
    ModInt operator*(const ModInt &a) const { return (ModInt(*this) *= a); }
    ModInt operator/(const ModInt &a) const { return (ModInt(*this) /= a); }
    template <class T> friend ModInt operator+(T a, const ModInt &b) { return (ModInt(a) += b); }
    template <class T> friend ModInt operator-(T a, const ModInt &b) { return (ModInt(a) -= b); }
    template <class T> friend ModInt operator*(T a, const ModInt &b) { return (ModInt(a) *= b); }
    template <class T> friend ModInt operator/(T a, const ModInt &b) { return (ModInt(a) /= b); }
    explicit operator bool() const { return x; }
    bool operator==(const ModInt &a) const { return (x == a.x); }
    bool operator!=(const ModInt &a) const { return (x != a.x); }
    friend std::ostream &operator<<(std::ostream &os, const ModInt &a) { return os << a.x; }
};
using Mint = ModInt<MOD>;
int TT, n, w, h, xa[N], ya[N], xb[N], yb[N];
int valid[1 << N], vis[1 << N];
Mint inv[N], f[1 << N];
int sz;

std::vector<int>	nums;

struct Segment{
	int x, y1, y2, k;
}seg[1000];

struct Node{
	int l, r;
	int len;
	int cnt;
}tr[1000];

inline void pushup(int u){
	if(tr[u].cnt)	tr[u].len = nums[tr[u].r + 1] - nums[tr[u].l];
	else if(tr[u].l != tr[u].r)	tr[u].len = tr[u << 1].len + tr[u << 1 | 1].len;
	else tr[u].len = 0;
}

inline void build_tree(int u, int l, int r){
	tr[u] = {l, r, 0, 0};
	if(l == r)	return ;
	int mid = l + r >> 1;
	build_tree(u << 1, l, mid);
	build_tree(u << 1 | 1, mid + 1, r);
}

inline void modify(int u, int l, int r, int k){
	if(tr[u].l >= l && tr[u].r <= r){
		tr[u].cnt += k;
		pushup(u);
		return ;
	}
	int mid = tr[u].l + tr[u].r >> 1;
	if(l <= mid)	modify(u << 1, l, r, k);
	if(r > mid)	modify(u << 1 | 1, l, r, k);
	pushup(u);
}

bool cmp(Segment a, Segment b){
	return a.x < b.x;
}

int check(int sta) {
	int p = 0;
	for(int i = 0; i < n; i ++){
		if((sta >> i) & 1){
			seg[p ++] = {xa[i], ya[i], yb[i], 1};
			seg[p ++] = {xb[i], ya[i], yb[i], -1};
		}
	}
	std::sort(seg, seg + p, cmp);
	if(sz < 0)	return 0 == w * h;
	build_tree(1, 0, sz);
	long long res = 0;
	for(int i = 0; i < p; i ++){
		if(i)	res += 1ll * tr[1].len * (seg[i].x - seg[i - 1].x);
		int l = lower_bound(nums.begin(), nums.end(), seg[i].y1) - nums.begin();
		int r = lower_bound(nums.begin(), nums.end(), seg[i].y2) - nums.begin() - 1;
		if(r < l)	continue;
		modify(1, l, r, seg[i].k);
	}
	return res == 1ll * w * h;
}

Mint dfs(int sta) {
    if (vis[sta]) return f[sta];
    if (valid[sta]) return 0;
    Mint &res = f[sta];
    int cnt = __builtin_popcount(sta);
    for (int i = 0; i < n; i++) {
        if (!(sta >> i & 1)) {
            res += dfs(sta | (1 << i)) * inv[n];
        }
    }
    res = (res + 1) * n * inv[n - cnt];
    vis[sta] = 1;
    return res;
}
void Solution() {

    cin >> n >> w >> h;
    nums.clear();
    for(int i = 0; i < (1 << n); i ++){
    	valid[i] = 0;
        f[i] = 0;
        vis[i] = 0;
    }
    for (int i = 0; i < n; i++) {
        cin >> xa[i] >> ya[i] >> xb[i] >> yb[i];
        xa[i] = min(xa[i], w);
        xb[i] = min(xb[i], w);
        ya[i] = min(ya[i], h);
    	yb[i] = min(yb[i], h);
        ya[i] ++;
        yb[i] ++;
 		nums.emplace_back(ya[i]);
 		nums.emplace_back(yb[i]);
    }
    std::sort(nums.begin(), nums.end());
    nums.erase(std::unique(nums.begin(), nums.end()), nums.end());
    sz = nums.size() - 2;
    if (!check((1 << n) - 1)) {
    	cout << "-1\n";
    	return;
    }
    for (int i = 0; i < (1 << n); i++) {
        valid[i] = check(i);
        f[i] = 0;
        vis[i] = 0;
    }
    cout << dfs(0) << '\n';
}
int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    inv[0] = inv[1] = 1;
    for (int i = 2; i < N; i++) inv[i] = (MOD - MOD / i) * inv[MOD % i];
    cin >> TT;
    while (TT--) Solution();
    return 0;
}