压印字符识别
转载自https://blog.csdn.net/woshilicong33/article/details/54234261
分享一个前段时间做的一个小东西吧,很简单,就是压印字符识别,当时老师的想法是想快速测量汽车发动机上边的型号,识别上边的字符,但是我们在实验室也没有买一台发动机过来,我就用3D打印机打印了一个不同高度的字符,其实方法很简单。就是利用高度调制余弦光栅相位变化,测相位变化量对应高度的关系,然后在同意一高度上抽取字符信息,然后扔到matlab里边就能识别,大概方法就是这样,获取相位展开这部分参考的是一篇论文《
Improved method for phase wraps reduction inprofilometry
》这个相位展开方法有一个缺陷就是高度超过2pi的是不 能完全展开的,但是我们的压印字符与背景的高度差很小,所以这种方法是完全适合的,而且速度很快,只要进行一维傅里叶变换就可以了,目前很多方法都是用的二维傅里叶变换,然后再逆变换回来,那样也可以得到,但是速度肯定是没有进行一维傅里叶变换来得更快,我们是不需要进行逆变换的。就当以上是一个摘要吧
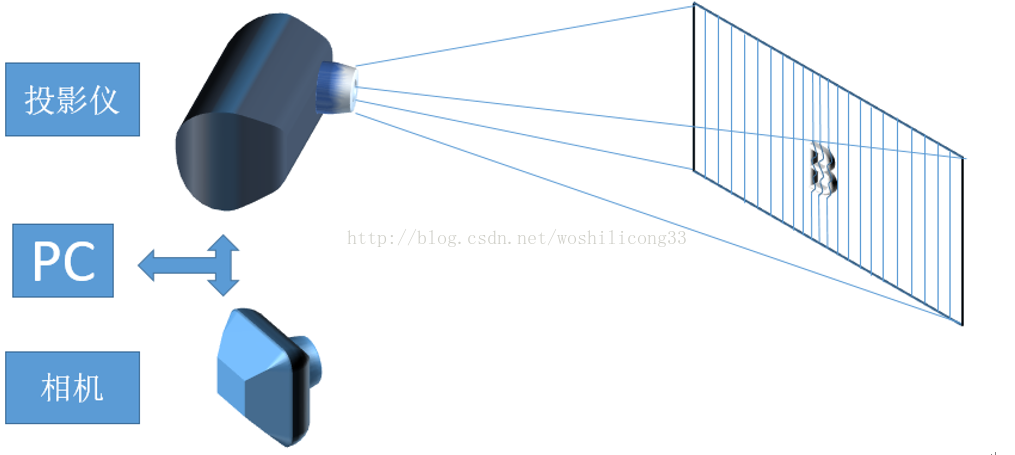
首先先讲讲基本算法。看一下结构图。
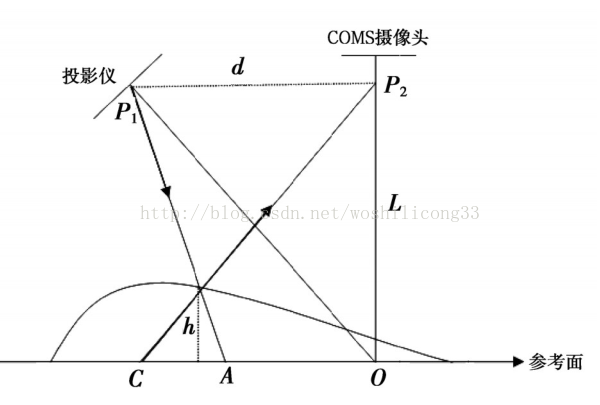
突起部分是被测表面,由于物体高度调制作用,原本打在A的光变成了C点的信息,如果我们投射结构光,那么接收的图像会有一个错位的变化,结构光选择余弦光栅,接收图像的变化就变成余弦光栅相位的变化。投影仪光心与摄像头的光心水平距离为 d ,两光心的水平线与参考面平行,摄像头与参考面的垂距离为 L 。当投影仪的出射光照射到参考平面的 A 点时,由于受到高度调制作用使照射在 A 点的光转移至 C 点。若设物体D点的高度为 h ,则由三角原理可得:
这样就建立了相位和高度的对应关系,下一步的关键就是获得相位信息。由于正弦光栅投射到漫反射物体表面后,COMS相机获取的变形栅像可以表示为:
式中, R( x , y ) 表示所测物体表面的不均匀分布反射率, A ( x , y)是背景强度, B ( x , y )/A( x , y ) 表示光栅条纹的对比度。 φ ( x , y)是相位值。采用移相的方法则可以比较准确的获取相位值,在相移法中,每次移动光栅周期的1/4,因而相移量为 π 2 。采集到的对应的四帧条纹图分别为:
此时获得的相位信息并不是真实的相位,因为反tan是一个周期函数,所以下一步就获得真实相位,也叫相位展开或者解包裹或者什么什么的。。。。
相位展开的方法就是用的Guangliang Du1等人的论文。想看英文原版的可以自己去下载,我就简单说一下原理。也是很简单的。得到折叠相位图像之后选取图像非字符区域的一行和一列,通常为第一行第一列。在选取的两个一维向量的两端进行补零操作具体公式为:
根据傅里叶变换的频移特性可知:
所以获得频移后的相位信息图像则可以进行移频计算:
只需要获得频移后的图像信息,所以不需要进行2维傅里叶变换和2维傅里叶逆变换,只需要进行如下计算即可:
所以相位信息即可由下列公式获得:
至此我们就得到了真实的相位信息,总结起来就很简单了,其实就是获取折叠相位背景的横纵频率,找到基频位置,把图像转换到复数域之后整幅图像根据横纵方向的基频进行移动,这样就把背景给滤掉了,只剩下字符的相位信息。来说一下实测过程。
结构图
被测字符
被测物体,有人看到被测物体说我这个环境要求太高,背景都是黑色的,其实不是这样的,这跟打光和光圈调节有关系,而且我们的误差也不在黑色部分,而是那个白色的背景才是干扰部分,黑色部分没有我们需要的信息,首先设置感兴趣去就是那个正方形的白色字符,然后投射四幅相位差是pi/2的余弦光栅。获得折叠相位。
这是折叠相位的图像,因为我们投射光栅的频率比较低,字符的板子又比较短所以打在字符上的光也很少,我们提取感兴趣之后,字符板子上只有不到2个周期的光栅,当然这是不影响测量的,只是看着不太好看。
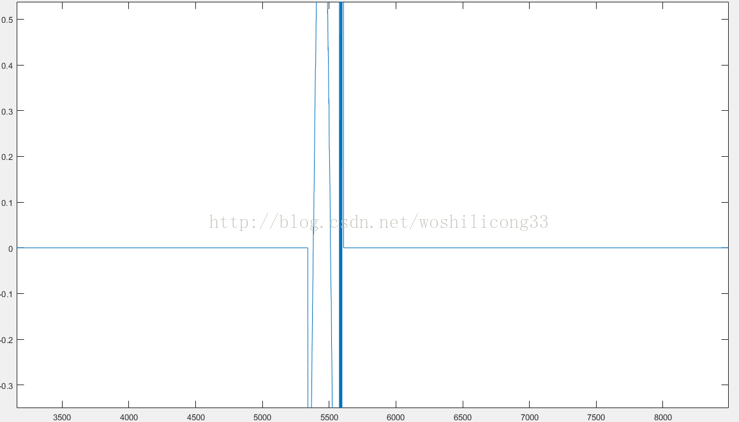
下一步就是提取第一行和第一列的数据然后进行补零操作,这一步的补零目的就是提高傅里叶的采样频率,这样可以提高基频位置的精度。补零很简单了,中间是数据,两边就是零。下图
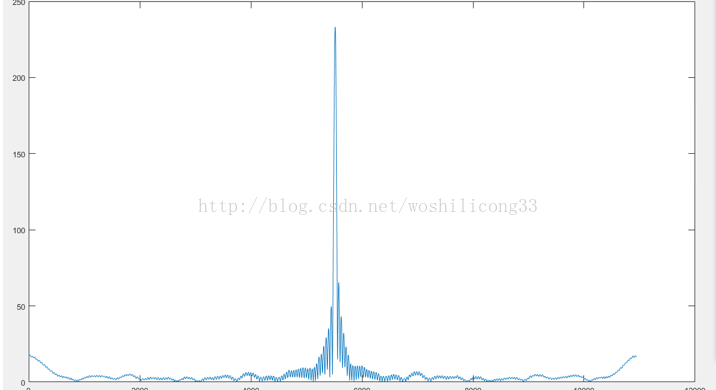
然后进行傅里叶变换,算横纵两个方向的基频,傅里叶变换之后的图像。
找到两个方向的基频,把图像转换到复数域之后,进行频移变换。就可以得到字符的相位信息。
这是三维的图像,再看一下灰度的图像。
中间的字符部分的灰度值比较高,高度不同的三行字符,他们的灰度值也是不同,此时灰度值反应的就是字符的高度信息。选取不同的阈值进行滤波就可以得到字符信息。
v6-fsi 是高度1mm的字符,下边的bosch是3mm的字符,设定不同阈值选取不同高度下的字符。然后直接让matlab去识别就好了,那就是很传统的方法我就不说了。这里边我这个效果还不是很好,这里边我能想到几个原因,首先就是我们拍摄的距离比较远,而相机的像素也不是很高,所以很多细节都拍不到的。因为相位对高度是很敏感的,我们用肉眼都很难分辨相位的变换,还有一个问题就是我们的光栅频率比较小,理论上光栅频率越大我 们能分辨的细节越多。我们实验室用相位的方法都可以测量出指纹的高度。很精密的东西。最后看一下matlab的代码。很多人可能可以看懂公式但是没办法把公式别称代码,这个是需要多加练习就可以。很简单也就是六十多行。
thre=0.1; %滤波二值化阈值
fs=1; %操作图像放缩比
A0=double(rgb2gray(imread('D:\222\0.JPG')))/255;
A1=double(rgb2gray(imread('D:\222\L1.JPG')))/255;
A2=double(rgb2gray(imread('D:\222\L2.JPG')))/255;
A3=double(rgb2gray(imread('D:\222\L3.JPG')))/255;
A4=double(rgb2gray(imread('D:\222\L4.JPG')))/255;
A0=im2bw(A0,thre);
imshow(A0);
h = imrect;
position = wait(h);
A2_4=A4-A2;
A3_1=A1-A3;
a1=atan2(A2_4,A3_1);
imshow(a1);
a1=double(A0).*a1;
a1=imresize(a1,fs); %可选
imshow(a1);
a1=imcrop(a1,position);
imshow(a1);
li=1;
[m,n]=size(a1+pi);
fwc=cos(a1)+1i*sin(a1);
fwc1=[zeros(1,20*n),fwc(li,:),zeros(1,20*n)];
fwc2=[zeros(20*m,1);fwc(:,li);zeros(20*m,1)];
fx=fft(fwc1);
[fxm,fxn]=max(fx);
fxn=(fxn-1)/41;
fy=fft(fwc2);
[fym,fyn]=max(fy);
fyn=(fyn-1)/41-(fyn-1)/41;
for k=1:m
for j=1:n
x3(k,j)=fwc(k,j)*exp(-1i*2*pi*((fyn)*(k-1)/m+(fxn)*(j-1)/n));
end
end
y1=atan(imag(x3)./real(x3));
figure;
mesh(-y1);
y2=-y1;
[m1,n1]=size(y2);
OutImg = Normalize(y2);
mesh(OutImg);
for k=1:m1 %1:m
for j=1:n1 %1:n
if OutImg(k,j) > 170
Fc3(k,j)=1;
else
Fc3(k,j)=0;
end
end
end
figure(2);
imshow(Fc3);
ocrResults = ocr(Fc3);
recognizedText = ocrResults.Text;
imshow(Fc3);
text(10,50,recognizedText,'BackgroundColor',[1,1,1]);
title('识别字符');



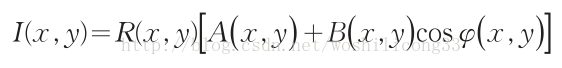
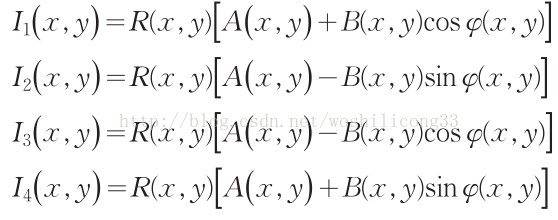
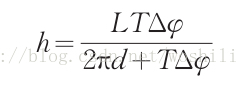

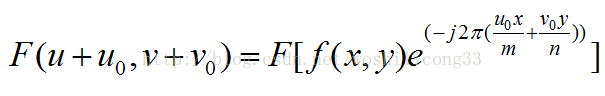
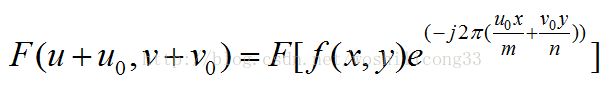
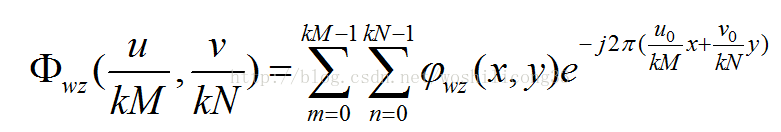
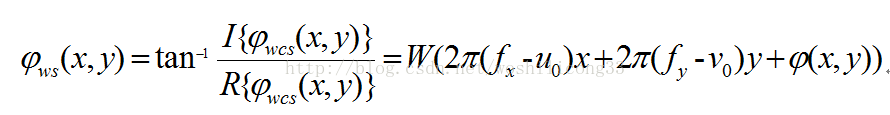





 浙公网安备 33010602011771号
浙公网安备 33010602011771号