模拟Paxos算法及其简单学习总结

一、导读

Paxos算法的流程本身不算很难，但是其推导过程和证明比较难懂。在Paxos Made Simple[1]中虽然也用了尽量简化的流程来解释该算法，但其实还是比较抽象，而且有一些细节问题没有交代，读完也只能了解到算法的一个大致轮廓。在《从Paxos到Zookeeper 分布式一致性原理与实践》[3]中也讲到Paxos算法，但是其行文思路也是延续了原论文，没有一个具体的实例来帮助读者理解。

第一次我也没看懂，后来觉得，可能是我学习的方式不对。通常而言，都是在已经成熟的问题抽象和逻辑推理之上去理解算法的，理论层面的概念模型为算法赋予灵魂，但往往不够具体因而不易理解；相对而言，恰当的算法模拟可以为赋予算法血肉，理解算法最好的方式就是手动模拟。两方面都很重要，适当结合往往能够理解得更深刻。本文也试图先梳理Paxos算法的流程，然后特意构造一些实例去模拟算法的场景，从实例的角度去理解该算法。

本文省略掉不必要的基础的介绍，尽量直接的进入主题。内容范围仅限于the The Basic Paxos Algorithm，不讨论Paxos算法家族的其他变种。接下来的第二节是针对各角色的信息保持、算法流程的梳理和简单约定，在第三节会构造一些实例，并结合算法流程去模拟该算法，第四节会简单总结该算法重要特性，在最后会引入一些参考资料。

二、信息保持及算法流程

2.1 关于提案及Acceptor和Proposer的信息保持

首先这里的提案(proposal)是一个抽象的概念。具体可以是“推选某个节点为Leader”或者“将某个值更新为另一个值”，甚至是“将某个更新操作更写到日志系统中”等等。

在后面的算法模拟中，提案由一个提案编号和提案值(Value)组成：[N,Value]。Paxos算法以轮次的形式进行，也即每轮以一个全局唯一的自增编号发起。轮次与提案编号呼应，即在第K轮次中，在满足一定条件的情况下会产生编号为K，提案值为VK的提案：[K,VK]。

如果某个提案在某轮次中被某超过半数的Acceptor批准，则该提案被选定。

其次Acceptor和Proposer都需要保持一些必要的信息，并会更新这些信息。

Acceptor保持的信息为：RoP_Max，RoA_Max和Value_Acc。

其中：

RoP_Max含义是某Acceptor参与的最大轮次（the max round of participation），相当于原论文中的rnd[a]，初始为0。

RoA_Max的含义是某Acceptor已批准的提案的最大轮次（the max round of acceptance），相当于原论文中的vrnd[a]，初始值为0。

Value_Acc代表被当前已批准的提案，相当于原论文中的vval[a]，初始为NULL。

注意：这里参与的含义可能是在P1-B阶段Acceptor对某伦次提案请求的响应，也可能是在P2-B阶段Acceptor批准了某轮次的提案，因此这两个阶段均会更新RoP_Max。

不难得知，这里的RoA_Max和Value_Acc组合可以得到某伦次被批准的提案：[RoA_Max,Value_Acc]。

其初始状态如下：

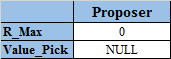
Proposer保存的信息为R_Max和Value_Pick。

其中：

R_Max表示某Proposer发起的最大轮次号，相当于原论文中的crnd[c]，初始值为0。

Value_Pick表示Proposer在P2-A阶段挑选的提案值，相当于原论文中的cval[c]，初始值为NULL。

R_Max和Value_Pick组合可产生一个提案：[R_Max,Value_Pick]，当然不是每轮都具备条件产生一个提案。

其初始状态如下：

2.2原论文中的算法流程

在Paxos Made Simple[1]中算法流程分为两阶段：

Phase 1：
(a) A proposer selects a proposal number n and sends a prepare request with number n to a majority of acceptors.-->记作P1-A
(b) If an acceptor receives a prepare request with number n greater than that of any prepare request to which it has already responded,then it responds to the request with a promise not to accept any more proposals numbered less than n and with the highest-numbered proposal (if any) that it has accepted.-->记作P1-B

Phase 2：
(a) If the proposer receives a response to its prepare requests (numbered n) from a majority of acceptors, then it sends an accept request to each of those acceptors for a proposal numbered n with a value v, where v is the value of the highest-numbered proposal among the responses, or is any value if the responses reported no proposals.-->记作P2-A
(b) If an acceptor receives an accept request for a proposal numbered n, it accepts the proposal unless it has already responded to a prepare request having a number greater than n.-->P2-B

上述四个阶段可以分别简记为：P1-A，P1-B，P2-A，P2-B。

以上算法流程提供了一个初步的算法轮廓，有很多细节问题没有交代。因此仅仅依靠以上的信息，并不能够完全去模拟出一个具体的算法实例。

在Fast Paxos[2]中的Section 2:The Classic Paxos Algorithm中作者给出了一个比较具体的算法流程（少数单词已根据本文语境做替换）：

P1-A:
If R_Max < i, then proposer starts round i by setting R_Max to i,setting Value_Pick to NULL, and sending a message to each acceptor a requesting that a participate in round i.
P1-B:
If an acceptor a receives a request to participate in round i and i > RoP_Max, then a sets RoP_Max to i and sends proposer p a message containing the round number i and the current values of RoA_Max and Value_Acc.
If i <= RoP_Max (so a has begun round i or a higher-numbered round), then a ignores the request.

P2-A:
If R_Max = i (so p has not begun a higher-numbered round),Value_Pick = NULL (so p has not yet performed phase 2a for this round), and p has received phase 1b messages for round i from a majority of the acceptors; then by a rule described below, p uses the contents of those messages to pick a value v, sets Value_Pick to v,and sends a message to the acceptors requesting that they vote in round i to accept v.
P2-B:
If an acceptor a receives a request to vote in round i to accept a value v, and i >= RoP_Max and RoA_Max != i; then a votes in round i to accept v, sets RoA_Max and RoP_Max to i, sets Value_Acc to v, and sends a message to all learners announcing its round i vote.
If i < RoP_Max or RoA_Max = i (so a has begun a higher-numbered round or already voted in this round), then a ignores the request.

以上流程应该是比较精确的描述，英文本身的内容也不难理解，不再需要过多的翻译。本文也会遵循这个流程去模拟一些实例。

2.3 本文对算法流程的约定。

为方便后文的陈述，对以上各阶段中涉及的过程做恰当的约定，同时尽量与大多数介绍Paxos算法的文章说法保持一致。

1、为方便起见，各阶段的消息通信以(X)或者(X,[Y,Z])或者([Y,Z])的形式表示，具体视情况而定。

2、P1-A中Proposer向Acceptor集合发送的提案请求称作Prepare请求，消息内容包括轮次号N：(N)。

3、P1-B中Acceptor的响应Proposer的过程称作Promise响应，消息内容包含轮次号和某提案（=提案编号+提案值）：(N,[K,VK])。

其中N的含义是Acceptor向Proposer保证该自己不会批准（Accept）任何编号小于N的提案。

4、P2-A中Proposer向Acceptor集合发送批准请求称作Accept请求，消息内容是一个提案：([K,VK])。

三、实例及算法模拟

3.1 一个最基础实例

假设有5个Acceptor，1个Proposer。其初始状态下如上文中的列表所示。

1）按照P1-A约定，Proposer发起轮次为1 的Prepare请求；

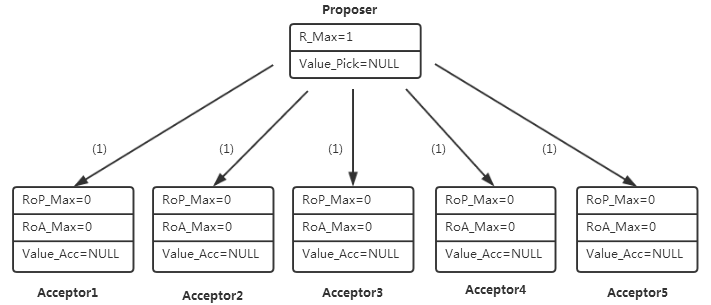
2）假设所有Acceptor均收到请求，按照约定P1-B，满足1大于所有Acceptor持有的RoP_Max值的条件，于是将自己的RoP_Max值设置为1，所有的Acceptor均响应Prepare请求，此时所有的Acceptor之前并未批准任何提案。

3）假设Proposer收到了所有的5个Acceptor的Promise响应，按照P2-A的约定，收到响应的数量已经超过Acceptor集合的半数，同时由于之前并未存在批准的提案，Proposer可以任意选择一个提案值，这里暂且记为选择了V1这个提案，Proposer应该发送Accept请求，希望Acceptor集合批准该提案。

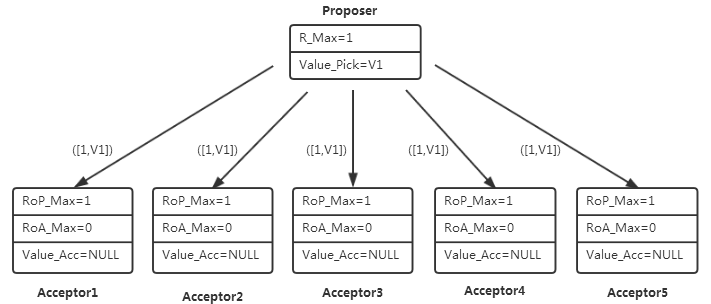
4）假设所有Acceptor均收到了Accept请求，按照P2-B的约定，5个Acceptor尚未参与任何编号比1更大的提案（此时只存在一个Proposer且之前只发起了一轮提案），所以所有Acceptor应该批准V1这个提案，批准之后Acceptor的状态如下：

至此，[1,V1]这个提案被半数以上的Acceptor批准，所以[1,V1]是一个被选定（chosen）的提案，V1是被选定的提案值。

3.2 异常情况下算法的工作流程

上一小节的基础实例是在理想情况下的情形，而实际情况要复杂很多，例如网络拥塞导致消息延迟或者乱序、网络分化导致消息不可达、Acceptor和Proposer本身宕机等等，这些异常情况要求该算法要有比较好的容错性。实际上整个分布式系统设计讨论的几个核心要点之一就是针对各种异常情况下的系统容错性。

以下讨论一些典型的异常情况下Paxos算法如何正确的工作。

仍然假设有5个Acceptor，1个Proposer。

1）初始状态

Acceptor集合持有状态：

Proposer持有状态：

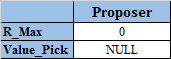
2）Proposer发起第一轮Prepare请求；假设由于暂时网络中断或者网络分化等网络异常，只有Acceptor1和Acceptor5收到了提案请求，这两个Acceptor正常响应Prepare请求。

3）Proposer收到了这两个响应，此时根据P2-A的约定，响应数不足半数，不具备发送Accept请求的条件，于是Proposer重新发起第二轮Prepare请求。假定这次有四个Acceptor收到了请求，唯独发往Acceptor1的请求丢失了。成功收到消息的四个Acceptor给予正常响应。

4）Proposer也成功收到了四个响应，根据P2-A的约定，Proposer任选一个提案V1发送Accept请求：(2,V1)。但是Acceptor集合中只有Acceptor2和Acceptor3两个收到了这个Accept请求。此时[2,V1]只被两个Acceptor批准，目前为止仍然没有任何一个提案被选定。

5）Proposer发起第三轮提案Prepare请求，全部的Acceptor收到了提案请求，并给予响应。

6）Proposer收到全部的响应，应该评估这些响应，并从中响应的提案中挑选一个提案值。此时根据P2-A的约定，挑选的应该是最大的RoA_Max所对应的提案值。max{0,2,2,0,0}=2，对应的提案是V1，因此Proposer在本轮挑选的提案值为V1。Proposer向Acceptor集合发送Accept请求:[3,V1]，假设这次有Acceptor1，Acceptor3和Acceptor5收到了Accept请求并批准了该提案。

到目前为止，进过3轮，[3,V1]提案已经被超过半数的Acceptor批准，因此被选定。其实上述讨论的过程中，每个过程都有可能存在消息丢失，而消息丢失的原因也可能是多种多样，并不仅仅指因网络原因造成的消息丢失，例如节点短时间宕机也可以归为这里的消息丢失。

实际上，在网路通信情况较差的情况下，即便进过多轮次，仍然有可能得不到一个选定的提案，无论是3个Acceptor还是5个Acceptor或者说更多的Acceptor构成的集合，可以很容易的构造出这样的场景，关键是Acceptor接受提案的环节（P2-B阶段）直接影响了该算法的最终结果。

3.3 关于时序问题

以上虽然只是讨论了只有一个Proposer的情形，并且是假定了每轮结束后（来自Acceptor的响应不足半数以上或者在Acceptor集合批准某提案后仍然不能选定某个提案）才发起下一轮的提案请求。实际上，两轮提案完全可以允许异步进行，基于该算法Acceptor集合在P1-B和P2-B对提案编号的判定和约束，如果Acceptor在Promise响应（对于P1-B）或者接受（对应P2-B）某轮次为M的提案时，发现自己在之前已经响应了比M更大轮次的提案，则M这一轮次的提案实际上已经失效了，被更高轮次的提案所抢占。所以只要保证一个全局不重复的提案编号（轮次编号），按照该算法的约定，就能够保证该算法的正确性，但可能需要进行更多轮次才能选定一个提案。

更进一步，如果存在多个Proposer的情况，每个Proposer多都能在任意时间点发起提案请求，似乎有可能出现上面提到的“轮次抢占”的现象。比如多个Proposer如果按照一定的节拍交叠地在P1-B这个阶段轮流“抢占”，会出现所谓的“活锁”现象。

3.4 “活锁”现象

如果允许同一个Proposer交叠的发起提案请求，考虑如下一种情形：

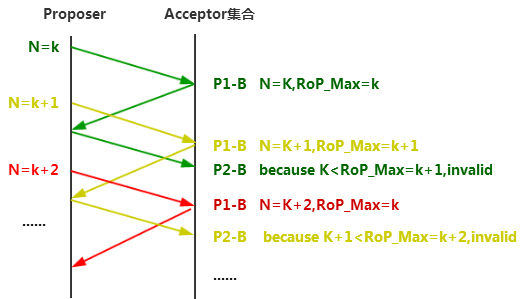
如上图所示，不同的颜色代表同一个Proposer在不同时间点发起的不同轮次。所有的轮次均在P2-B阶段被Acceptor集合认为无效，因为在收到该轮次的Accept请求之前不久，Acceptor集合响应了一个更高轮次的提案，导致RoP_Max变大。如果一直按照这个节拍发起后续的轮次，那么陷入一个“死循环”，永远无法选定一个提案了，尽管在真实的场景中这种情况发生的概率很小。

尽管理论上存在这种情况，但是实际上可以很容易的对Proposer施加约束来规避这种情况。例如可以约定针对某个Proposer发起的某一轮次的提案请求，只有确定该轮次为无效被丢弃后，同一个Proposer才能发起下一轮次的提案请求。

理解了上述过程，在多个Proposer存在时导致“活锁”现象与之类似，很容易构造一个场景来重现“活锁”现象，只需要让不同的Proposer轮流发起提案请求即可，如下所示。

3.5 关于Pcik a Value规则

假设在第K轮次，提案[K,VK]被超过半数的Acceptor批准，那么这个提案就认为被选定，并且在以后的轮次M（M>K）中，根据挑选Value的规则，在P2-A阶段，Proposer只能够挑选VK，因此只能组成[M,VK]形式的提案希望Acceptor集合批准。

因此，即使在多轮Paxos算法过程中，有可能会存在多个提案被选定，但是这些被选定的提案值必定是相等的。从某种角度来说，要达到要取得一致意见，达成共识的目的，实际上要求的是针对某提案值Value达成共识，而提案编号为提案值披上了一层外衣，使我们更好的进行算法的处理。

原论文中关于Pcik a Value的规则如下：

Pcik a Value的规则可以说是该算法的核心，也是保证了该算法安全性的关键。

假设有3个Acceptor，一个Proposer，这次以某一个中间状态开始讨论。

Acceptor当前状态（达到这种状态是完全有可能的）：

1）Aroposer以N=3发起第三轮Prepare请求：(3)，Acceptor1和Acceptor3收到请求，并作出响应。

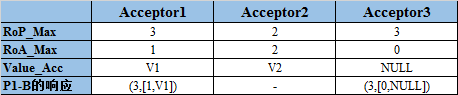
2）Proposer成功收到响应，发起Accept请求：[3,V1]，但只有Acceptor1和Acceptor3收到了Accept请求，满足批准条件。

此时，提案[3,V1]已经被Acceptor1和Acceptor3批准，被视为选定的提案。然后如果再以N=4发起新一轮的提案请求，在第4轮的P1-B阶段，Proposer只有在收到2个Promise响应的条件下才具备发起Accept请求的条件。而根据Pick a Value的规则，无论怎么组合两个Promise响应，其RoA_Max最大值只能是3，其对应的Value只能是V1，只能是V1有资格被挑选出来在P2-A阶段与轮次4组成新的提案:[4,V1]，不可能是V2。V1在第4轮结束后定会被超过半数的Acceptor批准，这一情况无法被改变。

讨论更一般地情况：

不失一般性，这里假设在顺利完成第K轮提案之后，提案[K,VK]被超过半数Acceptor批准从而首次被选定，在1到K-1的各轮次中，尚未有一个提案被选定。

那么在第K轮的P1-B阶段，必定有超过半数的Acceptor响应了Proposer的Prepare请求，响应Prepare请求的集合中每个Acceptor都将自己的RoP_Max更新为K。

Proposer也必定收到了超过半数的Promise响应，否则无法发起Accept请求。然后Proposer挑选了VK，顺利发起了Accept请求：([k,VK])。（注意：因为前面已经设立了第K轮后VK被选定的题设，故这里Accept请求中必定是VK无疑，VK并非特指某一个提案，可以是任意一个，具有任意性。）

超过半数的Acceptor收到Accept请求，更新自己的RoP_Max和RoA_Max为K，Value为VK，然后VK被批准的数量超过半数，被选定。

至此，其实已经有了一些隐含其中的细微逻辑可以发掘。考虑将RoA_Max=K的Acceptor集合记为集合S，将Value=VK的集合记为集合T。显然，两个过半的集合必定有重叠，至少重叠一个。“超过半数”的发现对于接下来的推论其实很重要。

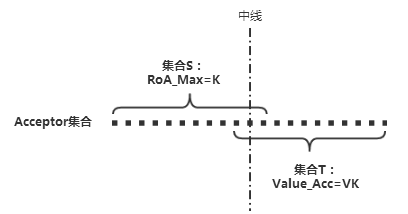
接下来发起第K+1轮的Prepare请求：(K+1)，假设这一轮也很顺利。

Proposer收到超过半数Acceptor的Promise响应，记这些半数以上的Acceptor集合为Q。此时可以断定，所有的这些Promise响应中，由RoA_Max组成的集合中最大值必定为K，因为集合S与集合Q的交集必定至少有一个公共元素。同时，这个RoA_Max=K的Promise响应中Value必定为VK，因为这就是在第K轮被集合S中每个Acceptor批准的提案。因此根据P2-A的约定，第K+1轮被挑选出来的Value是VK，该轮产生的提案是[K+1,VK],发送该提案希望Acceptor能够批准，当然在该轮的P2-B阶段，可能没有一个Acceptor批准VK（所有消息均丢失），也有可能某些Acceptor批准了VK。总之，经过第K+1轮之后，批准VK的Acceptor不会比第K轮减少，只会越来越多。

按照以上的逻辑，继续往更高的轮次推演，超过半数的Acceptor批准VK这个结论已然成立，由此保证该算法的安全性。

当然以上逻辑只是一个直白的、非正式的推理，但能够说明部分问题。更精准的证明可以看论文。

3.6 Learner学习被选定的提案

Learner学习的目的就是需要找出某一个超过半数的Acceptor批准的提案。要实现这一目的，最简单的办法是一旦Acceptor批准了一个提案，就将该批准的提案告知每一个Learner，显然从通信次数的角度来看，这样有点麻烦，至少需要Count(Acceptor)XCount(Learner)次通信才能确定被选定的。

稍微改进一下，可以选一个主Learner（原文中称作a distinguished learner），Acceptor只需要与这个主Learner通信，再由这个主Learner去通知其他的Learner。这种改进方法存在单点故障，缺乏可靠性。所以通常，需要一个主Learner的集合来解决可靠性的问题。

四、一点总结

1）Paxos算法在网络通信比较好的情况下能够快速高效的让一个提案被半数以上的Acceptor接受，选定一个提案，从而达成一致意见。

2）Paxos算法的容错能力是2F+1。即在总共有2F+1个服务端的情况，只要不超过F个服务端同时出现损毁，该算法就能够正常运作。

2）采用“超过半数”的机制，保证在某轮次只能有一个提案没选定，采用Pick a Value规则挑选提案值，保证不同的轮次只能有一个提案值被选定。不同的轮次可能有不同的提案被选定，但是这些选定的提案仅仅是提案编号不同，其提案值必定相同。

4）当某个提案被选定，那么从此以后，所有的Acceptor只能批准该提案值，这是由Pick a Value的规则保障的。

5）假设所有的Acceptor都接批准某个提案值，将这些提案值的集合记为S（例如S={V1，V2，V3}），那么，即使现在尚未有提案值被选定，但是可以肯定，在将来被选定的提案值一定是集合S中的某一个提案值，绝不可能是其他的提案值了，保证了一种“封闭”特性。保证这个特性的正是P1-B中Acceptor响应给Proposer时的约束：Acceptor只会将自己曾经批准的提案中最高编号的提案响应给Proposer。举例来说，对于5个Acceptor来说，排除冗余情况，Proposer最多只有三次能够任选提案值的机会（收到所有的Promise响应中均为NULL并且Accept请求存在消息丢失），考虑任选提案值也有可能会选择到相同的提案值，因此集合S最多只能有三个不同的提案值。更一般的，当Acceptor集合的大小为奇数R时，集合S的大小最多为R/2+1。