矩阵链乘法问题
问题描述:
给定n个矩阵的链<A1,A1,A3...An>,矩阵Ai的规模(行列)为pi-1xpi(1<=i<=n),求矩阵链的完全括号化方案,使得矩阵乘积A1A2A3...An所需的标量乘法次数最小(假定所给举证链满足相容性,能够正确的进行矩阵运算)。
注:假设矩M的规模为pxq,矩阵N的规模为qxr,那么,矩阵乘法MXN的标量乘法次数为pqr。
分析:
重点在于分析其最优子结构性质,并且导出递推公式。
有j-i+1个矩阵,进行矩阵链乘:AiAi+1Ai+2..AkAk+1...Aj-1Aj,假设其最优括号化方案在Ak这个地方划分,则整个Ai到Aj矩阵链的最低代价三部分相加:
1、前半部分分矩阵链AiAi+1Ai+2..Ak(其连乘后的结果是规模为pi-1xpk的矩阵)的最低代价;
2、后半部分矩阵链Ak+1...Aj-1Aj(其连乘后的结果是规模为pkxpj的矩阵)最低代价;
3、pi-1xpk阶的矩阵与pkxpj阶的矩阵相乘的标量乘法次数:pi-1pkpj。
但是是Ak这个分割点是不定的,在Ai到Aj(出Aj外)之间的每矩阵都有可能作为这个最有的划分点。因此需要找出在遍历意义下的最小代价。
假设C(i,j)是这些矩阵链乘的最小代价,那么递推式
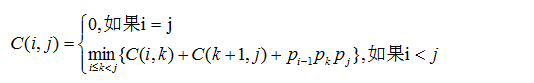
另外,对于输入数据的处理,因为矩阵链都是相容的,所以实际上可以用一个一维数组存储依次存储每个矩阵的行列数(要去重)。
例如矩阵链A1...A6如下:

可以用一维数组p来存储:
int[] p = {30,35,15,5,10,20,25};
A1的规模可以表示为:p[0]xp[1]
A2的规模可以表示为:p[1]x[2]
更一般的,Ai的规模可以表示为p[i-1]xp[i]
算法实现:
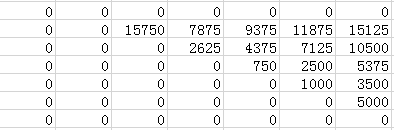
package agdp; public class Matrix { public static int getMinCost(int[] p){ int n = p.length-1;//n为矩阵链中矩阵的个数,等于p长度-1 int[][] aux = new int[n+1][n+1];//辅助数组,为方便计算,第0行和第0列不利用 for (int l = 2; l <= n; l++) {//矩阵链的长度,从2开始,一直到长度为n结束,满足l=j-i+1 for (int i = 1,j; i <= n-l+1; i++) {//当j=n是,i到最大值,所以i<=n-l+1 j = i+l-1; aux[i][j] = Integer.MAX_VALUE; for (int k = i; k < j; k++) {//遍历Ai到Aj矩阵链中每一个位置,并存储最小者 aux[i][j] = Math.min(aux[i][k]+aux[k+1][j]+p[i-1]*p[k]*p[j], aux[i][j]); } } } return aux[1][n]; } public static void main(String[] args) { // TODO Auto-generated method stub int[] p = {30,35,15,5,10,20,25}; int result = getMinCost(p); System.out.println(result); } }
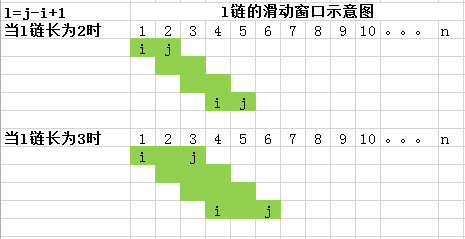
不同的l=j-i+1链的长度会导致l先链从做到右形成一个“滑动窗口”。
其计算过程中全部的子问题的解都存储在aux数组中,该aux中有效数据是一个上三角矩阵。