网络流初步
网络流初步(脑部整理)
呜呜呜,家人们也是学上网络流了。
咸鱼起手,你反应得过来吗?
英语不太好(老英不会看窝博客吧)
What is 网络流?
概述
网络
是指一个特殊的有向图 ,其与一般有向图的不同之处在于有容量和源汇点。
中的每条边 都有一个被称为容量 的权值,记作 。当
时,可以假定 。 中有两个特殊的点:源点 和汇点 。 对于网络
,流 是一个从边集 E 到整数集或实数集的函数,其满足以下性质。
- 容量限制:对于每条边,流经边的流量不得超过该边的容量,即
; - 流守恒性:除源汇点外,任意结点
的净流量为 。 其中,我们定义
的净量为 。对于网络 和其上的流 ,我们定义 的流量 为
的净流量 。作为流守恒性的推论,这也等于 的净流量的相反数 。对于网络 ,如果 是 的划分(即 ),且满足 ,则我们称 是 的一个 割(cut)。我们定义 割 的容量为 。
--以上摘自
靠! 什么玩意?都是中文咋看不懂?
于是我们找到了启蒙例(ti)题(jie)。然后偷税得发现,其实就是一堆的水管,每个水管有相应的容量头大有趣问题。
可以发现,对于一张网络,有这么几个重点。
- 容量限制:
。一条边上的流量不能大于水管容量( 不然就要爆炸)。- 相反净流量:
由 到 的净流量必须是 到 净流量的相反数。 - 流守恒性:除非
或 ,否则 。一个非源非汇的点的净流量一定是 。
最大流
根据名字显然可以知道最大流就是最大流量的意思
其实就是以下意思:
【模板】网络最大流
题目描述
如题,给出一个网络图,以及其源点和汇点,求出其网络最大流。
输入格式
第一行包含四个正整数
接下来
输出格式
一行,包含一个正整数,即为该网络的最大流。
样例 #1
样例输入 #1
4 5 4 3
4 2 30
4 3 20
2 3 20
2 1 30
1 3 30
样例输出 #1
50
提示
样例输入输出 1 解释
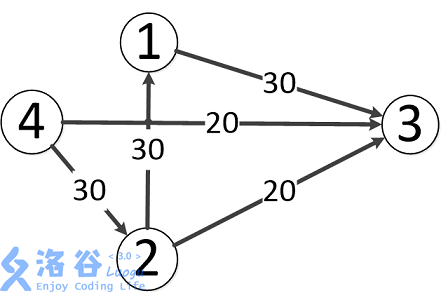
题目中存在
故流量总计
数据规模与约定
- 对于
- 对于
青铜 — — Ford-Fulkerson算法(增广路算法)
首先我们先找到一条从增广路,然后把一条条增广路搞加在一起,似乎就可以得到一个答案。
但如果选择的路径较劣就会影响最后的答案。
那怎么办呢?增广路真的一点鸟用都没有吗?
当然,部分人类凭借高级的大脑想出了处理方法——建一条反方向的钟边。正向边减少的同时给反向边进行增加,即利用残量网络的概念。可以理解为把满流的边扔掉后,边权为剩余流量的图。(包括反向边)。当在残量网络中流过一条反向边时,相当于将原先的流压了回去,而通过列举简单的例子,可以发现流经反向边事实上是一个反悔的等价操作。
每次只需要在残量网络中找增广路即可。
局限性
但这样跑肥肠靠RP,只需要简单造造数据就可以把算法卡成
那这算法有个蛋用啊?表演T飞吗?但这个算法可以打暴力通过合理优化达到高效的运行。但增广路算法是基础。
Edmonds-Karp算法(EK算法)
显然地,我们可以每次增广最短路,把最短路压榨干净后,这条路就在残量网络中OUT了。而这条跑满流的边也就是关键边。
每一个增广路意味着至少有一条关键边出现,而增广过程的迭代次数也就可以看做是每条边成为关键边的次数。
这样总迭代次数为
局限性
因为
这时候就有人说了:虽然复杂度已经降到了一个多项式的程度,但还是难以让人接受,有没有更快更好的算法呢?
有的,有的,包有的兄弟。
咱先想想EK为啥不够快:
我们可以很显然地艰难地发现,EK每次只会跑一条最短路,但我们最短路可能不止一条啊。
基于这一点,我们继续进行优化。
Dinic算法
没有什么是一个BFS或一个DFS解决不了的;如果有,那就两个一起。
Dinic的核心思想就是在EK的基础上进行多路增广。
这需要搞出分层图,而这里分层图的定义可以理解为:对于每个点,到达源点s的最短路大小。也可以认为是一个点的深度。
分完层之后有什么好处呢?首先层内边和反向边都会被无视掉。
其次我们可以发现,此时所有的最短路都在图上呈现。这样DFS一遍就能把这张图上的最短路全都干掉。
似乎这样可以跑得飞快。
但是的但是,我们会重复搜到同一个点,但通过这个点的流量不一定已经到达最大值,所以不能直接标记掉,但无标记的DFS直接爆炸。
so 优化了个寂寞???
No!No!No!
我们再来加两只优化(咋这么多优化)。
代码解释。
struct node{int to,c,lp;};
vector<node>g[N];
int dep[N],pos[N];
int n,m,S,T;
inline void add(int from,int to,int c)//存边包括正向边和反向边
{
g[from].push_back((node){to,c,(int)g[to].size()});//正向
g[to].push_back((node){from,0,(int)g[from].size()-1});//反向,g[from]已经加入新值,下标size-1
}
inline void fc(int s)//深度信息
{
for(int i=0;i<=n;i++)dep[i]=-1;
queue<int>q;//储存节点编号
dep[s]=0;
q.push(s);
while(!q.empty())
{
int u=q.front();q.pop();
for(auto v:g[u])
{
if(v.c>0&&dep[v.to]<0)//容量大于0且没被计算过
{
dep[v.to]=dep[u]+1;
q.push(v.to);
}
}
}
}
inline int dfs(int u,int t,int f)
{
if(u==t||!f) return f;
int ans=0;
for(int &i=pos[u];i<g[u].size();i++)//当前弧优化,重复经过同一个节点时,跳过已经跑满的边,巧妙地更新pos值实现
{
auto &x=g[u][i];//g[u][i]的信息要被修改
if(x.c>0&&dep[u]+1==dep[x.to])//有容量且层数相邻
{
int frz=dfs(x.to,t,min(f,x.c));
if(frz>0)
{
x.c-=frz;g[x.to][x.lp].c+=frz;
f-=frz;ans+=frz;
if(!f) break;//剪枝,现在找不到妹子,以后也找不到。
}
}
}
return ans;
}
inline ll dinic(int s,int t)
{
ll max_flow=0;
while(1)
{
fc(s);
if(dep[t]==-1)return max_flow;
for(int i=0;i<=n;i++)pos[i]=0;
max_flow+=dfs(s,t,inf);
}
}
inline void solve()
{
n=read();m=read();S=read();T=read();
for(int i=1;i<=m;i++)
{
int x,y,c;
x=read();y=read();c=read();
add(x,y,c);
}
write(dinic(S,T));
}
完整板子:
#ifdef ONLINE_JUDGE
#else
#define Qiu_Cheng
#endif
#include <bits/stdc++.h>
// #define int long long
using namespace std;
typedef long long ll;
const int N=205,mod=1e9+7,inf=INT_MAX;
// const int mod1=469762049,mod2=998244353,mod3=1004535809;
// const int G=3,Gi=332748118;
// const int M=mod1*mod2;
inline int read()
{
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){if(c=='-'){f=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c-'0');c=getchar();}
return x*f;
}
inline void write(ll x)
{
if(x<0){putchar('-');x=-x;}
if(x>9) write(x/10);
putchar(x%10+'0');
}
struct node{int to,c,lp;};
vector<node>g[N];
int dep[N],pos[N];
int n,m,S,T;
inline void add(int from,int to,int c)
{
g[from].push_back((node){to,c,(int)g[to].size()});
g[to].push_back((node){from,0,(int)g[from].size()-1});
}
inline void fc(int s)//深度信息
{
for(int i=0;i<=n;i++)dep[i]=-1;
queue<int>q;//储存节点编号
dep[s]=0;
q.push(s);
while(!q.empty())
{
int u=q.front();q.pop();
for(auto v:g[u])
{
if(v.c>0&&dep[v.to]<0)
{
dep[v.to]=dep[u]+1;
q.push(v.to);
}
}
}
}
inline int dfs(int u,int t,int f)
{
if(u==t||!f) return f;
int ans=0;
for(int &i=pos[u];i<g[u].size();i++)//当前弧优化
{
auto &x=g[u][i];//g[u][i]的信息要被修改
if(x.c>0&&dep[u]+1==dep[x.to])//有容量且层数相邻
{
int frz=dfs(x.to,t,min(f,x.c));
if(frz>0)
{
x.c-=frz;g[x.to][x.lp].c+=frz;
f-=frz;ans+=frz;
if(!f) break;//剪枝
}
}
}
return ans;
}
inline ll dinic(int s,int t)
{
ll max_flow=0;
while(1)
{
fc(s);
if(dep[t]==-1)return max_flow;
for(int i=0;i<=n;i++)pos[i]=0;
max_flow+=dfs(s,t,inf);
}
}
inline void solve()
{
n=read();m=read();S=read();T=read();
for(int i=1;i<=m;i++)
{
int x,y,c;
x=read();y=read();c=read();
add(x,y,c);
}
write(dinic(S,T));
}
signed main()
{
#ifdef Qiu_Cheng
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
// ios::sync_with_stdio(false);
//cin.tie(0); cout.tie(0);
// int QwQ;
// cin>>QwQ;
// while(QwQ--)solve();
solve();
return 0;
}
//12 825076913 0 173167432
// 6666 66666 666666
// 6 6 6 6 6
// 6 6 6666 6
// 6 6 6 6 6
// 6666 6 6 6666666
//g++ -O2 -std=c++14 -Wall "-Wl,--stack= 536870912 " cao.cpp -o cao.exe



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 终于写完轮子一部分:tcp代理 了,记录一下
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通
· 【硬核科普】Trae如何「偷看」你的代码?零基础破解AI编程运行原理