洛谷 P5854 【模板】笛卡尔树
洛谷P5854 【模板】笛卡尔树
摸鱼环节
【模板】笛卡尔树
题目描述
给定一个 \(1 \sim n\) 的排列 \(p\),构建其笛卡尔树。
即构建一棵二叉树,满足:
- 每个节点的编号满足二叉搜索树的性质。
- 节点 \(i\) 的权值为 \(p_i\),每个节点的权值满足小根堆的性质。
输入格式
第一行一个整数 \(n\)。
第二行一个排列 \(p_{1 \dots n}\)。
输出格式
设 \(l_i,r_i\) 分别表示节点 \(i\) 的左右儿子的编号(若不存在则为 \(0\))。
一行两个整数,分别表示 \(\operatorname{xor}_{i = 1}^n i \times (l_i + 1)\) 和 \(\operatorname{xor}_{i = 1}^n i \times (r_i + 1)\)。
样例 #1
样例输入 #1
5
4 1 3 2 5
样例输出 #1
19 21
提示
【样例解释】
| \(i\) | \(l_i\) | \(r_i\) |
|---|---|---|
| \(1\) | \(0\) | \(0\) |
| \(2\) | \(1\) | \(4\) |
| \(3\) | \(0\) | \(0\) |
| \(4\) | \(3\) | \(5\) |
| \(5\) | \(0\) | \(0\) |
【数据范围】
对于 \(30\%\) 的数据,\(n \le 10^3\)。
对于 \(60\%\) 的数据,\(n \le 10^5\)。
对于 \(80\%\) 的数据,\(n \le 10^6\)。
对于 \(90\%\) 的数据,\(n \le 5 \times 10^6\)。
对于 \(100\%\) 的数据,\(1 \le n \le 10^7\)。
首先,经过查阅大量资料(一篇),我也没发现笛卡尔树与笛卡尔的关系。
其次,没了。
正片开始
What is the 笛卡尔树?
笛卡尔树是一种二叉树,每一个节点由一个键值二元组 $(k,w) \(构成。要求\) k $满足二叉搜索树的性质,而 $w \(满足堆的性质。如果笛卡尔树的\) k,w $键值确定,且 $k \(互不相同,\)w $也互不相同,那么这棵笛卡尔树的结构是唯一的。如下图:

上面这棵笛卡尔树相当于把数组元素值当作键值 \(w\),而把数组下标当作键值$ k$。可以发现,这棵树的键值 $k \(满足二叉搜索树的性质,而键值\) w $满足小根堆的性质。同时根据二叉搜索树的性质,可以发现这种特殊的笛卡尔树满足一棵子树内的下标是一个连续区间。
竞赛中使用笛卡尔树时,常用数组下标作为二元组的键值$ k$。
--摘自OI-Wiki
thinking
该如何建一棵笛卡尔树呢?
显然,我们可以按下标顺序一个个插进一棵树里,而每次插入树的位置必然在这棵树的右链(右链:即从根节点一直往右子树走,经过的节点形成的链)的末端。
于是我们可以比较右链节点与当前节点\(u\)的\(w\),如果右链上的节点\(x\)满足\(w_{x} < w_{u}\),就把\(u\)接到\(x\)的右儿子上,把\(x\)原本的右子树接到\(u\)的左儿子上。如下图:
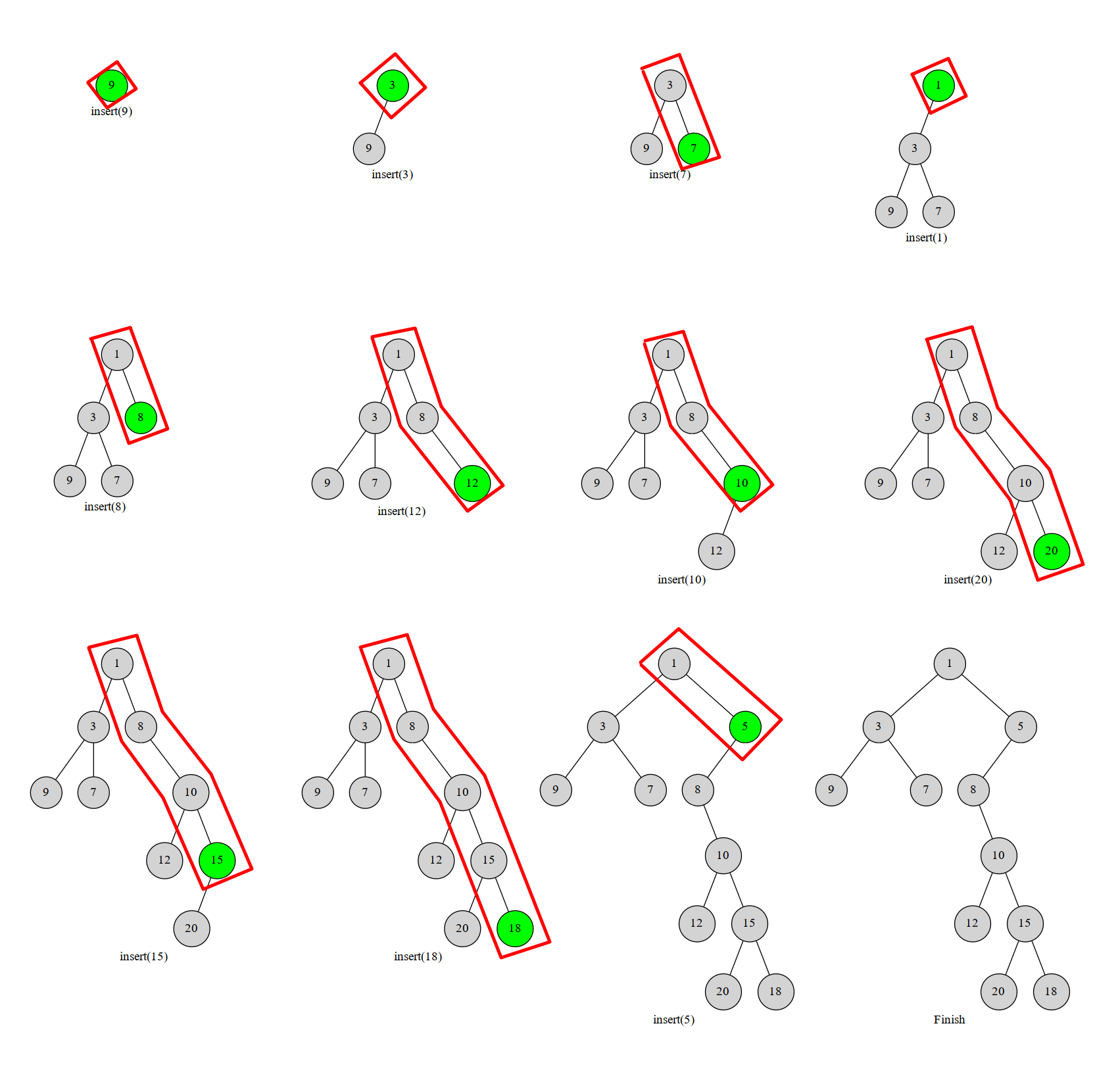
--摘自OI-Wiki
然后我们发现得到了一个\(O(n_{2})\)的算法,似乎有点劣。
考虑优化过程,每次我们需要从后往前找到第一个比插入数小的数,显然这个过程可以用单调栈维护。每个点进出栈一次,于是我们得到一个\(O(n)\)的算法。
code
- 科技版本
void build()//stack写法
{
stack<int>s;//stack储存的是下标
for(int i=1;i<=n;i++)
{
while(!s.empty()&&frz[s.top()].b>frz[i].b)//栈顶元素太大了,移接i的左儿子
{
l_son[i]=s.top();
s.pop();
}
if(!s.empty())r_son[s.top()]=i;//i挂在合法节点的右儿子
s.push(i);
}
}
- 手活版本
void build2()//手模stack写法,st数组储存的依然还是下标
{
int pos=0,top=0;//记录当前位置,与栈顶元素
for(int i=1;i<=n;i++)
{
pos=top;
while(pos&&frz[st[pos]].b>frz[i].b) pos--;//寻找合法节点
if(pos)r_son[st[pos]]=i;//有合法节点,i挂合法节点的右边
if(pos<top) l_son[i]=st[pos+1];//当pos<top时说明插入点在中间,将pos后一位挂在i的左儿子
st[++pos]=i;//i入栈
top=pos;//更新栈顶
}
}
- 注意事项
- 数组需要开到\(1e7\)。
- 如果爆了,尝试开\(long long\)(十年OI一场空,不开longlong见祖宗)。
完整代码
#ifdef ONLINE_JUDGE
#else
#define Qiu_Cheng
#endif
#include <bits/stdc++.h>
#define int long long
using namespace std;
// typedef long long ll;
const int N=1e7+50,M=1e5+5,mod=1e9+7;
const double pi=acos(-1);
int n;
struct node
{
int a,b;//编号,权值
}frz[N];
int r_son[N],l_son[N];
inline int read()
{
int x=0,f=1;
char c=getchar();
while(c<'0'||c>'9'){if(c=='-'){f=-1;}c=getchar();}
while(c>='0'&&c<='9'){x=(x<<3)+(x<<1)+(c-'0');c=getchar();}
return x*f;
}
inline void write(int x)
{
if(x<0){putchar('-');x=-x;}
if(x>9) write(x/10);
putchar(x%10+'0');
}
void build()//stack写法
{
stack<int>s;
for(int i=1;i<=n;i++)
{
while(!s.empty()&&frz[s.top()].b>frz[i].b)
{
l_son[i]=s.top();
s.pop();
}
if(!s.empty())r_son[s.top()]=i;
s.push(i);
}
}
int st[N];
void build2()//手模stack写法
{
int pos=0,top=0;
for(int i=1;i<=n;i++)
{
pos=top;
while(pos&&frz[st[pos]].b>frz[i].b) pos--;
if(pos)r_son[st[pos]]=i;
if(pos<top) l_son[i]=st[pos+1];
st[++pos]=i;
top=pos;
}
}
inline void solve()
{
n=read();
for(int i=1;i<=n;i++) frz[i].b=read(),frz[i].a=i;
build();
int l=0,r=0;
for(int i=1;i<=n;i++) l^=(1ll*i*(l_son[i]+1));
for(int i=1;i<=n;i++) r^=(1ll*i*(r_son[i]+1));
printf("%lld %lld\n",l,r);
}
signed main()
{
#ifdef Qiu_Cheng
freopen("1.in","r",stdin);
freopen("1.out","w",stdout);
#endif
ios::sync_with_stdio(false);
cin.tie(0);
cout.tie(0);
// int Tt;
// cin>>Tt;
// while(Tt--)solve();
solve();
return 0;
}
// 6666 66666 666666
// 6 6 6 6 6
// 6 6 6666 6
// 6 6 6 6 6
// 6666 6 6 6666666
//g++ -O2 -std=c++14 -Wall "-Wl,--stack= 536870912 " cao.cpp -o cao.exe
完结收工!!!!!

看完点赞,养成习惯
\(\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\Downarrow\)

