CodeTON Round 6 (Div. 1 + Div. 2, Rated, Prizes!)(A-D)

CodeTON Round 6 (Div. 1 + Div. 2, Rated, Prizes!)

A.让你找mex为k的n个数，这n个数从0-x，问n个数的和最大值是多少

先判断不行的。然后行的肯定有0-k-1，剩下还有就选x就行。

查看代码

#include<iostream>
using namespace std;
typedef long long ll;
void solve()
{
	int n,k,x;
	cin>>n>>k>>x;
	if(n<k||x<k-1)
	{
		cout<<-1<<'\n';
		return;
	}
	int ans=k*(k-1)/2;
	int lef=n-(k);
	if(x>k)ans+=lef*x;
	else ans+=lef*(k-1);
	cout<<ans<<'\n';
}
signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin>>t;
	while(t--)solve();
	return 0;
}

B.给n个元素数组a和m个元素数组b，每次你可以任选一个bj元素，让ai=ai|bj,若干次操作，问a数组的异或和最小和最大分别是多少。

我们把n分奇偶来看。

n是奇数的时候，我们会发现无论你操作几次，最后都相当于最后操作一次，那么最小值就是原序列的异或合，最大值再或上b数组或和即可

n是偶数的时候，a数组里最后是1的位，如果这一位b的或和也为1，那么在操作后这一位就能变成0，最小值就是a-(a&b)，最大值就是a

查看代码

 #include<iostream>
using namespace std;
void solve()
{
	int n,m,x=0,y=0,a,b;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		cin>>a;
		x^=a;
	}
	for(int i=1;i<=m;i++)
	{
		cin>>b;
		y|=b;
	}
	if(n%2)
		cout<<x<<' '<<(x|y)<<'\n';
	else
		cout<<(x-(x&y))<<' '<<x<<'\n';
}
signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin>>t;
	while(t--)solve();
	return 0;
}

C.给一个n个元素数组a，里面有k种数，构成n*n的方阵b，bij=min(a[i],a[j])。对于每一个i(1<=i<=k)问能把方阵里值为i包括起来的最小方阵的长宽之和是多少

对于a[i],如果它前面有a[j]>a[i]，那么相应的b[j][i]和b[i][j]都是a[i]，对于后面也是如此

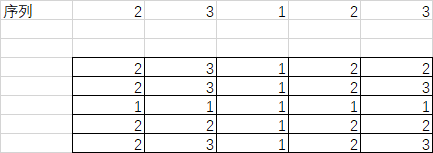
那么我们只需要找到在颜色i之前颜色大于i的最小下标作为l，在i之后颜色大于i的最大下标r，那么对于i的答案就是(r-l+1)*2

当我们依次从1到k枚举的时候有个性质。我们找到了a[l]>i，那么1-l-1中就必然没有大于i+1的。所以我们可以O(n)地求出答案

对于没有出现的元素。输出0即可

查看代码

 #include<iostream>
using namespace std;
int n,k,a[100005],ans[100005];
bool vis[100005];
void solve()
{
	for(int i=1;i<=k;i++)vis[i]=0;
	cin>>n>>k;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		vis[a[i]]=1;
	}
	int r=n,l=1;
	for(int i=1;i<=k;i++)
	{
		while(r>0&&a[r]<i)r--;
		ans[i]=r;
	}
	for(int i=1;i<=k;i++)
	{
		while(l<=n&&a[l]<i)l++;
		ans[i]-=l;
	}
	for(int i=1;i<=k;i++)
		cout<<(ans[i]+1)*2*vis[i]<<' ';
	cout<<"\n";
}
signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin>>t;
	while(t--)solve();
	return 0;
}

D.一开始有k的钱，有n个位置，在第i个位置购买1需要ci，买后1-i都会增加1，问买任意次任意物品后最大字典序是多少

对于ai,ai+1,ai<ai+1，我们先贪心地去买ai，然后再去买ai+1发现买不了，有可能最优解是少买几个ai，然后再买几个ai+1,我们该如何后悔呢？

假设最多买x个ai，然后最优解是买y个ai和z个ai+1，而x==y+z，如果y+z<x，那么不如全买x的字典序更大了。

我们怎么求的z呢？假设买ai前是k,到买ai+1的时候剩下k-y*ai,然后z=(k-y*ai)/(ai+1),买这两个的花费是y*ai+z*(ai+1)=y*ai+z*ai+z*(ai+1-ai)

可以换成x*ai+z*(ai+1-ai)，那么我们只要减去前面买的价格后再计算买，就实现所谓的后悔贪心了。

对于ai,ai+1,ai>ai+1，那么最优的肯定是买后面的，而这个位上的答案也是后面的小的。

所以我们可以把数组处理成它后面最小的，然后O(n)处理下数组即可

查看代码

 #include<iostream>
using namespace std;
int n,k,c[200005];
void solve()
{
	cin>>n;
	for(int i=1;i<=n;i++)cin>>c[i];
	cin>>k;
	for(int i=n-1;i>0;i--)c[i]=min(c[i],c[i+1]);
	int a=k;
	for(int i=1;i<=n;i++)
	{
		int add=c[i]-c[i-1];
		a=min(a,add?k/add:a);
		k-=add*a;
		cout<<a<<" \n"[i==n];
	}
}
signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin>>t;
	while(t--)solve();
	return 0;
}