Pinely Round 2 (Div. 1 + Div. 2)(A-E)

Dashboard - Pinely Round 2 (Div. 1 + Div. 2) - Codeforces

A.题意是一共有n个用户，当前有a个用户在线，然后有m个用户上/下线通知，问是否有一时刻所有用户都在线。

简单的模拟，按照+-统计最大的和n的关系，和上线用户数量的关系判断下就行。

当时代码有点小乱。

查看代码


#pragma GCC optimize(2)
#include<iostream>
using namespace std;
typedef long long ll;
void solve()
{
	int n,q,m;
	cin>>n>>q>>m;
	int add=0,sub=0,tmp=q,suc=q;
	for(int i=0;i<m;i++)
	{
		char c;
		cin>>c;
		if(c=='+')add++,tmp++;
		else sub++,tmp--;
		suc=max(suc,tmp);
	}
	if(suc==n)
	{
		cout<<"YES\n";
		return;
	}
	if(suc<n&&q+add<n)
	{
		cout<<"NO\n";
	}
	else cout<<"MAYBE\n";
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin>>t;
	while(t--)solve();
	return 0;
}

B。题意是给你一个(1-n)的某个排列，每次可以选择一个数，让小于它的数按照原来的相对位置排到它前面，大于它的按照原来的相对位置排在它后面，然后问最少多少次操作把序列变成1-n

最坏可能是n-1次(毕竟最后一个不用动嘛)。

我们想一种情况，如果x+1在x后面的话，我们动x+1的时候就把x,x+1有序化了，相当于少操作一次。

我们存一下每个数的下标，判断下它加1在不在后面即可

然后

查看代码

 #pragma GCC optimize(2)
#include<iostream>
#include<vector>
using namespace std;
typedef long long ll;
ll a[100005],b[100005],n;
void solve()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		b[a[i]]=i;
	}
	int ans=n-1;
	for(int i=1;i<n;i++)
		if(b[a[i]+1]>b[a[i]]&&a[i]<n)ans--;
	cout<<ans<<"\n";
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin>>t;
	while(t--)solve();
	return 0;
}

C.给一个大小为n的数组，里面是0-n缺了一个数。然后每次操作都把a[i]换成mex{a1....an}，问k次操作后数组变成什么样。

既然是0-n这n+1个数缺少的那个数，那么每次操作都会让第一个数变成缺的数，然后第二个等于原来的第一个，第三个等于原来的第二个。。。。直到最后一个变成原来的倒数第二个。

那么再执行n-1次，缺的那个数到了最后一位，再执行一次，发现回到了原来的数组。即n+1次循环。

我们先将k%(n+1)，统计下缺的数和剩下的k，那么n-k+1这一位的数会在k轮操作后消失，它后面的加上此时缺的数再加上它前面的构成k轮后的数列。

查看代码

 #pragma GCC optimize(2)
#include<iostream>
#include<vector>
using namespace std;
typedef long long ll;
int a[100005],b[100005],n,k;
void solve()
{
	cin>>n>>k;
	for(int i=0;i<=n;i++)b[i]=0;
	for(int i=1;i<=n;i++)
	{
		cin>>a[i];
		b[a[i]]=1;
	}
	k%=(n+1);
	if(k==0)
	{
		for(int i=1;i<=n;i++)
		cout<<a[i]<<' ';
		cout<<"\n";
		return;
	}
	int mex=0;
	for(int i=0;i<=n;i++)
	{
		if(b[i]==0)
		{
			mex=i;
			break;
		}
	}
	int ft=n-k+1;
	vector<int>ans;
	for(int i=ft+1;i<=n;i++)
	{
		ans.push_back(a[i]);
	}
	ans.push_back(mex);
	for(int i=1;i<ft;i++)ans.push_back(a[i]);
	for(auto x:ans)
	cout<<x<<' ';
	cout<<"\n";
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin>>t;
	while(t--)solve();
	return 0;
}

D.题意是给一个n*m的格子，然后有两种特殊的占两块的格子，横着的LR,竖着的U,D，现在要求在两块的格子上涂黑白两种颜色，同一块L,R颜色相异，同一块U,D颜色相异，问是否能让每一行每一列的两种颜色格子相等。

想了差不多一个小时，想过DP,DSU，最后是按照之前看的PYY大佬的E. Tick, Tock[带权并查集] - qbning - 博客园 (cnblogs.com)想到的思路，尽管用的不是并查集，但也是过了。

L,R横着放，对于一行的黑白两色的个数平衡不会影响，那么我们来找U,D的数目，如果这一行U,D的数目为奇数，那么肯定不行。如果为偶数，那么

可以两两标记下，它们相异，同时给对应的D也标记下。这样每一次标记只用找U就行，因为这一行的D已经在上一行里标记好了。

LR,按列也这样找就行

查看代码

#pragma GCC optimize(2)
#include<iostream>
using namespace std;
typedef long long ll;
char mp[505][505];
int f[505][505],g[505][505];
void solve()
{
	int n,m,fail=0;
	cin>>n>>m;
	for(int i=1;i<=n;i++)
	{
		int cnt=0;
		for(int j=1;j<=m;j++)
		{
			cin>>mp[i][j];
			if(mp[i][j]=='U'||mp[i][j]=='D')cnt++;
			f[i][j]=0;
			g[i][j]=0;
		}
		if(cnt%2)
			fail=1;
	}
	for(int i=1;i<=m;i++)
	{
		int cnt=0;
		for(int j=1;j<=n;j++)
			if(mp[j][i]=='L'||mp[j][i]=='R')cnt++;
		if(cnt%2)
			fail=1;
	}
	if(fail)
	{
		cout<<-1<<"\n";
		return;
	}
	for(int i=1;i<=n;i++)
	{
		int la=0;
		for(int j=1;j<=m;j++)
		{
			if(mp[i][j]=='U')
			{
				if(la)
				{
					f[i][j]=la;
					f[i][la]=j;
					f[i+1][j]=la;
					f[i+1][la]=j;
					la=0;
				}
				else la=j;
			}
		}
		if(la)
		{
			cout<<-1<<'\n';
			return;
		}
	}
	for(int i=1;i<=m;i++)
	{
		int la=0;
		for(int j=1;j<=n;j++)
		{
			if(mp[j][i]=='L')
			{
				if(la)
				{
					g[j][i]=la;
					g[la][i]=j;
					g[j][i+1]=la;
					g[la][i+1]=la;
					la=0;
				}
				else la=j;
			}
		}
		if(la)
		{
			cout<<-1<<'\n';
			return;
		}
	}
	char ans[505][505];
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
		{
			if(mp[i][j]=='.')
			{
				ans[i][j]='.';
			}
			else if(mp[i][j]=='L')
			{
				ans[i][j]='W';
				ans[g[i][j]][j]='B';
			}
			else if(mp[i][j]=='U')
			{
				ans[i][j]='W';
				ans[i][f[i][j]]='B';
			}
			else if(mp[i][j]=='R')
			{
				ans[g[i][j]][j]=ans[i][j-1];
				if(ans[i][j-1]=='W')
					ans[i][j]='B';
				else
					ans[i][j]='W';
			}
			else if(mp[i][j]=='D')
			{
				ans[i][f[i][j]]=ans[i-1][j];
				if(ans[i-1][j]=='B')
					ans[i][j]='W';
				else ans[i][j]='B';
			}
		}
	}
	for(int i=1;i<=n;i++)
	{
		for(int j=1;j<=m;j++)
			cout<<ans[i][j];
		cout<<'\n';
	}
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin>>t;
	while(t--)solve();
	return 0;
}

有n个任务，m种依赖关系，每天有k小时，然后每个任务可以前置依赖完成后可以在每天的第hi小时完成，同时可以完成hi相同的任意数目的任务，问怎么安排任务顺序，来使得开始完成任务到完成最后的任务持续时间最短。

首先需要一个拓扑排序。接下来我们看下安排任务是怎么影响答案的。

5 0 1000
8 800 555 35 35

这个样例，无任何依赖，如果我们按照从小到大排序，完成总时长为800-8=792

在样例解释里，最佳方案应该是先完成555->800->第二天8->35，总时长为35+1000-555=480

就是说在没有依赖关系的时候，如果延后一天，第一天做比原来第一个任务hi更大的任务可能有更优解

然后我接下来一个小时在琢磨正着怎么模拟这个过程，猜了一个同一层的回想这个样例一样，但最后发现似乎只有无依赖项才会有这个样例这样的性质，最后也寄了。赛后看jiangly大佬的代码。

我们先求以当前点开始到与当前点有关系的最后一个任务结束用多长时间。这个可以从后往前来，用dp[i]记录下。如果一个点i有两个依赖x,y，那么它这两个依赖都会被dp[i]更新下。dp[x]=max(dp[x],dp[i]+(h[i]-h[x]+k)%k);

如果我们单纯去比较dp[i]的话没有意义，因为无法保证完成所有任务。

设t[i]=dp[i]+h[i]是以i为第一个任务时，与当前点有关系的最后一个任务完成时的结束时间。

因为没有依赖关系时同一段时间可以做无限多的任务，所以最大的t[i]就是所有任务最后一个任务完成时的时间。

对于这个样例来说，t={8,35,35,555,800}.最大的800，如果按照顺序的话，第一个完成的应该是8,那么此时答案是800-8。

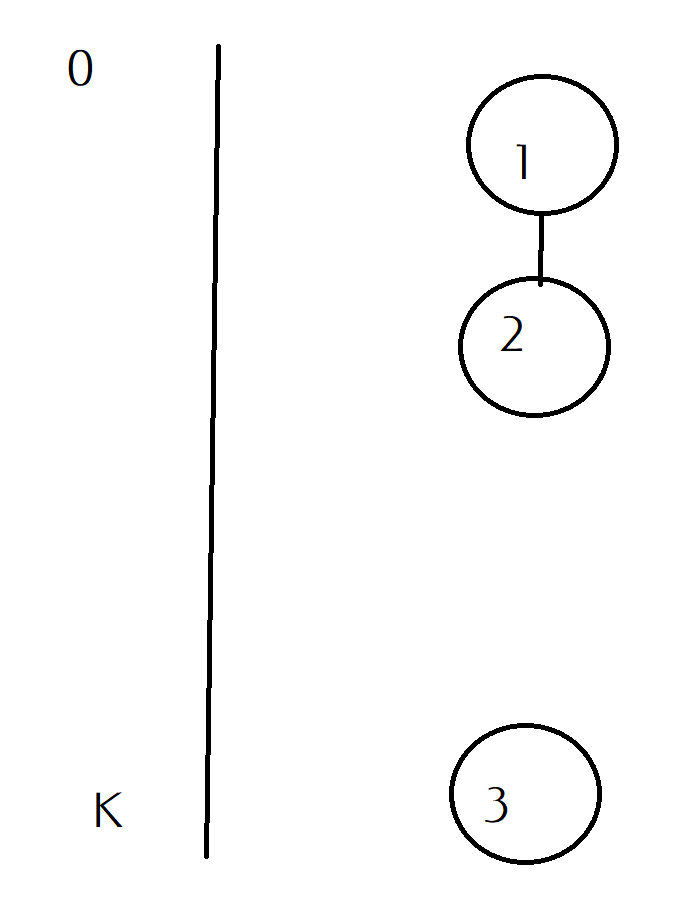
考虑一个如上图那样的情况，t[3]>t[1]>t[2],h[1]<h[2]<h[3]

按照顺序来的话是t[3]-h[1]，最优的是t[1]+k-h[3]

如果我们延后一个2而不去延后1，对答案是没有用的，因为这样增加了时间而没有延后开始任务的时间。所以，我们只能延后无依赖项的某个任务，然后把另一个无依赖项的任务安排在它前面可能会获得更短时间。

换言之，如果我们延后一个有依赖点，并不会改变此时第一个完成的任务，此时带来的结果>=之前的ans

不延后时候最后一个任务的完成时间是max_t=max(t[i]);

将一个无依赖点延后一天得到的结束时间是t[i]+k,如果t[i]+k大于max_t那么说明可以完成这些任务，

就样例8,35,35,555,800来看。我们把i及之前的放到第二天那么此时第一个完成的任务就是i+1.

所以我们可以对无依赖点进行排序，然后不断尝试把第i个放到第二天，i+1放到第一次，如果此时的最晚时间还能完成任务就减一下此时第一次的任务更新答案即可。

查看代码

 #pragma GCC optimize(2)
#include<iostream>
#include<vector>
#include<algorithm>
using namespace std;
typedef long long ll;
vector<ll>a[200005];
ll h[200005],b[200005],t[200005];
void solve()
{
	int n,m,k,x,y,last=0,ans=1e18;
	vector<ll>p,q;
	cin>>n>>m>>k;
	for(int i=1;i<=n;i++)
	{
		cin>>h[i];
		a[i].clear();
		b[i]=0;
		t[i]=0;
	}
	for(int i=1;i<=m;i++)
	{
		cin>>x>>y;
		a[x].push_back(y);
		b[y]++;
	}
	for(int i=1;i<=n;i++)
	{
		if(b[i]==0)
		q.push_back(i);
	}
	p=q;//存无依赖点
	for(int i=0;i<n;i++)
	{
		int x=q[i];
		for(auto y:a[x])
		{
			if(--b[y]==0)
			q.push_back(y);//存拓扑序
		}
	}
	for(int i=n-1;i>=0;i--)//倒序来更新
	{
		int x=q[i];
		for(auto y:a[x])
			t[x]=max(t[x],t[y]+(h[y]-h[x]+k)%k);
	}
	for(auto x:p)
	{
		t[x]+=h[x];
		last=max(t[x],last);
	}
	sort(p.begin(),p.end(),[](int x,int y)->bool{return h[x]<h[y];});
	for(auto x:p)
	{
		ans=min(ans,last-h[x]);
		last=max(last,t[x]+k);
	}
	cout<<ans<<'\n';
}
int main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin>>t;
	while(t--)solve();
	return 0;
}

突然发现P1113 杂务可以用E的思路来做，而这个题只是个普及题。。

AC代码

 #include<iostream>
#include<vector>
using namespace std;
typedef long long ll;
ll n,m,x,y;
ll t[10005],d[10005],dp[10005];
vector<int>a[10005];
signed main()
{
	cin>>n;
	for(int i=1;i<=n;i++)
	{
		cin>>x>>t[x]>>y;
		while(y)
		{
			a[y].push_back(x);
			d[x]++;
			cin>>y;
		}
	}
	vector<int>q;
	for(int i=1;i<=n;i++)
	{
		if(d[i]==0)
			q.push_back(i);
	}
	for(int i=0;i<n;i++)
	{
		int x=q[i];
		for(auto y:a[x])
		{
			if(--d[y]==0)
			q.push_back(y);
		}
	}
	for(int i=n-1;i>=0;i--)
	{
		int x=q[i];
		dp[x]=t[x];
		for(auto y:a[x])
		{
			dp[x]=max(dp[x],dp[y]+t[x]);
		}

	}
	ll ans=0;
	for(int i=1;i<=n;i++)ans=max(ans,dp[i]);
	cout<<ans;
	return 0;
}

总结，E题的bfs拓扑序应用范围应该会很广

posted @ 2023-08-31 02:10 qbning 阅读(113) 评论(0) 编辑收藏举报

刷新页面返回顶部

qbning

Pinely Round 2 (Div. 1 + Div. 2)(A-E)

公告