Codeforces Round 887 (Div. 2) D.Imbalanced Arrays

Problem - D - Codeforces

题目规定了一种“平衡数组”，数组中的任意一个数绝对值小于等于n且不等于零，任意两个数的和不为0，给n个数a[i]，分别表示位于i的数可以与a[i]个数(包括它自己)相加为正。

现在给出n和a数组，要求构造平衡数组，不能构造的话输出-1

我们不难得出以下结论

如果a[i]>a[j]，b[j]+b[k]>0，那么一定有b[i]+b[k]>0，对所有k(b[j]+b[k]>0的)来说，b[k]+b[i]>0；又因为a[i]>a[j]，那么就是说存在至少一个b[l],使得b[i]+b[l]>0同时b[j]+b[l]<0，所以综上b[i]>b[j]。即a[i]>a[j]则b[i]>b[j]。

为方便填数，我们不妨输入时保存好a数组的下标，然后按照a数组的大小升序排列。

按照下标如下表

1

l

.....

r

n

任选一个i，我们来分情况进行考虑。

1. 如果要填的数大于0，那么这个数和它本身以及后面的所有数相加都会大于0，也就说a[i]>=(n-r+1)

   那它和它前面多少数相加还大于0呢？

   我们设它一直到x，相加都是大于0的。如图

   

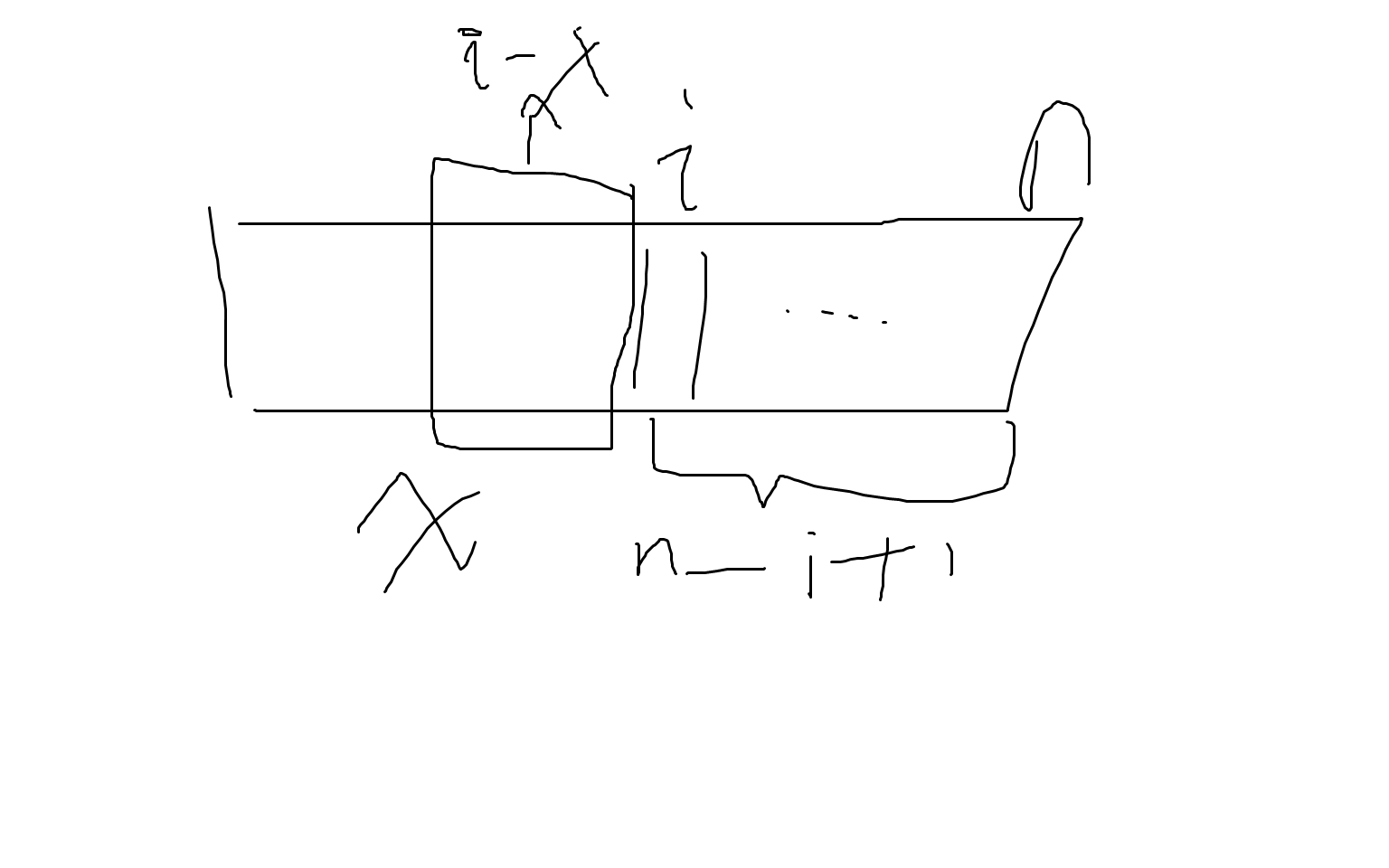
   此时，(i-x)+(n-i+1)=a[i],我们可以得到x=n-a[i]+1，也就是说，对于b[i]>0，它最多能和第n-a[i]+1个数相加大于0，而与n-a[i]+1之前的数相加小于0。

2.  
   1. 如果要填的数小于0，那么它和它前面的所有数相加都不会大于0，它只能从最大的数往前找的若干数的和大于0，如图

      此时，b[n],b[n-1],,,,b[x]和b[i]相加都大于0，那么n-x+1=a[i],x=n-a[i]+1.也就是说，对于b[i]<0，它和第n-a[i]+1到n的数相加大于0,而与1到 n-a[i]之间的数的和小于0

对于样例 1，4，3，4,排序后是 1,3,4,4  

因为涉及到±两种符号，而且最小的数可能会为负值，我们不妨设l=1,r=n，使l用来填入负值，r用来填入正值

l=1,r=4时,n-a[r]+1=1,意思是它此时和a[1]的和大于0，所以它的绝对值大于a[1]的绝对值，填入4

l=1,r=3时,n-a[r]+1=1,同r=4，此时可以填入4或3

l=1,r=2时,n-a[r]+1=2,因为2>1==1说明b[l]的绝对值是大于b[2]的，我们先填b[l]

l=1,r=2时,n-a[i]+1=1,如果b[l]>0，那么a[i]至少与1-4的数相加大于0，那么b[l]<0，接着b[1]和n-a[i]+1=1到4之间的数的和为正的，那么a[1]应该等于4，与a[1]=1矛盾，所以不存在解

所以综上，我们的思路分别设置l=1,r=n用来填负值和正值，设置now=n来决定具体的数值，在这一轮中，如果b[r]+b[l]>0，也就是b[r]正好是到l相加的数大于0，即n-a[r]+1==l,那么说明abs(b[r])>abs(b[l])，所以b[a[r].pos]=now,然后r--，now--,如果b[r]+b[l]<0，也就是正好b[l]+b[r]>0,即n-a[l]==r.

当两者都不符合时，说明此处正负数都没法填写，无法构造对应序列。

 

查看代码

#pragma GCC optimize(2)
#pragma GCC optimize(3)
#include <algorithm>
#include <cstring>
#include <iostream>
#define int long long
#define fir first
#define sec second
using namespace std;
pair<int, int> a[200005];
int b[200005];
void solve() {
  int n;
  cin >> n;
  for (int i = 1; i <= n; i++) {
    cin >> a[i].fir;
    a[i].sec = i;
  }
  if (n == 1) {
    if (a[1].fir == 1)
      cout << "YES\n1\n";
    else if (a[1].fir == 0)
      cout << "YES\n-1\n";
    else
      cout << "No" << '\n';
    return;
  }
  memset(b, 0, sizeof(b));
  sort(a + 1, a + 1 + n);
  int l = 1, r = n, now = n;
  while (l <= r) {
    if (n - a[r].fir + 1 == l) {
      b[a[r--].sec] = now--;
      continue;
    }
    if (n - a[l].fir == r) {
      b[a[l++].sec] = -(now--);
      continue;
    }
    cout << "NO\n";
    return;
  }
  cout << "YES\n";
  for (int i = 1; i <= n; i++) cout << b[i] << ' ';
  cout << "\n";
}
signed main() {
  int t;
  cin >> t;
  while (t--) {
    solve();
  }
  return 0;
}