近段时间数据结构的上机作业
上机作业1:一元n次多项式的存储和处理
一元n次多项式定义如下: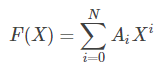
其中为实数,i为不小于0的整数。定义一元n次多项式操作包括:
(1)输入各个系数和指数i,创建一个多项式;
(2) 输出多项式:将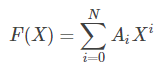 一元n次多项式输出为:F(X)=X^n+...+X+
一元n次多项式输出为:F(X)=X^n+...+X+
(3) 两个多项式相加:输入两个多项式,求出并输出两个多项式的和;
(4) 两个多项式相减:输入两个多项式,求出并输出两个多项式的差;
(5) 两个多项式相乘:输入两个多项式,求出并输出两个多项式的积;
(6) 求函数值:输入X,求出并输出一元n次多项式的值。
要求使用链表实现上述一元n次多项式的存储和操作处理。
输入格式:
有两个一元n次多项式,分别为:
f(X)=+ +
g(X)=-
其中系数为实数,指数取不小于0的整数,求x=10时f(x)的值。则输入分为3行,第1行为第一个一元n次多项式,第1个一元n次多项式按照第1项系数,指数 第2项系数,指数 .... 的格式输入,系数和指数以“,”分割,各项的系数和指数之间以空格分割,输入一元n次多项式不要求由高次项到低次项排列,最后以 0,0(即系数=0,指数=0)表示结束,输入多项式可以为空。第2行为第二个一元n次多项式,输入格式与第一个一元n次多项式相同。第3行为X的值。对上面的两个一元n次多项式:
输入样例:
3,2 1,1 1,0 0,0
-2,2 -1,1 -1,0 0,0
10输出格式:
输出分为以下几行:第1行输出第1个一元n次多项式,第2行输出第2个一元n次多项式,第3行输出两个一元n次多项式的和,第4行输出两个一元n次多项式的差,第5行输出两个一元n次多项式的乘积,第6行输出第1个一元n次多项式带入X后求出的值。输出要求一元n次多项式的高次项在前,低次项在后,实数保留小数点后面1位数,一元多项式为空时输出为空,即:若g(x)输入为空,输为g(x)=。对上面2个一元n次多项式的输出为:
输出样例:
f(x)=3.0X^2+X+1.0
g(x)=-2.0X^2-X-1.0
f(x)+g(x)=X^2
f(x)-g(x)=5.0X^2+2.0X+2.0
f(x)*g(x)=-6.0X^4-5.0X^3-6.0X^2-2.0X-1.0
f(10.0)=311.0//链表加调试,然后.....vs yyds!!!能告诉我哪里又忘记判NULL了
查看代码
#include<iostream>
#include<cmath>
#include<cstdlib>
#include<algorithm>
#define eps 1e-6
using namespace std;
struct node
{
double k;
int i;
node()
{
k = 0;
i = 0;
}
node* head;
node* next;
};
node* h1, * h2, * t1, * t2, * p1, * p2;
void output(node* a, node* b)
{
if (a == b)
{
puts("");
return;
}
node* p = a->next;
if (fabs(p->k) != 1 && p->i != 0 || p->i == 0)
printf("%.1f", p->k);
if (p->i != 0)
{
if (fabs(p->i) != 1)
{
cout << "X^" << p->i;
}
else
{
if (p->k == -1)
cout << '-';
cout << 'X';
}
}
p = p->next;
if (p == NULL)
{
puts("");
return;
}
while (p->next != NULL)
{
if (p->k > 0)
cout << "+";
if (p->k == -1)cout << '-';
if (fabs(p->k) != 1)
printf("%.1f", p->k);
if (p->i != 0)
{
if (fabs(p->i) != 1)
cout << "X^" << p->i;
else
cout << "X";
}
else
printf("%.1f", p->k);
p = p->next;
}
if (p == NULL)
{
puts("");
return;
}
if (p->k > 0)
cout << "+";
printf("%.1f", p->k);
if (p->i != 0)
{
if (fabs(p->i) != 1)
cout << "X^" << p->i;
else
cout << "X";
}
puts("");
}
void sort(node** h, node** t)
{
if (*h == *t)
{
return;
}
bool flag = 1;
while (flag)
{
flag = 0;
node* i = (*h)->next;
while (i != (*t))
{
if ((i->i) < (i->next->i))
{
swap(i->i, i->next->i);
swap(i->k, i->next->k);
flag = 1;
}
i = i->next;
}
}
}
void push(node** p, int i, double k)
{
node* o = new node;
o->head = (*p);
o->next = NULL;
o->i = i;
o->k = k;
(*p)->next = o;
*p = o;
}
void pre(node** h, node** t)
{
if (*h == *t)return;
sort(h, t);
node* h1, * t1;
h1 = new node;
t1 = h1;
node* p = (*h)->next;
while (p != *t || p == *t)
{
int q = p->i;
double cc = 0;
while (p->i == q && (p != *t || p == *t))
{
//cout<<"q=="<<q<<" p->i=="<<p->i<<endl;
cc += p->k;
if (p == *t || p == NULL)break;
p = p->next;
}
//cout<<"q=="<<q<<" cc=="<<cc<<endl;
if (cc)
push(&t1, q, cc);
if (p == *t && p->i == q)break;
if (p == NULL)break;
}
*h = h1;
*t = t1;
}
void add(node* a, node* a2, node* b, node* b2, char opera)
{
int flag = 1;
if (opera == '-')flag = -1;
node* c, * d, * p, * pp1 = a, * pp2 = b;
c = new node;
d = c;
if (a != a2)
pp1 = a->next;
if (b != b2)
pp2 = b->next;
while (pp1 != a2)
{
int i = pp1->i;
double k = pp1->k;
push(&d, i, k);
pp1 = pp1->next;
}
push(&d, a2->i, a2->k);
while (pp2 != b2)
{
int i = pp2->i;
double k = pp2->k;
push(&d, i, k * flag);
pp2 = pp2->next;
}
push(&d, b2->i, flag * (b2->k));
sort(&c, &d);
pre(&c, &d);
output(c, d);
}
void mul(node* a, node* a2, node* b, node* b2)
{
if (a == a2 || b == b2)
{
puts("");
return;
}
node* h, * t, * h2, * t2;
h = new node;
h2 = new node;
t2 = h2;
h->next = NULL;
t = h;
node* p = NULL, * pp1 = NULL, * pp2 = NULL;
pp1 = a->next;
while (pp1 != a2 || pp1 == a2)
{
double x = pp1->k;
int i = pp1->i;
pp2 = b->next;
while (pp2 != b2 || pp2 == b2)
{
double y = pp2->k;
int j = pp2->i;
push(&t, i + j, x * y);
if (pp2 == b2)break;
pp2 = pp2->next;
}
if (pp1 == a2)break;
pp1 = pp1->next;
}
if (t == h)
{
puts("");
return;
}
sort(&h, &t);
p = h->next;
while (p != t || p == t)
{
int q = p->i;
double cc = 0;
while (p->i == q && (p != t || p == t))
{
cc += p->k;
p = p->next;
if (p == t || p == NULL)break;
}
push(&t2, q, cc);
if (p == t && p->i == q)break;
if (p == NULL)break;
}
if (h2 == t2)
{
puts("");
return;
}
sort(&h2, &t2);
output(h2, t2);
}
void cal(double x, node* a, node* a2)
{
double ans = 0;
if (a == a2)return;
node* t = a->next;
while (t != a2)
{
ans = ans + t->k * pow(x, t->i);
t = t->next;
}
ans = ans + (a2->k * pow(x, a2->i));
printf("f(%.1f)=%.1f", x, ans);
}
int main()
{
int b;
double a;
char c;
h1 = new node;
h2 = new node;
t1 = h1;
t2 = h2;
cin >> a >> c >> b;
while (a != 0 || b != 0)
{
push(&t1, b, a);
cin >> a >> c >> b;
}
sort(&h1, &t1);
pre(&h1, &t1);
cout << "f(x)=";
output(h1, t1);
cin >> a >> c >> b;
while (a != 0 || b != 0)
{
push(&t2, b, a);
cin >> a >> c >> b;
}
sort(&h2, &t2);
pre(&h2, &t2);
cout << "g(x)=";
output(h2, t2);
cout << "f(x)+g(x)=";
add(h1, t1, h2, t2, '+');
cout << "f(x)-g(x)=";
add(h1, t1, h2, t2, '-');
cout << "f(x)*g(x)=";
mul(h1, t1, h2, t2);
double x;
cin >> x;
cal(x, h1, t1);
return 0;
}
上机作业2:二叉树的建立和遍历
对如下二叉树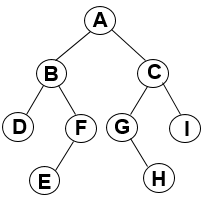
已知二叉树的完全前序序列可以唯一确定一棵二叉树。现给出二叉树的完全前序序列,使用C或C++编写算法完成:
(1) 以二叉链表为存储结构,建立二叉树;
(2) 编写先序遍历算法,输出先序遍历序列;
(3) 编写中序遍历算法,输出中序遍历序列;
(4) 编写后序遍历算法,输出后序遍历序列;
(5) 编写层序遍历算法,输出层序遍历序列,要求按层输出,每层输出一行;
(6) 编写算法,计算并输出二叉树的叶子数;
(7) 编写算法,计算并输出二叉树的高度。
输入格式:
二叉树数据元素为单个字符且各不相同,取值范围为A~Z,a~z,二叉树不为空。输入数据分为2行,第1行为二叉树完全前序序列字符(包括#)个数,第2行为二叉树的完全前序序列。例如,上面二叉树的输入为:ABD##FE###CG#H##I##,其中#代表为空的位置。
输出格式:
输出分为以下几行:
第1行为先序遍历序列
第2行为中序遍历序列
第3行为后序遍历序列
第4行及后面紧跟的几行为层序遍历序列,有几层输出几行
紧跟后面行输出叶子节点数(整数)
最后1行输出树的高度(整数)
输入样例:
以上面的二叉树为例,输入为:
19
ABD##FE###CG#H##I##输出样例:
对于上面的输入,输出为:
preorder traversal:ABDFECGHI
inorder traversal:DBEFAGHCI
postorder traversal:DEFBHGICA
level traversal:
A
BC
DFGI
EH
4
4其中"preorder traversal:"、"inorder traversal:"、"postorder traversal:"、"level traversal:"为先序、中序、后序序列的提示信息。
查看代码
#include<iostream>
#include<queue>
using namespace std;
typedef struct tree
{
char c;
tree *lson,*rson;
int lev;
tree()
{
lson=NULL;
rson=NULL;
lev=0;
}
}*btree;
tree *r;
int depth=0,leaf=0;
void build(btree &P,int k)
{
char c;
cin>>c;
if(c=='#')
{
P=NULL;
return;
}
P=new tree;
P->c=c;
P->lev=k;
depth=max(depth,k);
build(P->lson,k+1);
build(P->rson,k+1);
}
void pre(btree P)
{
if(P==NULL)return;
cout<<P->c;
pre(P->lson);
pre(P->rson);
}
void mid(btree P)
{
if(P==NULL)return;
mid(P->lson);
cout<<P->c;
mid(P->rson);
}
void post(btree P)
{
if(P==NULL)return;
post(P->lson);
post(P->rson);
cout<<P->c;
}
void level(btree P)
{
queue<btree>q;
if(P!=NULL)q.push(P);
int dep=-1;
while(q.size())
{
btree a=q.front();
if(a->lson==NULL&&a->rson==NULL)leaf++;
if(dep<a->lev)
{
puts("");
dep=a->lev;
}
cout<<a->c;
q.pop();
if(a->lson)
q.push(a->lson);
if(a->rson)
q.push(a->rson);
}
puts("");
}
int main()
{
r=new tree;
int n;
cin>>n;
build(r,0);
cout<<"preorder traversal:";
pre(r);
cout<<"\ninorder traversal:";
mid(r);
cout<<"\npostorder traversal:";
post(r);
cout<<"\nlevel traversal:";
level(r);
cout<<leaf<<endl<<depth+1<<endl;
return 0;
}-------------------------------------------
个性签名:曾经的我们空有一颗望海的心,却从没为前往大海做过真正的努力
如果觉得这篇文章对你有小小的帮助的话,记得在右下角点个“推荐”哦,博主在此感谢!



