分形之城

分形之城

问题 J: 分形之城
时间限制: 1 Sec 内存限制: 128 MB

题目描述
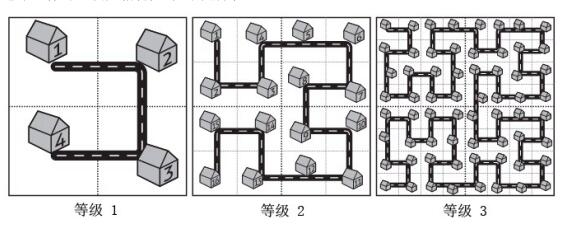
城市的规划在城市建设中是个大问题。不幸的是，很多城市在开始建设的时候并没有很好的规划，城市规模扩大之后规划不合理的问题就开始显现。而这座名为 Fractal 的城市设想了这样的一个规划方案，如下图所示：

当城区规模扩大之后，Fractal 的解决方案是把和原来城区结构一样的区域按照图中的方式建设在城市周围，提升城市的等级。对于任意等级的城市，我们把正方形街区从左上角开始按照道路标号。虽然这个方案很烂，Fractal 规划部门的人员还是想知道，如果城市发展到了等级 N，编号为 A 和 B 的两个街区的直线距离是多少。街区的距离指的是街区的中心点之间的距离，每个街区都是边长为 10 米的正方形。
输入
输入包含多组测试数据，第一行有一个整数 T 表示测试数据的数目。
每组测试数据包含一行三个整数 N, A, B，表示城市等级以及两个街区的编号。
输出
对于每组测试数据，在单独的一行内输出答案，四舍五入到整数。
样例输入
3
1 1 2
2 16 1
3 4 33
样例输出
10
30
50
提示
对于 30% 的数据，N≤5，T≤10。
对于 100% 的数据，N≤31，1≤A,B≤22N 。T≤1000。

这个题对我来说还是有点难..

为方便起见,将各个城市的编号减1
观察我们可以发现,等级每增一级,都有如下规律:

第n级每条边有2^n个房子记为len
左上角:上一级顺时针转90°,关于y轴翻转
坐标变换:(y,x)
右上角:保持原状
坐标变换:(x,y+len/2)
右下角:保持原状
坐标变换:(x+len,y+len)
左下角:上一级逆时针转90°,关于y轴翻转
坐标变换:(2 * len-y-1,len-x-1)

我们需要递归确定某个房子在某n-----等级中位于哪个角就可以计算出坐标啦

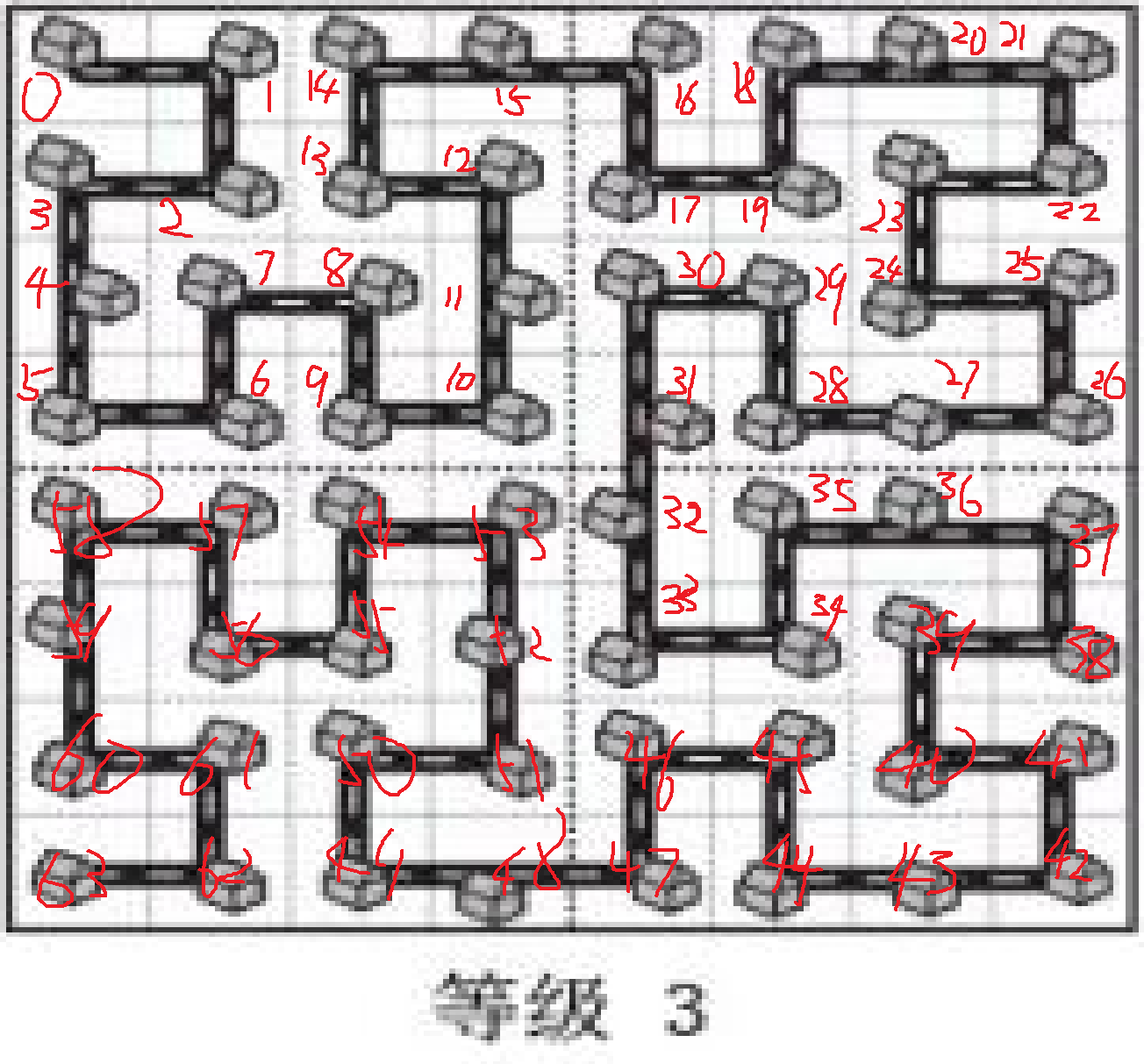
如果我们要定位23(实际是24)号的房屋,我们可以算出上一级房屋共有2^(2 * 2)=16
23 / 16 = 1所以23号所在的上一级房屋在左上角23%16=7

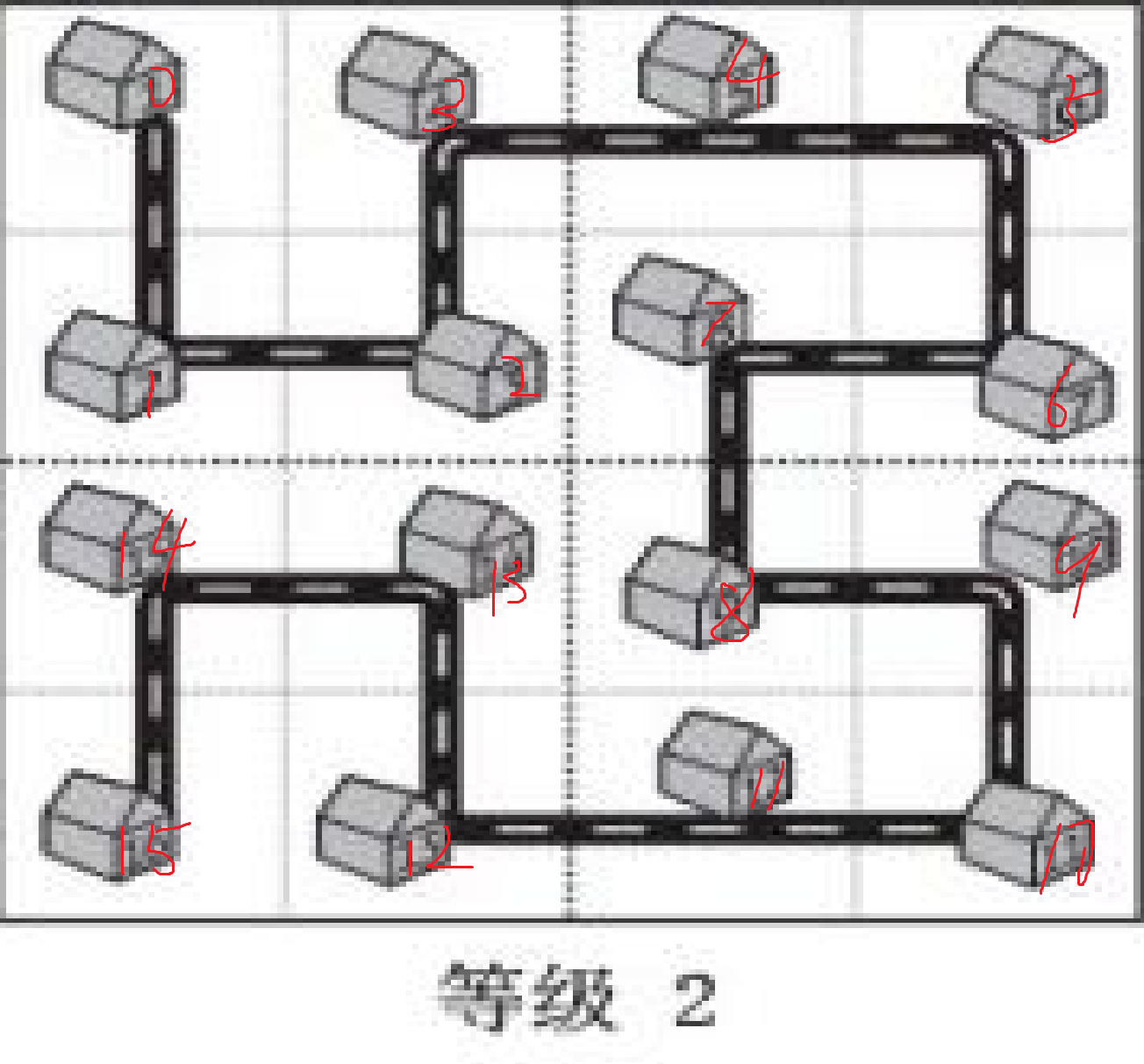
等级二中,上一级的房屋共有2^(2 * 1)=4
7/4=1所以23在右上角7%4=3

我们继续下去

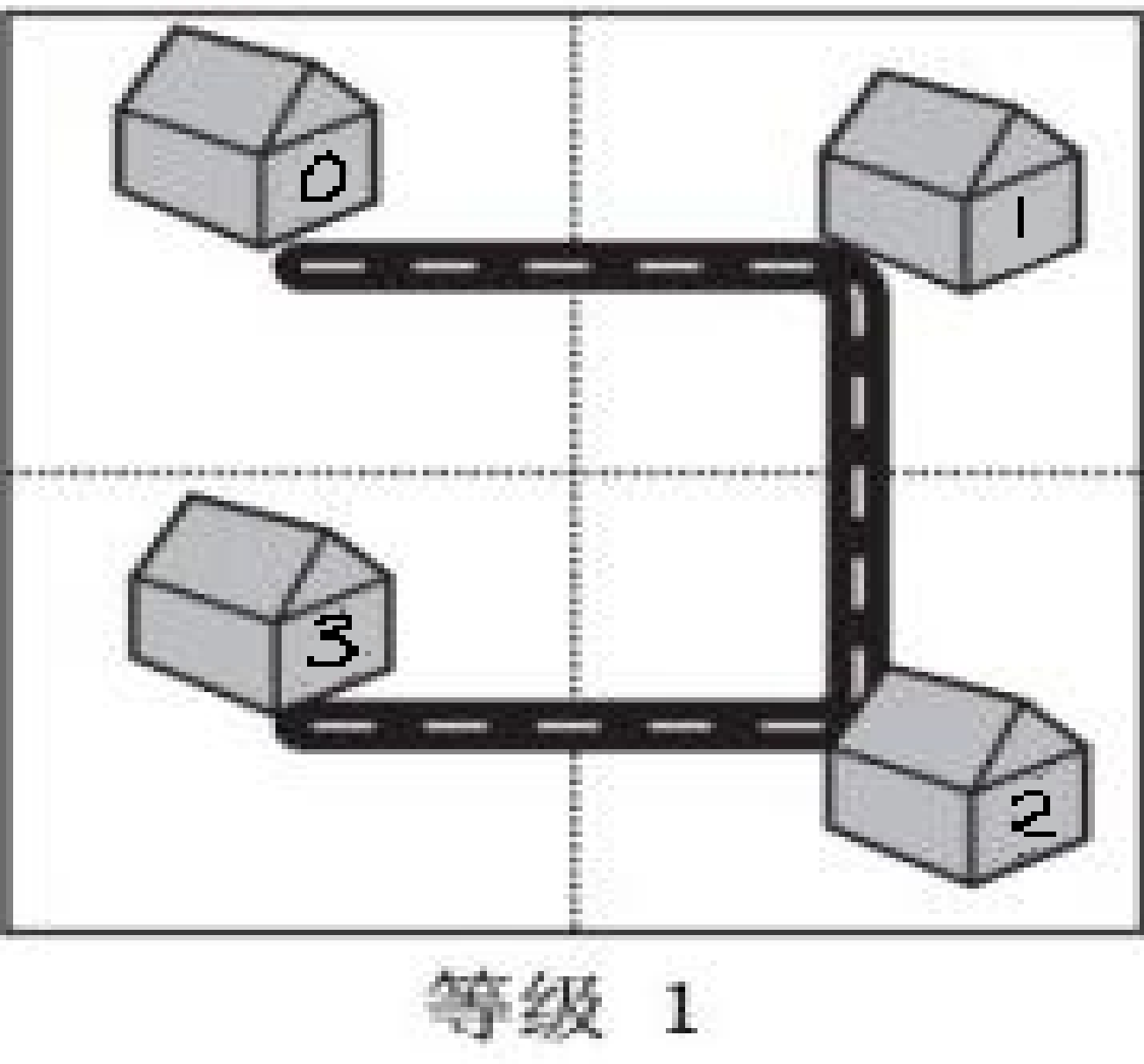
这里已经没有上一级分形之城了,2^(2 * 0) = 1
3/1=3 3%1=0
我们得知在左下角
接着模数为零到达递归的返回点
返回(0,0);

由于上一层(等级一)商为3
这一层一半边长为2^(1-1)=1
返回(2^1-0-1,20-0-1)即(1,0)

到达等级二
商为1
这一层一半边长为2^(2-1)=2
返回(1,0+2)=(1,2)

到达等级三
商为1
这一层半边长为2^(3-1)=4
返回(1,6)
得到23号的坐标为(1,6)

下面是代码

#include<iostream>
#include<cmath>
using namespace std;


typedef long long LL;
typedef pair<LL,LL>PLL;

PLL calc(LL N, LL M)
{
	if(N==0)return{0,0};
	
	LL cnt=1ll<<(2*N-2);
	LL len=1ll<<(N-1);
	 
	PLL p=calc(N-1,M%cnt) ;
	LL x=p.first ,y=p.second ;
	int Z=M/cnt;//
	if(Z==0)return{y,x};
	if(Z==1)return{x,y+len};
	if(Z==2)return{x+len,y+len};
	return {2*len-y-1,len-x-1};
}
int main()
{
	int t;
	cin>>t;
	while(t--)
	{
		LL N, A, B;
		cin>>N>>A>>B;
		PLL a=calc(N,A-1);
		PLL b=calc(N,B-1);
		LL c=pow(a.first -b.first ,2)+pow(a.second -b.second ,2);
		printf("%.0f\n",sqrt(c)*10); 
	}
	return 0;
}