个人项目作业-求交点个数

项目	内容
这个作业属于哪个课程	2020计算机学院软件工程(罗杰 任健)
这个作业的要求在哪里	个人项目作业
教学班级	005
GitHub地址	BUAASE-HW1-IntersectProject

一.PSP表格填写

• 在开始实现程序之前，在下述 PSP 表格记录下你估计将在程序的各个模块的开发上耗费的时间。
• 在你实现完程序之后，在下述 PSP 表格记录下你在程序的各个模块上实际花费的时间。

PSP2.1	Personal Software Process Stages	预估耗时（分钟）	实际耗时（分钟）
Planning	计划
· Estimate	· 估计这个任务需要多少时间	395	450
Development	开发
· Analysis	· 需求分析 (包括学习新技术)	60	120
· Design Spec	· 生成设计文档	20	10
· Design Review	· 设计复审 (和同事审核设计文档)	10	0
· Coding Standard	· 代码规范 (为目前的开发制定合适的规范)	20	0
· Design	· 具体设计	30	30
· Coding	· 具体编码	90	60
· Code Review	· 代码复审	30	60
· Test	· 测试（自我测试，修改代码，提交修改）	60	90
Reporting	报告
· Test Report	· 测试报告	30	60
· Size Measurement	· 计算工作量	15	5
· Postmortem & Process Improvement Plan	· 事后总结, 并提出过程改进计划	30	15
	合计	395	450
与预估时间相差较大的主要是在学习新技术方面，对c++的使用进行了学习，故使用了较长时间。

二.思路描述

基础题

看完题目之后第一时间想到的解法是暴力算出所有交点然后去除重复交点就可以得到最终答案。
要达到这个目标需要几个步骤：

• 根据给定两点\((x_0,y_0),(x_1,y_1)\)求出直线的一般式方程：

\[Ax+By+C=0 \]

通过计算我们可以得到：

\[A=y_1-y_0, B=x_0-x_1, C=x_1y_0-x_0y_1 \]

• 根据两直线一般式方程：

\[A_0x+B_0y+C_0=0,A_1x+B_1y+C_1=0 \]

令\(D=A_0B_1-A_1B_0\)
- 当\(D=0\)时，两直线平行
- 当\(D\ne0\)时，交点坐标为:

\[(\frac{B_0C_1-B_1C_0}{D}, \frac{A_1C_0-A_0C_1}{D}) \]

• 计算直线两两之间的交点并利用set类去重得到最后答案。

附加题：

• 计算直线与圆交点：
  将直线方程代入圆方程中计算一元二次方程的解即可(分斜率存在与不存在两种情况计算)。
• 计算圆与圆交点：
  将两圆方程相减，得到一直线的方程，然后求得该直线与其中一圆交点即为两圆交点。
• 最后将所有几何对象(直线和圆)之间的交点计算出之后去重即可。

三.设计实现

基础题

实现了一个Line类，Line类中属性有一般式方程\(Ax+By+C=0\)中的A,B,C三个参数，还有判断两直线是否平行的isParallel函数和计算两直线交点的findIntersection函数。
主要逻辑通过一个循环实现：读入直线的过程中对每一条直线生成Line类实例，如果该直线是第一条直线则直接将其加入容器，反之则计算该直线与容器中所有直线的交点并且加入set类实例。代码实现过程较为简单故没有画出流程图。

附加题

实现了一个circle类，类中有判断直线与圆是否有交点的函数isIntersectWithLine，求直线和圆交点的函数findIntersectWithLine，判断圆与圆是否有交点的函数isIntersectWithCircle和求圆和圆交点的函数findIntersectWithCircle。
逻辑与基础题类似，在读入几何对象的过程中将其与所有已读入的直线和圆求交点。

• 单元测试设计
  测试了直线的构造函数(包括边界情况和特殊情况)，判断两直线平行的函数(包括特殊情况)，计算两直线交点的函数(包括边界情况)
  结果如下
  

四.程序性能改进

时间大概为30分钟
一开始使用的方法是先将直线全部读入然后两两求交点，之后发现边读入边计算将会减少计算量。

• 性能分析:
  下面是对5000条直线，大概1000w个交点做的性能分析

  • 运行时间
    

  • 具体函数
    

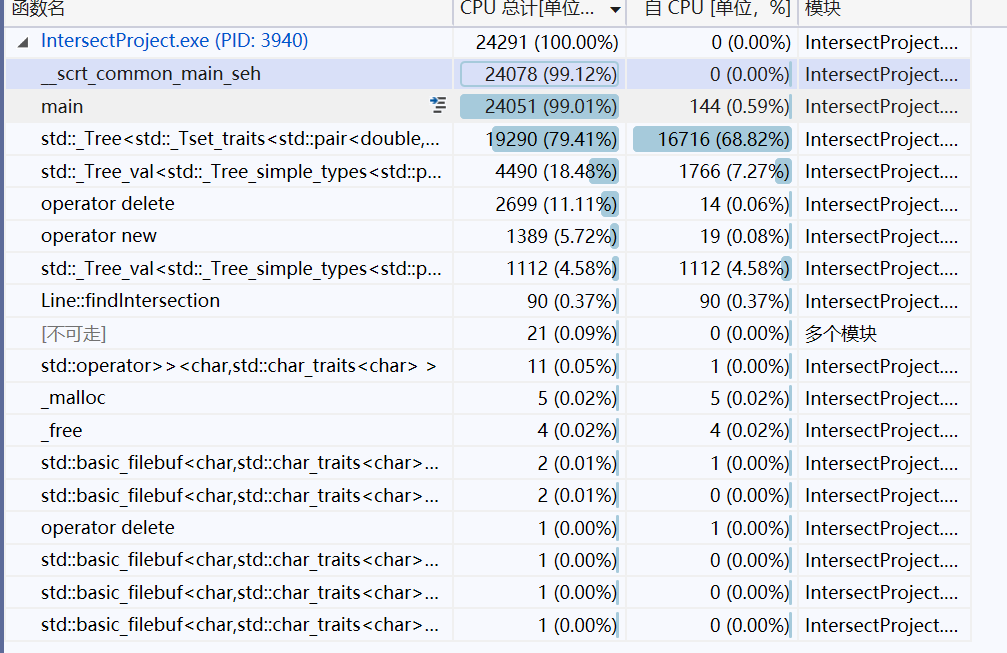
  • 进入具体代码发现是将交点加入points的语句即set排序过程开销最大
    

五.关键代码说明

基础题

如下代码中的A,B,C含义为直线一般式方程\(Ax+By+C=0\)中的对应参数

• Line类的构造函数，利用两点坐标及公式确定一般式方程

Line::Line(int x0, int y0, int x1, int y1)//利用直线上两点确定直线一般式方程
{
	A = (double)y1 - (double)y0;
	B = (double)x0 - (double)x1;
	C = (double)x1 * (double)y0 - (double)x0 * (double)y1;
}

• 判断平行的函数，直接利用公式判断即可

bool Line::isParallel(Line line) //判断是否平行
{
	double d;
	d = A * line.B - B * line.A;
	return d == 0;
}

• 利用公式计算两直线交点并返回

pair<double, double> Line::findIntersection(Line line) //找到两直线交点
{
	double d;
	d = A * line.B - B * line.A;
	double x;
	double y;
	x = (B * line.C - line.B * C) / d;
	y = (C * line.A - line.C * A) / d;
	return make_pair(x,y);
}

• 每读入一条直线就求其与容器中所有直线的交点

Line line(x0, y0, x1, y1);
if (!lines.empty()) {//判断是否为第一条直线
	for (size_t i = 0; i < lines.size(); i++) {
		if (!line.isParallel(lines.at(i))) {
                	points.insert(line.findIntersection(lines.at(i)));
		}
	}//计算该直线与容器中所有直线的交点并加入points
}
lines.push_back(line);

附加题

• 判断直线和圆是否相交

bool Circle::isIntersectWithLine(Line line) {
	double d;
	d = (line.A * x + line.B * y + line.C) / sqrt(line.A * line.A + line.B * line.B); //计算圆心到直线的距离
	return d <= r;
}

• 求直线和圆交点

void Circle::findIntersectWithLine(set<pair<double, double>>* points, Line line) {
	if (line.B != (double)0) {//斜率存在的情况
		double k = -line.A / line.B;//直线斜率
		double b1 = -line.C / line.B;//直线截距
		double s = b1 - y;//以下为将直线方程代入圆方程后的计算
		double a = k * k + 1;
		double b = 2 * x - 2 * k * s;
		double c = x * x + s * s - r * r;
		double tmp = sqrt(b * b - 4 * a * c);
		if (tmp == (double)0) {
			double x1 = b / (2 * a);
			double y1 = k * x1 + b1;
			points->insert(make_pair(x1, y1));
		}
		else {
			double x1 = (b + tmp) / (2 * a);
			double y1 = k * x1 + b1;
			points->insert(make_pair(x1, y1));
			double x2 = (b - tmp) / (2 * a);
			double y2 = k * x2 + b1;
			points->insert(make_pair(x2, y2));

		}
	}
	else {//斜率不存在的情况
		double p = - line.C / line.A;
		double q = sqrt(r * r - (p - x) * (p - x));
		if (q == (double)0) {
			points->insert(make_pair(p, y));
		}
		else {
			double y1 = y + q;
			points->insert(make_pair(p, y1));
			double y2 = y - q;
			points->insert(make_pair(p, y2));
		}
	}
}

• 判断圆和圆是否有交点

bool Circle::isIntersectWithCircle(Circle circle) {
	double x_d = x - circle.x;
	double y_d = y - circle.y;
	double d = sqrt(x_d * x_d + y_d * y_d);// 计算两圆心之间距离
	return (d <= (r + circle.r) && d >= fabs(r - circle.r));

}

• 计算圆和圆之间交点

void Circle::findIntersectWithCircle(set<pair<double, double>>* points, Circle circle) {
	double x1 = circle.x;
	double y1 = circle.y;
	double r1 = circle.r;
	double a = (2 * (x1 - x));
	double b = (2 * (y1 - y));
	double c = (x * x + y * y - r * r) - (x1 * x1 + y1 * y1 - r1 * r1);//计算两圆交点所在直线方程
	Line line(a, b, c);
	findIntersectWithLine(points, line);
}

六.代码风格检测

截图如下