《机器学习实战》读书笔记-1

 

#（本人开发工具为PyCharm，Python版本是3.5）

第二章 KNN

2.1 概述

k-紧邻算法的一般流程:

1. 收集数据：可以使用任何方法
2. 准备数据：距离计算所需要的数值，最好是结构化的数据格式
3. 分子数据：可以使用任何方法
4. 训练数据：此步骤不适应于k-紧邻算法
5. 测试数据：计算错误率
6. 使用算法：首先需要输入样本数据和结构化的输出结果，然后运行k-紧邻算法判定输入数据分别属于哪个分类，最后应用对计算出的分类执行后续的处理

2.1.1 准备数据

　　创建名为kNN.py的Python模块

import numpy as np
import operator

def createDataSet():
    group = np.array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
    labels = ['A','A','B','B']
    return group,labels

 

　　在文件夹中创建另外一个.py文件

import kNN

group,labels = kNN.createDataSet()
print('group = ',group,'\n','labels = ',labels)

　　运行结果：

group =  [[ 1.   1.1]
 [ 1.   1. ]
 [ 0.   0. ]
 [ 0.   0.1]] 
 labels =  ['A', 'A', 'B', 'B']

　　group中有四组数据，每组数据有两个属性或者特征值，labels包含了数据点的标签信息

2.1.2 实施kNN算法

　　对未知类别属性的数据集中的每个点依次执行以下操作：

1. 计算已知类别数据集中的点与当前点之间的距离
2. 按照距离递增次序排序
3. 选取与当前点距离最小的k个点
4. 确定前k个点所在类别的出现频率
5. 返回前k个点出现频率最高的类别作为当前点的预测分类　　　

程序清单2-1 k-紧邻算法

def classify0(inX,dataSet,labels,k):
    dataSetSize = dataSet.shape[0]   #取出dataSet的shape
    diffMat = np.tile(inX,(dataSetSize,1)) - dataSet    #将inX转换成与dataSet相同形状的数组
    sqDiffMat = diffMat**2
    sqDistances = sqDiffMat.sum(axis=1)
    distances = sqDistances**0.5
    sortedDistIndicies = distances.argsort()  #argsort()函数用法：从小到大排序，取其索引值index输出
    #print(sortedDistIndicies)
    classCount = {}
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
    #print(classCount)
    sortedClassCount = sorted(classCount.items(),key = operator.itemgetter(1),reverse=True)  #key=operator.itemgetter(1)意思是使用字典的第二个元素排序
    return sortedClassCount[0][0]

 

classify0（）函数的四个输入参数：inX是待分类的输入向量，dataSet是已知属性的样本集，labels是标签向量，k是选择最近邻居的数目。

import kNN

group,labels = kNN.createDataSet()
print('group = ',group,'\n','labels = ',labels)

print(kNN.classify0([0,0],group,labels,3))

输出结果：

group =  [[ 1.   1.1]
 [ 1.   1. ]
 [ 0.   0. ]
 [ 0.   0.1]] 
 labels =  ['A', 'A', 'B', 'B']
B

 

        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
    #print(classCount)
    sortedClassCount = sorted(classCount.items(),key = operator.itemgetter(1),reverse=True)  #key=operator.itemgetter(1)意思是使用字典的第二个元素排序
    return sortedClassCount[0][0]

 

2.2 示例：使用k-近邻算法改进约会网站的配对效果

1. 收集数据：提供文本文件
2. 准备数据：使用python解析文本文件
3. 分析数据：使用Matplotlib画二维扩散图
4. 训练算法：此步骤不适用于k-近邻算法
5. 测试算法：使用海伦提供的部分数据作为测试样本。测试样本和非测试样本的区别在于：测试样本是已经完成分类的数据，如果预测分类与实际类别不同，则标记为一个错误
6. 使用算法：产生简单的命令行程序，然后海伦可以输入一些特征数据以判断对方是否为自己喜欢的类型

2.2.1 准备数据从文本文件中解析数据

　　我们获得的文本是分类器不能识别的，所以我们要把它转换成分类器可以识别的类型。在kNN.py中创建名为file2matrix的函数，以此来处理文本数据格式的问题。该函数的输入为文件名字符串，输出为训练样本矩阵和类标签向量。

　　将下面代码增加到kNN.py中：

#从文本文件中解析数据
def file2matrix(filename):
    fr = open(filename)
    arrayOLines = fr.readlines()   #readlines()读取文件所有行，存储在一个list中，每行作为一个元素
    numberOfLines = len(arrayOLines)   #读取文件中元素数
    returnMat = np.zeros((numberOfLines,3))    #创建返回的Numpy矩阵
    classLabelVextor = []
    index = 0
    for line in arrayOLines:
        line = line.strip()  #移除字符串头尾指定的字符
        listFromLine = line.split('\t')  #使用tab字符 \t 将上一步得到的整行数据分割成一个元素列表
        returnMat[index,:] = listFromLine[0:3]  #前三列存储到特征矩阵中
        classLabelVextor.append(int(listFromLine[-1]))  #最后一列存储到标签矩阵中
        index += 1
    return returnMat,classLabelVextor

在另外一个kNN-1.py中：

datingDataMat,datingLabels = kNN.file2matrix('datingTestSet2.txt')
print(datingDataMat,'\n',datingLabels)

注意：使用函数file2matrix读取文件数据，必须确保数据集存储到工作目录下。

 

2.2.2 分析数据：使用matplotlib创建散点图

　　

import matplotlib
import matplotlib.pyplot as plt
import numpy as np

fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(datingDataMat[:,0],datingDataMat[:,1],15.0*np.array(datingLabels),15.0*np.array(datingLabels))
plt.show()

输出效果如下图：

 

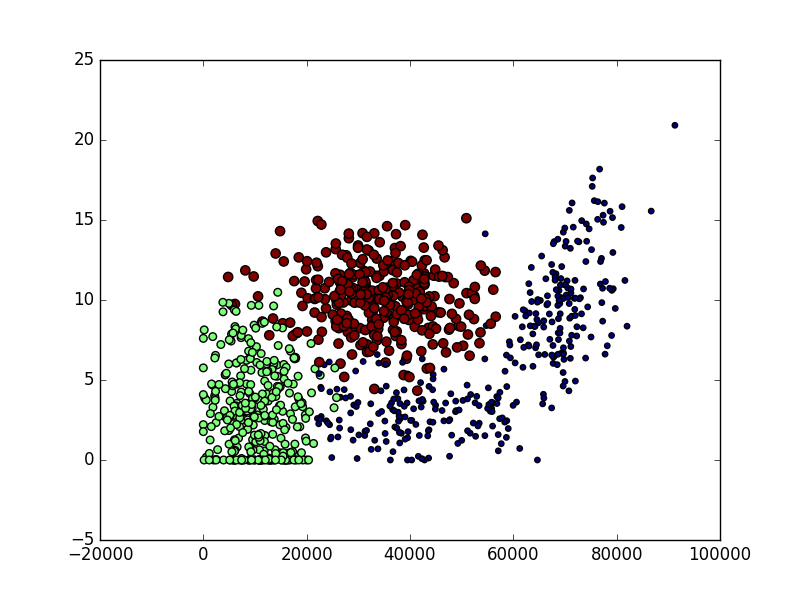
2.2.3 准备数据：归一化数值