用Java实现二叉查找树

二叉查找树的实现

1. 原理

　　二叉查找树，又称为二叉排序树、二叉搜索树。对于树中每一个节点X，它的左子树中所有项的值小于X中的项，而它的右子树中所有项的值大于X中的项。二叉查找树的平均深度为O(log N)，搜索元素的时间复杂度也是O(log N)。是两种库集合类TreeSet、TreeMap实现的基础。

2. public API

void makeEmpty( )      --> 置空
boolean isEmpty( )     --> 判空
AnyType findMin( )     --> 寻找最小值
AnyType findMax( )     --> 寻找最大值
boolean contains( x )  --> 是否存在元素x
void insert( x )       --> 插入元素x
void remove( x )       --> 删除元素x
void printTree( )      --> 遍历二叉树

3. 核心思想图解：递归

！寻找最小值

此处用递归实现：

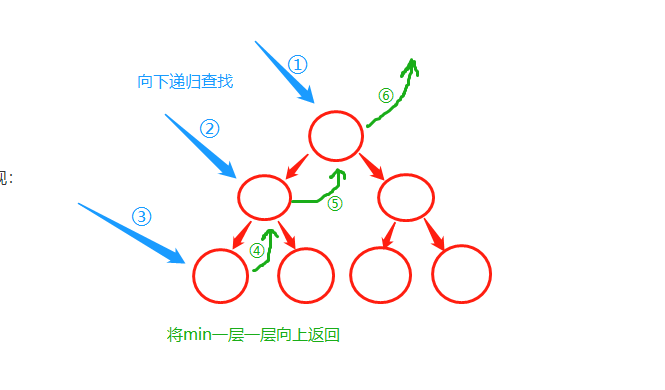
！寻找最大值

此处用非递归实现，也可以用递归实现：

！是否存在元素x

从root开始往下找，找到含有项X的节点，则此操作返回true，没有找到则返回false。

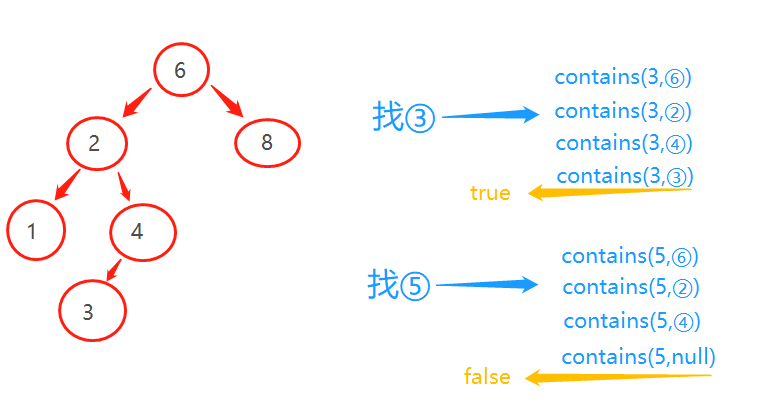
！插入元素x

从root开始往下找到合适的插入位置，然后插入。

！删除元素x

从root开始往下找到元素x，找到则删除，并且处理好后续工作。

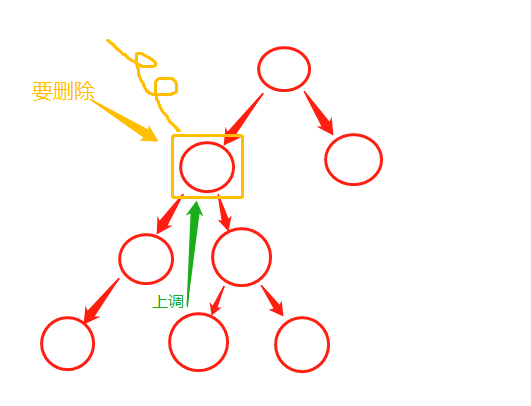
4. BinarySearchTree代码实现

类中，大量使用方法来调用递归方法的技巧，很好地体现了面向对象的封装性。

/**
 * @author: wenhx
 * @date: Created in 2019/10/8 19:41 （之前）
 * @description: 二叉查找树的实现
 */
public class BinarySearchTree<AnyType extends Comparable<? super AnyType>> {
​
    /**
     * 树的根节点
     */
    private BinaryNode<AnyType> root;
​
    /**
     * 定义树的节点（内部类）
     */
    private static class BinaryNode<AnyType> {
​
        AnyType element;            // 元素值
        BinaryNode<AnyType> left;   // 左孩子
        BinaryNode<AnyType> right;  // 右孩子
​
        // 节点的构造器：初始化一个树的节点
        BinaryNode(AnyType theElement) {
            this(theElement, null, null);
        }
​
        BinaryNode(AnyType theElement, BinaryNode<AnyType> lt, BinaryNode<AnyType> rt) {
            element = theElement;
            left = lt;
            right = rt;
        }
    }
​
    /**
     * 二叉排序树的构造器：初始化根节点
     */
    public BinarySearchTree() {
        root = null;
    }
​
    /**
     * 置空
     */
    public void makeEmpty() {
        root = null;
    }
​
    /**
     * 判空
     */
    public boolean isEmpty() {
        return root == null;
    }
​
    /**
     * 寻找最小值
     */
    public AnyType findMin() {
        if (isEmpty()) {
            throw new RuntimeException();
        }
        return findMin(root).element;
    }
​
    /**
     * 寻找最大值
     */
    public AnyType findMax() {
        if (isEmpty()) {
            throw new RuntimeException();
        }
        return findMax(root).element;
    }
​
​
    /**
     * 是否存在元素x
     */
    public boolean contains(AnyType x) {
        return contains(x, root);
    }
​
    /**
     * 插入元素x
     */
    public void insert(AnyType x) {
        root = insert(x, root);
    }
​
    /**
     * 删除元素x
     */
    public void remove(AnyType x) {
        root = remove(x, root);
    }
​
    /**
     * 遍历此二叉树
     */
    public void printTree() {
        if (isEmpty()) {
            System.out.println("Empty tree");
        } else {
            printTree(root);
        }
    }
​
    /**
     * 寻找最小值（内部方法）：此处用递归实现
     */
    private BinaryNode<AnyType> findMin(BinaryNode<AnyType> t) {
        if (t == null) {
            return null;
        } else if (t.left == null) {
            return t;
        }
        return findMin(t.left);
    }
​
    /**
     * 寻找最大值（内部方法）：此处用非递归实现
     */
    private BinaryNode<AnyType> findMax(BinaryNode<AnyType> t) {
        if (t != null) {
            while (t.right != null) {
                t = t.right;
            }
        }
        return t;
    }
​
    /**
     * 是否存在元素x（内部方法）
     */
    private boolean contains(AnyType x, BinaryNode<AnyType> t) {
        /**
         * 跳出递归的条件
         */
        if (t == null) {
            return false;
        }
​
        /**
         * 如果x小于节点值，则递归到左孩子；
         * 如果x大于节点值，则递归到右孩子；
         * 如果x等于节点值，则找到。
         */
        int compareResult = x.compareTo(t.element);
​
        if (compareResult < 0) {
            return contains(x, t.left);
        } else if (compareResult > 0) {
            return contains(x, t.right);
        } else {
            return true;
        }
​
    }
​
    /**
     * 插入元素x（内部方法）
     */
    private BinaryNode<AnyType> insert(AnyType x, BinaryNode<AnyType> t) {
        /**
         * 跳出递归的条件
         */
        if (t == null) {
            return new BinaryNode<>(x, null, null);
        }
​
        /**
         * 如果x小于节点值，则递归到左孩子；
         * 如果x大于节点值，则递归到右孩子；
         * 如果x等于节点值，则说明已有元素x，无需操作。
         */
        int compareResult = x.compareTo(t.element);
​
        if (compareResult < 0) {
            t.left = insert(x, t.left);
        } else if (compareResult > 0) {
            t.right = insert(x, t.right);
        } else {
        }
        return t;
​
    }
​
    /**
     * 删除元素x（内部方法）
     */
    private BinaryNode<AnyType> remove(AnyType x, BinaryNode<AnyType> t) {
        /**
         * 跳出递归的条件
         */
        if (t == null) {
            return t;   // Item not found; do nothing
        }
​
        /**
         * 如果x小于节点值，则递归到左孩子；
         * 如果x大于节点值，则递归到右孩子；
         * 如果x等于节点值，则要删除此节点。
         */
        int compareResult = x.compareTo(t.element);
​
        if (compareResult < 0) {
            t.left = remove(x, t.left);
        } else if (compareResult > 0) {
            t.right = remove(x, t.right);
        } else if (t.left != null && t.right != null) {
            // 要删除的节点有两个孩子（可选用右孩子最小元素/左孩子最大元素上调）
            t.element = findMin(t.right).element;
            t.right = remove(t.element, t.right);
        } else {
            // 要删除的节点有一个孩子或者没有孩子
            t = (t.left != null) ? t.left : t.right;
        }
        return t;
    }
​
    /**
     * 遍历此二叉树（内部方法）
     */
    private void printTree(BinaryNode<AnyType> t) {
        // 中序遍历-->即递增顺序
        if (t != null) {
            printTree(t.left);
            System.out.println(t.element);
            printTree(t.right);
        }
    }
​
    /**
     * 求树的深度（内部方法）
     */
    private int height(BinaryNode<AnyType> t) {
        if (t == null) {
            return -1;
        } else {
            return 1 + Math.max(height(t.left), height(t.right));
        }
    }
​
    /**
     * 主方法用来测试
     */
    public static void main(String[] args) {
        BinarySearchTree<Integer> t = new BinarySearchTree<>();
        t.insert(6);
        t.insert(3);
        t.insert(9);
        t.insert(2);
        t.insert(5);
        t.insert(8);
        t.insert(10);
        t.printTree();
        t.insert(4);
    }
}

 

okay，今天就到这啦，一定要掌握这种数据结构哈，真的很重要！！！