RSA加密

1.RSA加密原理：RSA中存在一对公钥（e,n）,和私钥（d,n）,密文等于明文的e次方除以n的余数（m=s^{e%n），明文等于密文的d次方除以n的余数（s=m}d%n）
下面展示公钥和密钥的制作过程：先选取两个质数p,q,n等于p乘上q（n=p*q）,求欧拉函数t=(p-1)(q-1),选取e(1<=e<=t)且要求e与t互质（gcd(e,t)=1）,则d为e在模n下的乘法逆元
2.RSA题型汇总：
1.共e攻击：特征有多组n和c，但只有一个e，且e的值很小，原理c1=m^e%n1,c2=me%n2……，本质上为中国剩余定理，题型简单在此不作赘述。
2.低加密指数攻击：特征e较小，原理：c=m^e%n,则me=c+kn,则遍历所有的k，找到能使c+kn刚好开e次方为整数即可，即直接爆破。题型简单不作赘述。
3.e与phin不互质的情况（1）：特征：gcd(e,phin)=t较小，原理：令e1=e/t,c=m^{e%n,即可变为c=(m}t)^e1%n,将mt看做一个整体，把e1看做公钥e，即可转变为正常的RSA题型来写，求出m^t,若开t次根号刚好为一个整数则直接求出，若不是则需要用其他的方法求出m。
4.共模攻击（1）：特征e1与e2互质，原理：c1=m^e1%n,c2=me2%n,由拓展欧几里得可知gcd(e1,e2)=e1s1+e2s2=1,用_,s,t=gcdext(e1,e2),m=c1^s1*c2s2%n即可。脚本简单自己写。
5.已知（e,dp,n,c）:dp=d%(p-1)

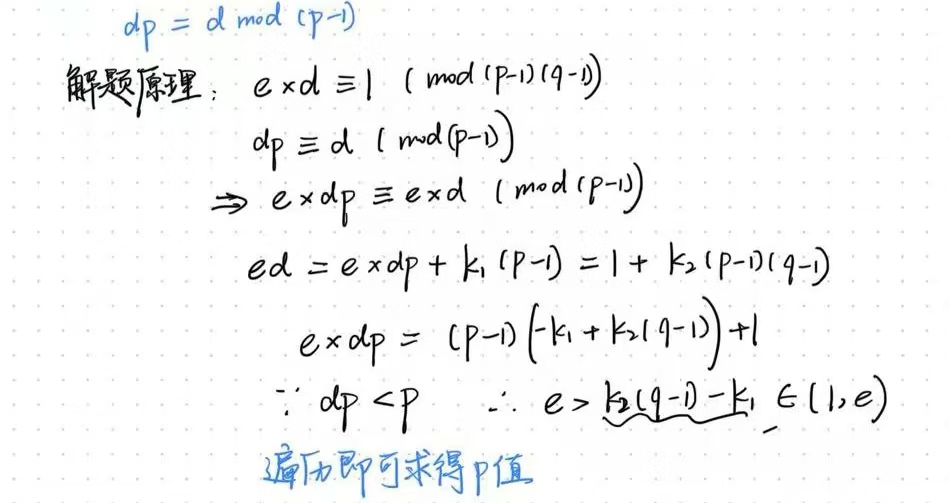
n =
e =
c =
dp =
import gmpy2
import binascii
for i in range(1, e):
if (e * dp - 1) % i == 0 and n % ((e * dp - 1) // i + 1) == 0:
q = n // ((e * dp - 1) // i + 1)
phi = (q - 1) * ((e * dp - 1) // i)
d = gmpy2.invert(e, phi)
m = gmpy2.powmod(c, d, n)
print(binascii.unhexlify(hex(m)[2:]))

 6.n为多个质数之积：特征：n=a*b*c*d*…，则此时欧拉函数phin=（a-1）(b-1)(c-1)(d-1)(…），其余方法相同，此题简单不作赘述。
 7.rabin:特征：e=2,p%4==3,q%4==3,此类题目需要用到中国剩余定理和二次剩余的知识

原理：
脚本：n =
p =
e = 2
c =
q=n//p
from gmpy2 import *
from Crypto.Util.number import *
import libnum
mp = pow(c, (p + 1) // 4, p)
mq = pow(c, (q + 1) // 4, q)
yp = gcdext(p, q)[1]
yq = gcdext(p, q)[2]
m1 = (yp * p * mq + yq * q * mp) % n
m2 = n - m1
m3 = (yp * p * mq - yq * q * mp) % n
m4 = n - m3
print(bin(m1), bin(m2), bin(m3), bin(m4))
m = int('0b111011001100101010100100111100101011111011010010110111001110100001100110111001001100101011100110011011101101001011011100110011101111101', 2)
print(m)
print(libnum.n2s(int(m)))

  8.维纳攻击：特征：d<(n^0.25)/3,q<p<2q,q和p非常大，且接近，n无法分解

n =
e =
c =
import gmpy2
import libnum
def continuedFra(x, y):
cf = []
while y:
cf.append(x // y)
x, y = y, x % y
return cf
def gradualFra(cf):
numerator = 0
denominator = 1
for x in cf[::-1]:
# 这里的渐进分数分子分母要分开
numerator, denominator = denominator, x * denominator + numerator
return numerator, denominator
def solve_pq(a, b, c):
par = gmpy2.isqrt(b * b - 4 * a * c)
return (-b + par) // (2 * a), (-b - par) // (2 * a)
def getGradualFra(cf):
gf = []
for i in range(1, len(cf) + 1):
gf.append(gradualFra(cf[:i]))
return gf
def wienerAttack(e, n):
cf = continuedFra(e, n)
gf = getGradualFra(cf)
for d, k in gf:
if k == 0: continue
if (e * d - 1) % k != 0:
continue
phi = (e * d - 1) // k
p, q = solve_pq(1, n - phi + 1, n)
if p * q == n:
return d
d=wienerAttack(e, n)
m=pow(c, d, n)
print(libnum.n2s(m))