写一个解二阶魔方的程序
本文需要读者有一定的魔方基础, 最起码也要达到十秒内还原二阶魔方的水平, 并且手上最好有一个二阶魔方, 否则文中的很多东西理解不了. 另外, 这里使用的算法是我自己写着玩的, 如果你需要更成熟和专业的算法, 可以看这个. 本文最终得到的程序效果如下:

一. 问题分析
1. 魔方的数据结构
要使用程序计算魔方的解法, 第一步就需要设计一种数据结构来储存当前的魔方状态. 二阶魔方有八个角块, 我们可以把它们依次用0-7编号:

左后方看不到的角就是7号角块. 然后, 每个角块还有角度信息, 我们把白色和黄色作为基本色, 角块的基本色朝上或者朝下, 角度记为0, 逆时针转动120度后角度为0的记为1, 顺时针转动120度后角度为0的记为2. 这样, 我们就可以通过两个数字来储存一个角块信息.
一个魔方有八个角块, 由于所有角块的位置都是相对的, 因此我们可以假设7号角块已经复原, 现在我们要用某个数据结构来表示剩余七个角块的状态. 为了提高运算速度并且方便查重, 我们可以使用一个二进制数字来表示当前的魔方状态.

上图这个长度为35的二进制数字, 可以分为七个部分, 从低位到高位这七个部分分别储存了上图中魔方七个角块位置上的实际角块信息. 每个角块信息都是一个长度为5的二进制数, 其中前三位表示角块的号码, 后两位表示角块的角度. 这样, 我们用一个数字就能表示魔方的状态.
基于以上, 一个已经复原的魔方, 它的状态就是下面的这串二进制数, 所有角块的角度都为0, 角块编号0-6从低到高排列:

2. 解法分析
本文算法的核心就是深度优先搜索, 通过遍历所有可能的移动找出可行的解法. 二阶魔方一共有URFLDB六个面可以转动, 但是考虑到转动的对称性, 以及角块位置的相对性, 在假设7号角块已复原的前提下, 我们实际上只需要转动URF这三个面.
二阶魔方的最远移动距离为11, 因此我们的递归深度到11就够了. 考虑到每个面都有三种转动角度(90度, 180度, 270度), 并且上一步操作的面不能和这一步相同, 因此在递归深度达到11的情况下, 可能的操作有3*3*(2*3)^10=544195584种, 而二阶魔方的状态数为7!*3^6=3674160种, 远小于操作数. 因此我们还需要在遍历过程中注意重复状态.
基于以上, 本文算法核心部分的伪代码如下:
解决函数: 参数:上一层操作的面,当前的递归深度,当前的魔方状态 返回值:布尔值 # 首先处理边界条件 如果当前的递归深度大于11: 返回 False 如果当前的魔方状态在之前出现过,且那时的递归深度比现在浅: 返回 False 如果当前的魔方状态是复原状态: 记录解法 返回 True 记录当前的状态 迭代URF三个面: 如果这个面不是上一层操作过的面: 迭代这个面的三种转动角度: 调用解决函数, 传入当前操作的面,当前的递归深度+1,转动后的魔方状态 如果解决了: 返回 True 返回 False
3. 还原7号角块
上面1, 2节的分析都是基于一个前提, 即7号角块已经复原了, 但是这个前提未必是成立的. 因此, 我们需要在运算之前加上一个步骤, 这个步骤不转动魔方的任何一面, 而是通过x,y,z方向的转体将7号角块还原到正确的位置上, 同时记录下这些xyz的操作. 在计算出魔方的解法之后, 再基于之前的xyz操作对解法进行修正.
4. 程序的结构和流程
基于以上分析, 我们程序的结构大致如下:

首先, 我们创建一个接口以方便外界的调用. 在获取到用户给出的数据之后, 首先通过解析层把用户给出的数据解析为上述的数据结构, 并且预处理还原7号角块, 然后将解析后的信息交给运算部分计算结果, 最后将结果基于之前的预处理进行修正, 将修正结果返回给用户.
二. 算法的核心部分
基于上一章的分析, 这个算法的核心部分应该接收一个以长度为35的二进制数字所表示的魔方状态, 然后通过URF的移动将这个状态转变为复原态, 并最终返回达到复原态所经历的移动路径.
1. cube结构体
魔方的求解过程会产生很多变量, 因此我们首先定义一个结构体来储存这些变量, 它们的作用会在后续体现:
type cube struct { prefix []string state uint64 moves [11]string moveLength uint8 seen map[uint64]uint8 solved bool ans string }
2. 转动魔方的面
魔方转动的本质就是改变旋转面上四个角块的位置和方向, 从而使魔方从某个状态移动到另一个状态. 由于我们把所有的角块信息都放在一个状态数字里面了, 因此在数据的层面, 转动这个魔方分为三个步骤: 首先, 将对应面的四个角块信息从状态数字中提取出来; 然后, 修改提取出来的四个角块的位置和方向信息; 最后, 将修改后的角块填回状态数字, 覆盖原有的信息. 这样我们就得到了转动后的状态.
基于以上的分析, 我们需要定义如下几个函数:
var layerDigits = map[string][4]int{ "U": [...]int{0, 1, 2, 3}, "R": [...]int{2, 5, 4, 3}, "F": [...]int{1, 6, 5, 2}, } // 这个函数从某个状态中获取指定层的角块信息 func extractCorners(state uint64, layer string) []uint8 { corners := make([]uint8, 4) for i, digit := range layerDigits[layer] { corners[i] = uint8((state & (0b11111 << (digit * 5))) >> (digit * 5)) } return corners } // 这个函数给定四个角块和它们所在的层,返回顺时针转动九十度后的四个角块 func turnCorners(corners []uint8, layer string) []uint8 { corners = append(corners[1:], corners[0]) if layer == "R" || layer == "F" { corners[1], corners[3] = turnCorner(corners[1], "f"), turnCorner(corners[3], "f") corners[0], corners[2] = turnCorner(corners[0], "r"), turnCorner(corners[2], "r") } return corners } // 这个函数将某个角块顺时针或逆时针转动120度,返回转动后的角块 // method为f则顺时针,为r则逆时针 func turnCorner(corner uint8, method string) uint8 { angle := corner & 0b11 if method == "f" { angle++ if angle == 3 { angle = 0 } } else if method == "r" { if angle == 0 { angle = 3 } angle-- } corner &= 0b11100 return corner | angle } // 这个函数把给定的角块信息填入某个状态的指定位置,返回修改后的状态 func fillCorners(state uint64, corners []uint8, layer string) uint64 { for i, digit := range layerDigits[layer] { state &= ^(0b11111 << (digit * 5)) state |= (uint64(corners[i]) << (digit * 5)) } return state }
这几个函数使用到了位运算, 如果对位运算还不够了解, 推荐看这篇文章.
通过上面几个函数, 我们就可以旋转魔方并得到旋转后的状态了. 首先, 通过extractCorners函数提取到指定的URF的某个面四个角块的信息数组, 每块的信息用一个长度为5的二进制数表示; 然后, 通过turnCorners函数将得到的数组中的元素位置进行交换, 这样就等同于交换了指定面四个角块的位置, 此外如果是R操作或者F操作, 角块的方向也会变化, 因此再创建一个turnCorner函数来单独修改单个角块的方向信息; 上述步骤完成后, 我们就得到了转动后的四个角块, 调用fillCorners将转动后的角块填入原state中, 得到的新state就是魔方转动后的状态.
3. 深度优先搜索
在实现了对魔方的转动后, 我们就可以开始搜索解法了. 遍历所有可能的操作, 直到经过这些操作后的魔方状态为还原态为止, 这样我们就得到了魔方的解法:
const restoredState = 0b11000101001000001100010000010000000 var layers = [...]string{"U", "R", "F"} var layerAngles = [...]int{1, 2, 3} func (c *cube) solve(lastLayer string, index uint8) bool { if index >= 11 { return false } else if moveLength, exists := c.seen[c.state]; exists && moveLength < index { return false } else if c.state == restoredState { c.moveLength = index c.solved = true return true } c.seen[c.state] = index state := c.state for _, layer := range layers { if layer == lastLayer { continue } corners := extractCorners(c.state, layer) for _, angle := range layerAngles { corners = turnCorners(corners, layer) c.state = fillCorners(state, corners, layer) c.moves[index] = fmt.Sprintf("%s%d", layer, angle) if c.solve(layer, index+1) { return true } } c.state = state } c.moves[index] = "" return false }
4. 代码测试
通过上面的一百行代码, 我们就完成了整个解魔方算法的核心部分. 对它简单地进行一点测试, 结果如下:
func test() { cb := &cube{ state: 0b01000000100110110100100101101000110, seen: make(map[uint64]uint8), } cb.solve("", 0) fmt.Println(cb.moves[:cb.moveLength]) }
输出结果如下:

经过多种情况的测试, 可以确定, 我们这个算法是可行的, 能够解出任意状态正确的二阶魔方.
三. 解析层
解析层需要做三件事: 首先, 解析用户给的魔方状态, 把数据转化为我们定义的结构类型; 然后, 完成7号角块复原的工作, 此时数据已经可以交给运算层去计算了; 最后, 把计算结果转化为用户需要的格式返回.
1. 用户层面的魔方数据结构
对于用户来说, 使用二进制数据来表示魔方状态显然是不方便也不直观的, 因此我们使用颜色来表示魔方的状态. 二阶魔方一共有2x2x6=24片, 我们用0-23给每片的位置进行编号:
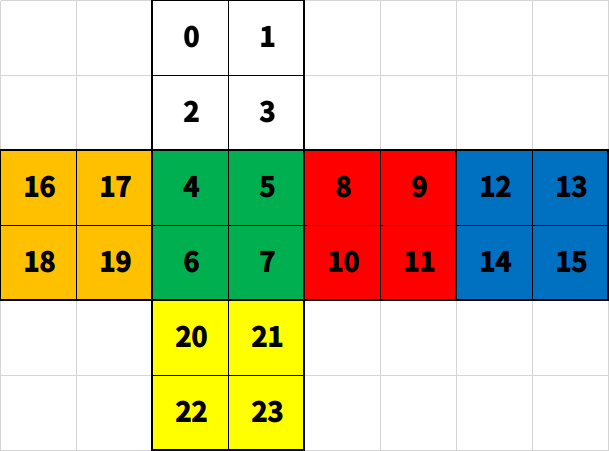
按照魔方复原之后白绿红蓝橙黄的顺序, 为这六个面的每个位置编号如上. 然后, 我们再使用WGRBOY六个字母代表六种颜色, 这样我们就能用一个长度为24的字符串来表示魔方的状态了, 字符串中第i位代表的就是上图中标号为i位置的颜色, 比如对于一个还原的魔方来说, 它的字符串为WWWWGGGGRRRRBBBBOOOOYYYY.
2. 用户数据的解析和验证
首先, 我们定义一个函数, 把用户给出的数据结构转变为二进制数字的数据结构:
var patternIndexes = [8][3]int{ {0, 16, 13}, {2, 4, 17}, {3, 8, 5}, {1, 12, 9}, {23, 11, 14}, {21, 7, 10}, {20, 19, 6}, {22, 15, 18}, } var cornerID = map[string]int{ "WOB": 0, "WGO": 1, "WRG": 2, "WBR": 3, "YRB": 4, "YGR": 5, "YOG": 6, "YBO": 7, } func patternToCorners(pattern string) []uint8 { if len(pattern) != 24 { panic(fmt.Sprintf("Invalid cube pattern")) } corners := make([]uint8, 8) for i := 0; i < 8; i++ { cornerPattern := make([]string, 3) var id, angle int for j, index := range patternIndexes[i] { cornerPattern[j] = string(pattern[index]) if cornerPattern[j] == "W" || cornerPattern[j] == "Y" { angle = j } } cornerPattern = append(cornerPattern[angle:], cornerPattern[:angle]...) if _, ok := cornerID[strings.Join(cornerPattern, "")]; ok { id = cornerID[strings.Join(cornerPattern, "")] } else { panic(fmt.Sprintf("Invalid corner:%v", cornerPattern)) } corners[i] = uint8((id << 2) | angle) } return corners }
每个角块都有编号和朝向两个属性, 我们首先从pattern中取出三片色块, 将它们组装为一个角块, 同时计算出这个角块的角度, 通过字典查找出角块的编号, 最后将角块编号和角块朝向结合起来就行了.
在解析完用户数据后, 我们还需要验证用户给的信息是否合法, 以避免无谓的计算. 一个二阶魔方状态合法的条件是: 0-7号角块都存在且唯一, 并且这些角块的朝向和为3的倍数. 因此, 我们使用如下的一个函数就能验证数据合法性:
func isCubeValid(corners []uint8) bool { existCorners := make([]bool, 8) var angleSum uint8 for _, corner := range corners { id, angle := corner>>2, corner&0b11 existCorners[id] = true angleSum += angle } for _, exist := range existCorners { if !exist { return false } } return angleSum%3 == 0 }
3. 还原7号角块
在第一章我们讲了, 可以通过x,y,z方向的整体移动来复原7号角块的位置和朝向. 因此, 我们首先就要定义三个函数, 这三个函数能够对刚解析得到的数据进行修改, 得到x,y,z移动之后的魔方状态:
func xMove(corners []uint8, times int) []uint8 { newCorners := make([]uint8, 8) for m, n := range []int{7, 0, 3, 4, 5, 2, 1, 6} { newCorners[m] = corners[n] } corners = newCorners for i, corner := range corners { if i%2 == 0 { corners[i] = turnCorner(corner, "r") } else { corners[i] = turnCorner(corner, "f") } } if times == 1 { return corners } return xMove(corners, times-1) } func yMove(corners []uint8, times int) []uint8 { corners = append(corners[1:4], corners[0], corners[7], corners[4], corners[5], corners[6]) if times == 1 { return corners } return yMove(corners, times-1) } func zMove(corners []uint8, times int) []uint8 { newCorners := make([]uint8, 8) for m, n := range []int{7, 6, 1, 0, 3, 2, 5, 4} { newCorners[m] = corners[n] } corners = newCorners for i, corner := range corners { if i%2 == 0 { corners[i] = turnCorner(corner, "f") } else { corners[i] = turnCorner(corner, "r") } } if times == 1 { return corners } return zMove(corners, times-1) }
这三个函数分别将魔方整体向x,y,z方向顺时针移动90度, 与上一章出现的turnCorners函数比较类似, 都是移动数组元素的位置, 有时候还需要修改角度. 只不过这里的数组长度变为8. 为了代码的简洁, 需要多次移动的情况使用递归调用来实现.
完成这三个函数之后, 我们就可以考虑如何复原7号角块了, 这里可以分为六种情况:
如果7号角块的角度为0:
如果7号角块在上层:
通过yMove移动到3号位置,然后通过两次zMove归位
如果7号角块在下层:
通过yMove归位
如果7号角块的角度为1:
如果7号角块在上层:
通过yMove移动到0号位置, 然后通过三次zMove归位
如果7号角块在下层:
通过yMove移动到4号位置, 然后通过一次zMove归位
如果7号角块的角度为2:
如果7号角块在上层:
通过yMove移动到0号位置, 然后通过三次xMove归位
如果7号角块在下层:
通过yMove移动到6号位置, 然后通过一次zMove归位
因为规律不明显, 所以这里只能硬编码了, 没有非常好的办法:
func getPrefix(corners []uint8) (newCorners []uint8, prefix []string) { var i int // 首先找出7号角块的位置 for j, c := range corners { if c>>2 == 0b111 { i = j break } } corner := corners[i] angle := corner & 0b11 if angle == 0 { if i > 3 { for j := 0; j < 7-i; j++ { corners = yMove(corners, 1) prefix = append(prefix, "Y") } newCorners = corners[:7] return } for j := 0; j < (i+1)%4; j++ { corners = yMove(corners, 1) prefix = append(prefix, "Y") } newCorners = zMove(corners, 2)[:7] prefix = append(prefix, []string{"Z", "Z"}...) return } else if angle == 1 { if i > 3 { for j := 0; j < (8-i)%4; j++ { corners = yMove(corners, 1) prefix = append(prefix, "Y") } newCorners = zMove(corners, 1)[:7] prefix = append(prefix, "Z") return } for j := 0; j < i; j++ { corners = yMove(corners, 1) prefix = append(prefix, "Y") } newCorners = zMove(corners, 3)[:7] prefix = append(prefix, []string{"Z", "Z", "Z"}...) return } else if angle == 2 { if i > 3 { yMoves := []int{2, 1, 0, 3} for j := 0; j < yMoves[i-4]; j++ { corners = yMove(corners, 1) prefix = append(prefix, "Y") } newCorners = xMove(corners, 1)[:7] prefix = append(prefix, "X") return } for j := 0; j < i; j++ { corners = yMove(corners, 1) prefix = append(prefix, "Y") } newCorners = xMove(corners, 3)[:7] prefix = append(prefix, []string{"X", "X", "X"}...) return } else { panic("It's impossible,haha") } }
在调用这个函数之后, 我们就复原了7号角块, 并且得到前置操作(x,y,z)和剩余0-6号角块组成的数组, 最后, 我们将这个数组转化为一个长度为35的二进制数字, 解析层的前期工作就算完成了:
var state uint64 for i, corner := range corners { state |= uint64(corner) << (i * 5) }
c.state = state
c.prefix = prefix
4. 格式化运算结果
在程序的运算层计算出结果之后, 我们还需要将运算结果与上一节得到的前置操作整合, 并最终格式化为用户需要的结果:
func mergeResult(prefix []string, moves []string) string { // 这个字典记录了x,y,z操作对层转动的影响, key为影响前,value为影响后 dic := map[string]map[string]string{ "X": { "U": "B", "R": "R", "F": "U", "L": "L", "B": "D", "D": "F", }, "Y": { "U": "U", "R": "B", "F": "R", "L": "F", "B": "L", "D": "D", }, "Z": { "U": "L", "R": "U", "F": "F", "L": "D", "B": "B", "D": "R", }, } for i := len(prefix) - 1; i >= 0; i-- { for j, move := range moves { moves[j] = dic[prefix[i]][move[:1]] + move[1:] } } return strings.ReplaceAll(strings.ReplaceAll(strings.Join(moves, " "), "3", "'"), "1", "") }
5. 步骤整合和异常处理
上述的步骤比较多和混乱, 并且有些步骤可能会抛出异常. 因此我们将这些步骤进行整合:
// New 函数解析和验证给定的图案,如果不合法,返回err,否则把解析结果创建cube对象返回 func New(pattern string) (c *cube, err error) { defer func() { if r := recover(); r != nil { var ok bool err, ok = r.(error) if !ok { err = fmt.Errorf("%v", r) } } }() state, prefix := parsePattern(pattern) c = &cube{ state: state, prefix: prefix, seen: make(map[uint64]uint8), } return } func parsePattern(pattern string) (state uint64, prefix []string) { corners := patternToCorners(pattern) if !isCubeValid(corners) { panic("Invalid cube pattern") } corners, prefix = getPrefix(corners) for i, corner := range corners { state |= uint64(corner) << (i * 5) } return }
这样我们就把解析层放在了实例化cube结构体之前的位置, 进行一些简单的测试, 结果如下:
func test() { c, _ := cube.New("WOWGGYGGRWWRBRBBBOOOYRYY") fmt.Println(c.Solve()) }

从一个包的角度来讲, 我们提供了一个简单易用的接口. 不过, 根本原因是目前提供的功能不多.
四. HTTP接口
为了让外界更方便地调用这个程序, 我们创建一个http服务器来提供接口:
import ( "encoding/json" "fmt" "log" "net/http" "time" "./cube" ) func cubeServer(w http.ResponseWriter, r *http.Request) { args, ok := r.URL.Query()["pattern"] if !ok || len(args) < 1 { return } res := map[string]interface{}{ "solved": true, "ans": "", "msg": "", } c, err := cube.New(args[0]) if err != nil { res["solved"] = false res["msg"] = err.Error() } else { start := time.Now().UnixNano() res["ans"] = c.Solve() fmt.Printf("用时%.3f秒\n", float64(time.Now().UnixNano()-start)/float64(1e9)) } bytes, _ := json.Marshal(res) w.Write(bytes) } func main() { http.HandleFunc("/", cubeServer) err := http.ListenAndServe("localhost:8080", nil) if err != nil { log.Fatal("ListenAndServe: ", err.Error()) } }
通过浏览器访问这个接口, 结果如下:

五. 客户端
为了让用户更加方便和直观地输入魔方状态, 我们可以创建一个客户端. 解决方案大致有前端, GUI和openCV三种, 这里使用python的tkinter模块完成一个GUI客户端:
from tkinter import * import json import requests URL = '127.0.0.1:8080' UNIT = 120 # 魔方一个块的大小,整个界面的布局基本由它决定 COLORS = ('white', 'green', 'red', 'blue', 'orange', 'yellow') FONT = ('charter', 14) class GUI: def __init__(self): self.root = Tk() self.root.title('魔方求解器') self.canvas = Canvas(self.root, width=UNIT * 8 + 10, height=6 * UNIT + 10) self.canvas.pack() # 各种组件往上加就完事了 self.url = self._add_url_text() self.info_bar = self._add_info_bar() self.current_color = COLORS[0] self.view = self._add_view() self.picks = self._add_color_picker() self._add_buttons() self.canvas.bind('<Button-1>', self._click) self.root.mainloop() def _add_url_text(self) -> Text: self.canvas.create_window(10, 10 + 0.5 * UNIT, anchor=NW, window=Label(text='服务器地址:', font=FONT)) txt_url = Text(height=1, width=20, font=FONT) txt_url.insert(INSERT, URL) self.canvas.create_window(10, 10 + 0.8 * UNIT, anchor=NW, window=txt_url) return txt_url def _add_info_bar(self) -> Text: self.canvas.create_window(10 + 4.1 * UNIT, 10 + 0.45 * UNIT, anchor=NW, window=Label(text='信息栏:', font=FONT)) info_bar = Text(height=4, width=40, font=FONT) self.canvas.create_window(10 + 4.1 * UNIT, 10 + 0.75 * UNIT, anchor=NW, window=info_bar) return info_bar def _add_view(self) -> [[[int]]]: # 创建展开图,返回展开图中所有块的id coordinate = ((1, 0), (1, 1), (2, 1), (3, 1), (0, 1), (1, 2)) view = [[[0] * 2 for _ in range(2)] for _ in range(6)] for f in range(6): for r in range(2): y = 10 + coordinate[f][1] * 2 * UNIT + r * UNIT for c in range(2): x = 10 + coordinate[f][0] * 2 * UNIT + c * UNIT view[f][r][c] = self.canvas.create_rectangle(x, y, x + UNIT * 0.95, y + UNIT * 0.95, fill=COLORS[f]) return view def _add_color_picker(self) -> [int]: # 创建调色板,返回调色板所有块的id picks = [0 for _ in range(6)] width = UNIT * 0.6 for i in range(6): x = (i % 3) * (width + 5) + UNIT * 4.5 y = (i // 3) * (width + 5) + UNIT * 4.5 picks[i] = self.canvas.create_rectangle(x, y, x + width, y + width, fill=COLORS[i]) self.canvas.itemconfig(picks[0], width=4) return picks def _add_buttons(self) -> None: self.canvas.create_window(10 + 6.6 * UNIT, 10 + 4.6 * UNIT, anchor=NW, window=Button(text='求解', height=1, width=10, relief=RAISED, command=self._solve, font=FONT)) self.canvas.create_window(10 + 6.6 * UNIT, 10 + 5.1 * UNIT, anchor=NW, window=Button(text='重置', height=1, width=10, relief=RAISED, command=self._reset, font=FONT)) def _solve(self) -> None: url = self.url.get(1.0, END) if not url.startswith('http'): url = f'http://{url}' try: r = requests.get(url, params={ 'pattern': ''.join( self.canvas.itemcget(char, 'fill')[0] for face in self.view for row in face for char in row).upper() }) assert r.status_code == 200 except: self._show_info('连接服务器失败,检查你的url和网络') return else: res = json.loads(r.text) if not res['solved']: self._show_info(f'求解过程中出现了问题: {res["msg"]}') else: self._show_info(f'这个魔方的解法是: {res["ans"]}') def _reset(self) -> None: for f, face in enumerate(self.view): for row in face: for i in row: self.canvas.itemconfig(i, fill=COLORS[f]) self._show_info('') def _click(self, _) -> None: # 响应canvas点击事件 click_id = self.canvas.find_withtag('current') if not click_id: return if click_id[0] in self.picks: # 如果点在颜色选择器上,就修改当前选中的颜色 self.current_color = self.canvas.itemcget('current', 'fill') for i in range(6): self.canvas.itemconfig(self.picks[i], width=1) self.canvas.itemconfig('current', width=5) else: # 否则就是点在展开图上,修改展开图对应块的颜色 self.canvas.itemconfig('current', fill=self.current_color) def _show_info(self, info: str) -> None: self.info_bar.delete(0.0, END) self.info_bar.insert(INSERT, info) if __name__ == '__main__': GUI()
这东西没有什么好讲的, 原理就是在画布上添加一些正方形, 然后通过点击事件给这些正方形上色. 最终成果如下:

六. 总结
经过一些测试之后, 发现部分状态的耗时时间明显比其它状态长很多:
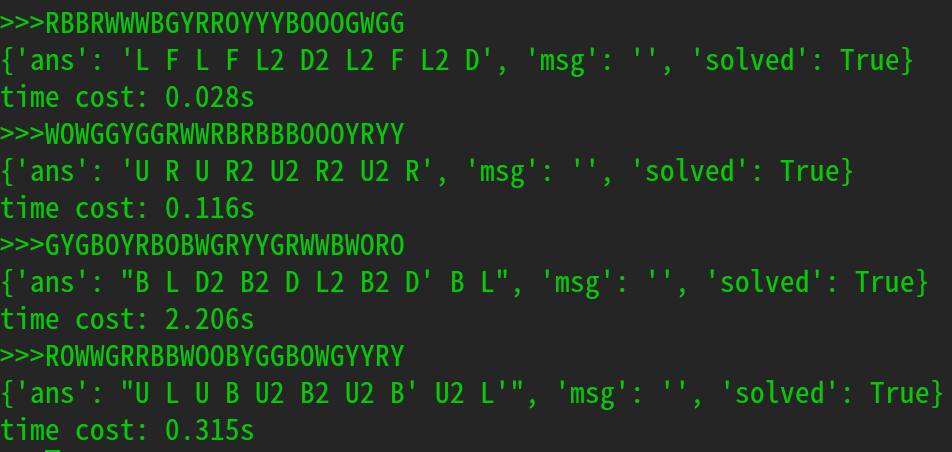
魔方的移动路径实际上是一颗树, 其高度只有11层, 而叶子节点的数量达到了3*3*(2*3)^10=544195584个, 因此, 这棵树是非常扁平的.

假设魔方的某个状态, 其还原步骤都在g的子树上, 我们使用深度优先搜索, 需要依次遍历b,c,d,e,f子树以及它们的所有子节点, 找不到之后才会去g寻找, 这样就会非常吃亏. 从这点来看, 使用广度优先搜索或许是更好的选择. 这部分就先挖个坑, 等哪天想起来了, 再研究研究.


