暴力破解SixPack问题

　　本文的内容是如何编写代码, 让计算机来解决SixPack拼图问题. 使用语言为Golang, 没有什么干货.

一. 问题分析

 　　最近从朋友那里拿到了一副拼图, 据说难度高达九级, 它大概长这样:

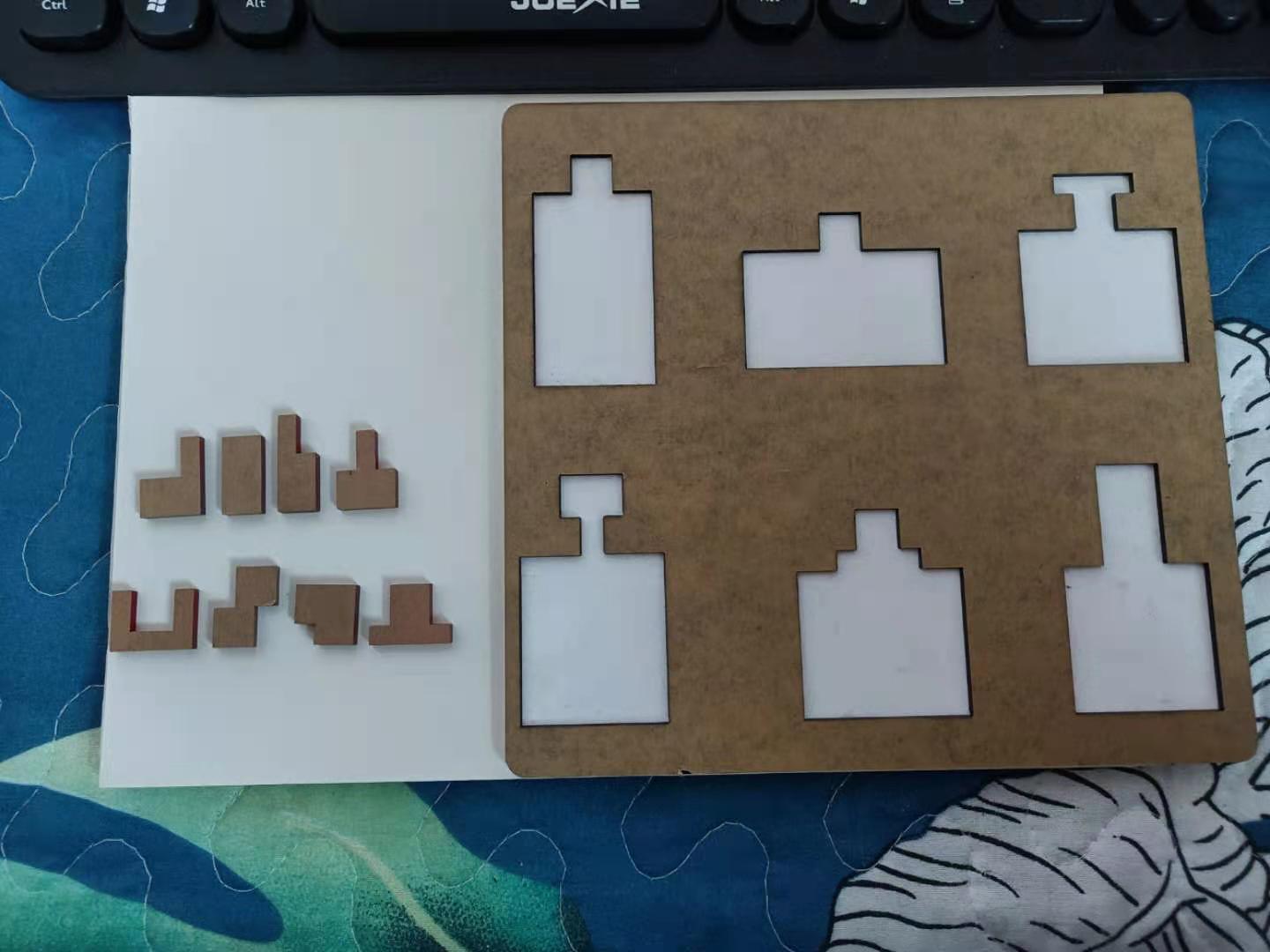
　　这幅拼图的目标是把八片拼图依次填满六个不同的空白位置. 八片拼图的每片都是由八个1x1大小的方块结合而成, 而给出的六个puzzle则是由64个1x1大小的空位组成. 因此, 这个问题用计算机的方式来描述就是: 如何将八个给定的二维数组结合成为指定形状.

　　由于状态数不多, 因此这里使用暴力破解的方式解决问题. 首先, 每片拼图都可以旋转和翻转, 因此我们需要计算出每片拼图的八个状态; 然后, 我们创建一个空白部分和puzzle一致的二维数组, 依次取出这八片拼图, 尝试每片拼图每种状态下所有可能放置的位置, 直到把所有拼图都放进去为止.

　　综上所述, 解决这个问题的伪代码如下:

解决函数:
    如果八片拼图都用完了:
        返回结果  # 边界条件
    从剩余拼图取出一片
    迭代这片拼图所有可能的状态:
        迭代拼图在这个状态下所有可能放入的位置:
            放入拼图
            继续调用自己
            如果得出结果, 就跳出循环
    放回拼图

二. Piece部分代码

 　　首先, 我们使用一个结构体来表示每片拼图:

type piece struct {
    basicShape     [][]string
    canRotateTwice bool
    canFlip        bool
    states         [][][]string
}

func (p *piece) GetStates() [][][]string {
    if len(p.states) < 1 {
        p.states = append(p.states, getDirections(p.basicShape, p.canRotateTwice)...)
        if p.canFlip {
            flippedShape := flipState(p.basicShape)
            p.states = append(p.states, getDirections(flippedShape, p.canRotateTwice)...)
        }
    }
    return p.states
}

// 调用这个函数获取某个状态不翻转情况下的所有朝向
// 如果拼图是中心对称的,得到两种朝向状态,否则得到四种
func getDirections(state [][]string, canRotateTwice bool) [][][]string {
    n := 2
    if canRotateTwice {
        n *= 2
    }
    result := make([][][]string, n)
    for i := 0; i < n; i++ {
        result[i] = state
        state = rotateState(state)
    }
    return result
}

// 返回拼图的某个状态顺时针转动九十度后的状态,不会修改原数据
func rotateState(state [][]string) [][]string {
    m, n := len(state[0]), len(state)
    result := make([][]string, m)
    for i := range result {
        result[i] = make([]string, n)
    }
    for i := 0; i < m; i++ {
        for j := 0; j < n; j++ {
            result[i][n-j-1] = state[j][i]
        }
    }
    return result
}

// 返回拼图的某个状态左右翻转后的状态,不会修改原数据
func flipState(state [][]string) [][]string {
    result := make([][]string, len(state))
    for i, list := range state {
        row := make([]string, len(list))
        for j := 0; j < len(list); j++ {
            row[j] = list[len(list)-j-1]
        }
        result[i] = row
    }
    return result
}

　　在实例化一片拼图时, 我们需要传入一个原始状态, 程序会通过旋转和翻转原始状态计算出这片拼图的所有八个状态, 然后调用GetStates方法就能获取这片拼图的所有状态. 由于有的拼图是左右对称或者中心对称的, 八个状态有重复, 因此我们还需要设置结构体的canRotateTwice和canFlip属性, 以减少不必要的重复状态.

　　最后, 这个piece结构体就可以通过下面的形式使用:

a := "A"
p := &piece{
    basicShape:     [][]string{{a, a, a, a}, {a, a, a, a}},
    canRotateTwice: false,
    canFlip:        false,
}
states := p.GetStates()

三. 递归部分代码

　　在计算出拼图的状态后, 下一个步骤就是把拼图填入到puzzle的空白部分中, 使用如下代码实现:

func tryToPut(state [][]string, puzzle [][]string, i int, j int) (bool, [][]string) {
    puzzle = copyPuzzle(puzzle)
    for a := 0; a < len(state[0]); a++ {
        for b := 0; b < len(state); b++ {
            if state[b][a] != empty {
                if puzzle[j+b][i+a] != empty {
                    return false, puzzle
                }
                puzzle[j+b][i+a] = state[b][a]
            }
        }
    }
    return true, puzzle
}

func copyPuzzle(puzzle [][]string) [][]string {
    result := make([][]string, len(puzzle))
    for i, list := range puzzle {
        row := make([]string, len(list))
        copy(row, list)
        result[i] = row
    }
    return result
}

　　由于拼图和puzzle都不是规则形状的, 因此我们在二维数组中设置一个empty变量来表示空白的部分. 一片拼图能够放入puzzle指定位置的条件是: 这片拼图的二维数组与puzzle二维数组相重叠的位置, 要么拼图是empty, 要么puzzle是empty.

　　能够放入拼图后, 剩下的就简单了. 根据第一节的伪代码写好一个递归函数就完事:

func solve(puzzle [][]string, i int) (bool, [][]string) {
    if i == len(piece.Pieces) {
        return true, puzzle
    }
    for _, state := range piece.Pieces[i].GetStates() {
        for _, nextPuzzle := range putIntoPuzzle(state, puzzle) {
            solved, result := solve(nextPuzzle, i+1)
            if solved {
                return solved, result
            }
        }
    }
    return false, [][]string{}
}

// 这个函数将一片拼图放入puzzle中,返回所有可以放置的结果,不会对原puzzle切片产生影响
func putIntoPuzzle(state [][]string, puzzle [][]string) [][][]string {
    result := [][][]string{}
    for i := 0; i < len(puzzle[0])-len(state[0])+1; i++ {
        for j := 0; j < len(puzzle)-len(state)+1; j++ {
            ok, newPuzzle := tryToPut(state, puzzle, i, j)
            if ok {
                result = append(result, newPuzzle)
            }
        }
    }
    return result
}

　　最后, 我们运行solve函数, 并且把结果写入文本文件中:

func main() {
    var startTime int64
    outputFile, outputError := os.OpenFile("res.txt", os.O_WRONLY|os.O_CREATE, 0666)
    if outputError != nil {
        panic("无法打开res.txt文件!!!")
    }
    defer outputFile.Close()
    outputWriter := bufio.NewWriter(outputFile)
    for i, puzzle := range puzzles {
        startTime = time.Now().UnixNano()
        solved, result := solve(puzzle, 0)
        if solved {
            fmt.Fprintf(outputWriter, "puzzle%d和对应解法,用时%.2f秒\n\n", i+1, float64(time.Now().UnixNano()-startTime)/float64(1e9))
            writePuzzle(outputWriter, merge(puzzle, result), true)
        } else {
            fmt.Fprintf(outputWriter, "没能解开puzzle%d,用时%.2f秒\n\n", i+1, float64(time.Now().UnixNano()-startTime)/float64(1e9))
            writePuzzle(outputWriter, puzzle, false)
        }
        outputWriter.Flush()
    }
}

四. 总结

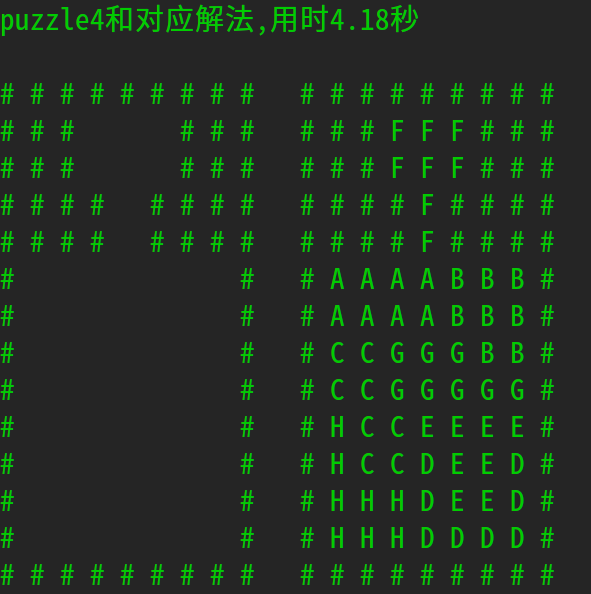
　　运行程序, 问题完美解决. 结果如下: