树状数组
落笔记下自己的感悟,本文章主要针对与lowbit函数的讲解,单点修改、单点询问与区间询问(用树状数组解决);
当遇到区间修改时,树状数组也能搞定,但是毕竟复杂,没有线段树更实在(线段树的延迟更新)。
lowbit函数
定义:在二进制状态下,最后一位1与其后面的零所构成的数值。
例如: (12)10进制 ------进制转换------ (1100)2进制
上例,红色部分(100)即是末尾1与其后面的零构成的数值。其值转成十进制为4;
所以 lowbit(12) = 4;
如何用代码实现lowbit函数?
不难发现,实现方法: lowbit(n)=n&(~n+1)
然后又发现 (~n+1) 不就是取反加1嘛,不就是-n的补码?
然后计算机存储的是补码,所以总结: lowbit(n)= (n)&(-n)
树状数组的实现原理
给出下图,已经建立好了树状数组。
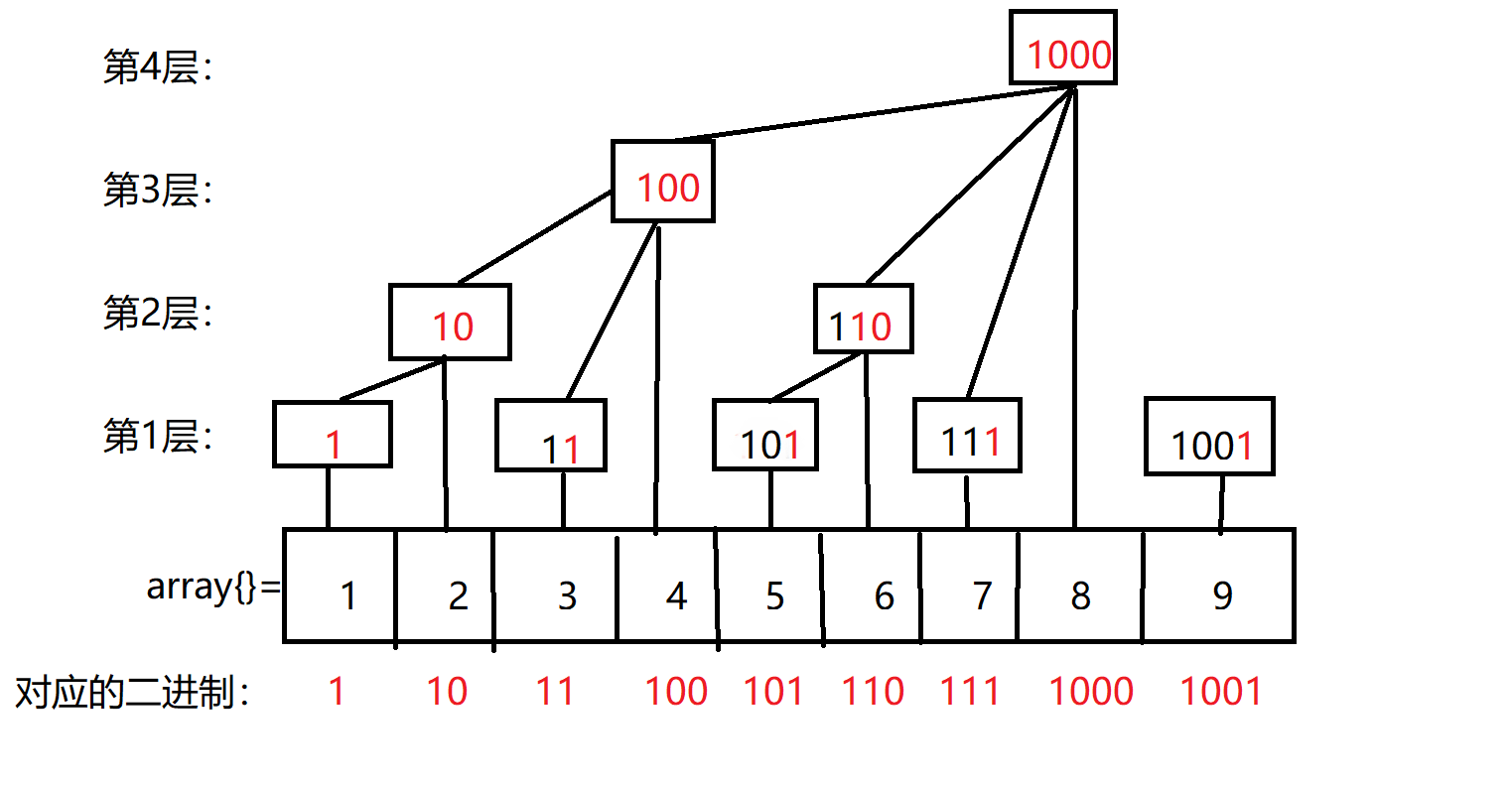
树上结点数值的红色部分即lowbit函数值,也是该结点存下的区间长度值。
例1:
树结点4, lowbit(4)=(100)2 = 4, 区间长度为4,即存下4个数(分别是数组结点1,2,3,4)
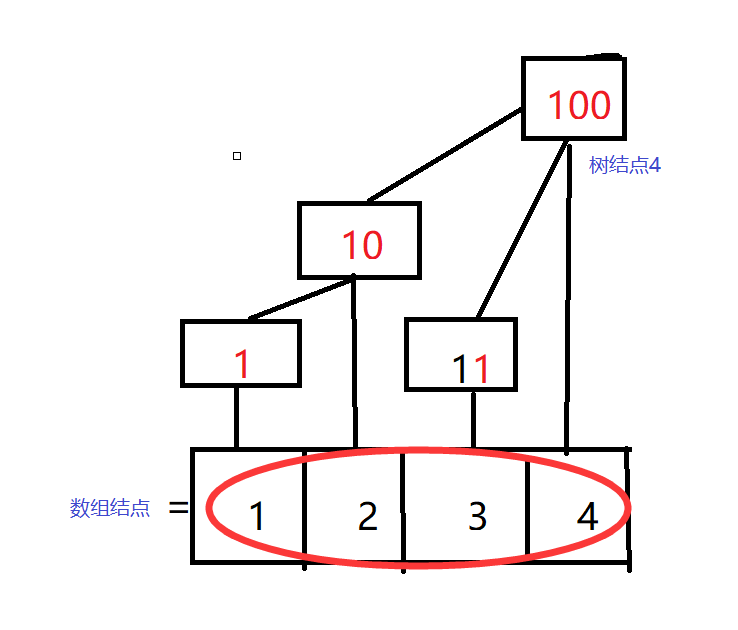
例2:
树结点6,lowbit(6)=(10)2 = 2,存长度为2的数值,分别是array【5】、array【6】

规律
1.建立的树状数组上,每一层的lowbit函数值相等。
2.lowbit函数值记录的是 区间长度。
3.树上编号为x的节点, 他的父节点编号为x+lowbit(x)
4.整棵树的深度为: (log2n )+ 1
5.找下一个结点 x-=lowbit(x)
代码
当要单点更新时,先更新底层,然后依次更新其父节点,一直到根结点。
用代码实现则运用上述规律3。
1 int lowbit(int n){ 2 return n&(-n); 3 } 4 5 6 //在叶节点x 增加 数值k 7 void add(int x,int k){ 8 for (;x<=n;x+=lowbit(x)){ 9 root[x]+=k; 10 } 11 }
区间查询运用规律5
1 int lowbit(int n){ 2 return n&(-n); 3 } 4 5 // 区间查询 6 7 int ask(int x){ 8 int ans=0; 9 for (;x;x-=lowbit(x)) 10 ans+=root[x]; 11 return ans; 12 }
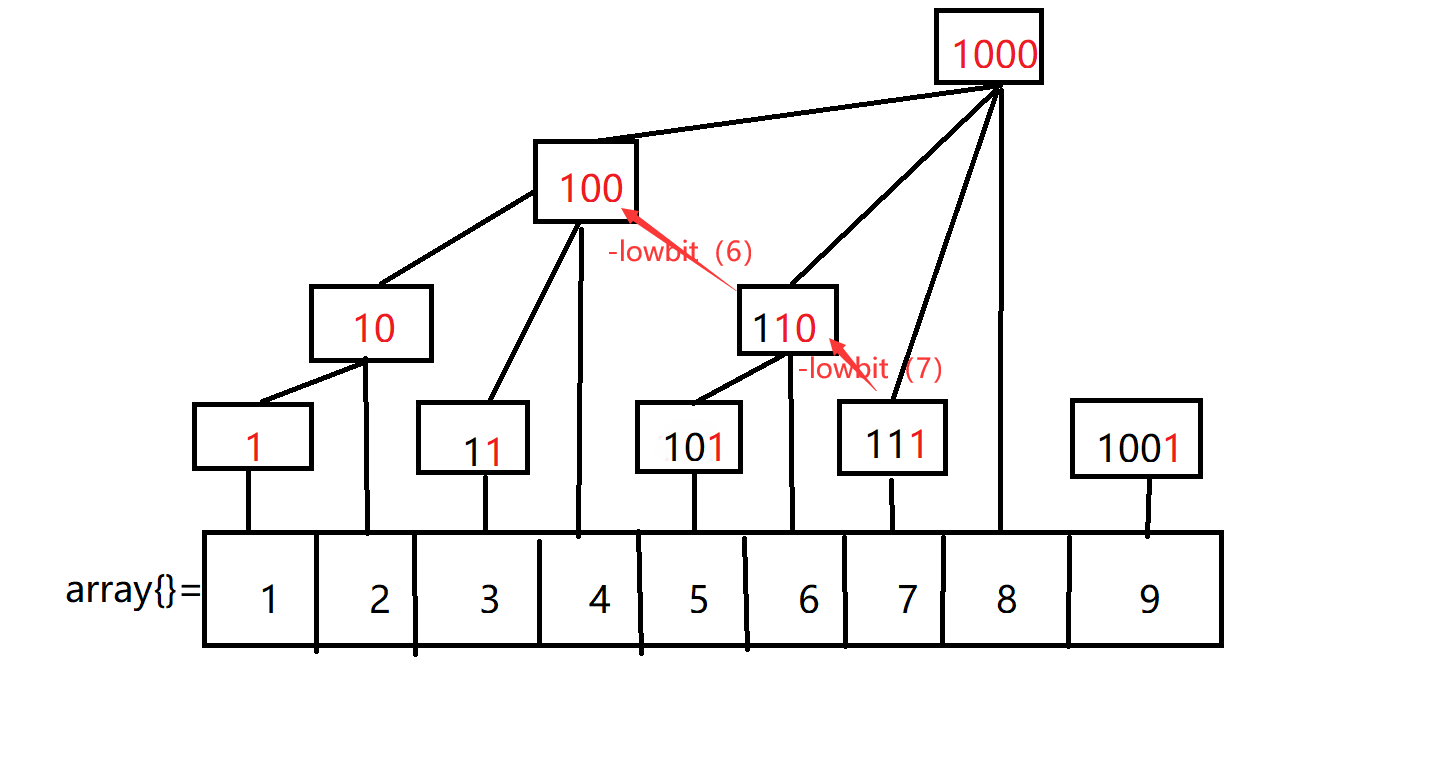
例如上图查询区间【1,7】的和 == root【7】+root【6】+root【4】
当遇到查询【l,r】区间和时,我们应该知道树状数组大多是用来维护前缀和的,那么只要查询两次区间和 ,然后【1,r】减去【1,l-1】就是答案。



