数论——终结素数判定

 

1.基础版（暴力）素数判定：

bool prime(int n) 
{
    if (n<=1)
        return false;
    int tmp=sqrt(n);
    for (int i=2;i<=tmp;i++)
        if (n%i==0)
            return false;
    return true;
}

 

2.再诉说一个素数规律。

 

//任何一个数都可以写成  6n,6n+1,6n+2,6n+3,6n+4,6n+5这种格式。

//显然6n , 6n+2 , 6n+4   能被2整除  
//      6n+3               能被3整除     
//因此满足上述格式的都为合数。

//只有满足  6n+1或6n+5 才有可能是素数。
//同时6n+5可以看成6n-1的另一种形式。
//即素数满足   6n-1和6n+1的形式 （除特例：2和3） 
//即结论：一个数若是素数，则他一定在6倍数的两边（除特例：2和3） 

 

　　故可以将上述代码再进行优化剪枝。

bool prime(int n)  
{
    if (n<=1)   //1即不是素数，又不是合数 
        return false;
    else if (n==2||n==3)
        return true;
    else if (n%6!=1&&n%6!=5)
        return false;
    int tmp=sqrt(n);
    for (int i=5;i<=tmp;i+=6)
        if (n%i==0||n%(i+2))
            return false;
    return true;
}

 

3.有的时候，面临的问题是询问次数过多，这里就需要通过一定的预处理，将询问的复杂度降为O(1)。

　　显然这里的预处理就是    线性素数筛。

 

 

原理：n为素数，那么 i * n （i为非1的任意自然数）是非素数，即将 i * n 筛去。

 

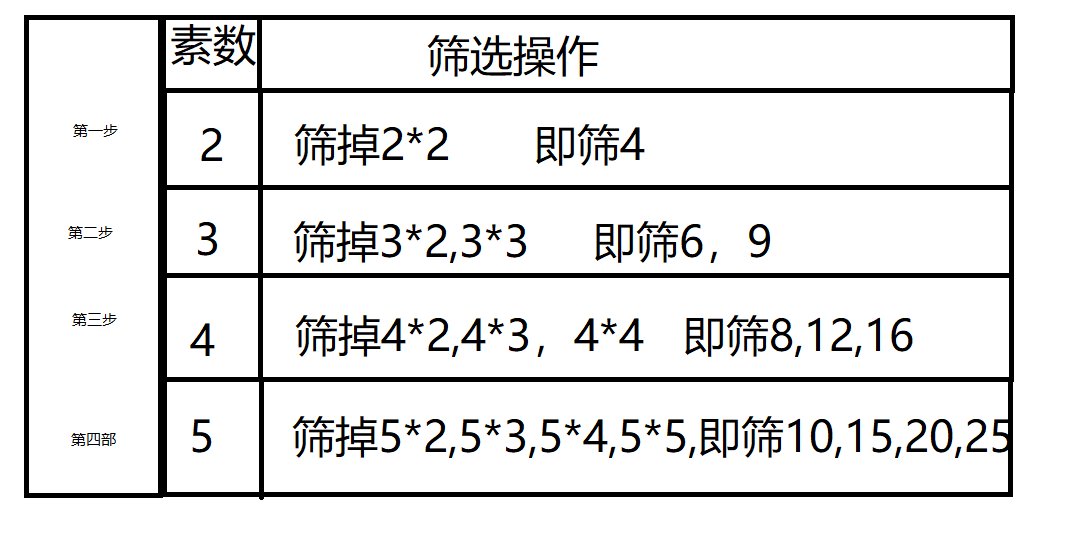
原理很简单，但是我们面临的优化是如何将一个数尽可能的只筛一次。  看下图操作

 

 

如下图模拟线性素数筛步骤    ：

 

 

 

代码：

 

const int MAX=10000010;   //线性素数筛的数据极限为1e7，大于这极限，则需要另寻他路 
bool is_prime[MAX+10];
int prime[MAX+10];
int cnt=0;
void init()
{
    is_prime[1]=true;
    
    for (int i=2;i<=10000010;i++){
        if (is_prime[i]==false)  
            prime[++cnt]=i;
        for (int k=1;k<=cnt&&i*prime[k]<=10000010;k++){
            is_prime[i*prime[k]]=true;
            if (i%prime[k]==0)
                break;
        }
    }
}

 

 

4.当我面临的数据超过了线性素数筛极限（1e7）的时候，那我如何处理？

 

　　答案：再引进一个算法　　Miller-Rabbin素数   ，    这是一个logn级别的算法  ， 这是一个开挂的算法。

 

 

//　　　　　　在学习该算法之前，应当了解    费马小定理。  

//　费马小定理：简单言之：   

//　假设p的素数，   那么 pow(a,p-1)≡1(%p) ,即pow（a,p-1）%p = 1


//那么如果有此式成立，是否p一定为质数？答案是否定的。但是，我们可以多测试几次，
//即随机选取a值进行测试，提高准确率。测试次数越大，正确率越高。(有一点随机数味道，一般a的取值次数在30次左右就能判定)

//优点：  算法数据极限可扩展到   int64 ，有点强。

//缺点：  测试一次失败的概率为  1/4，   测试30次失败的概率为    （1/4)^30。   即并非正确率100%