组合数+费马大/小定理

 

 

 

 

 

 

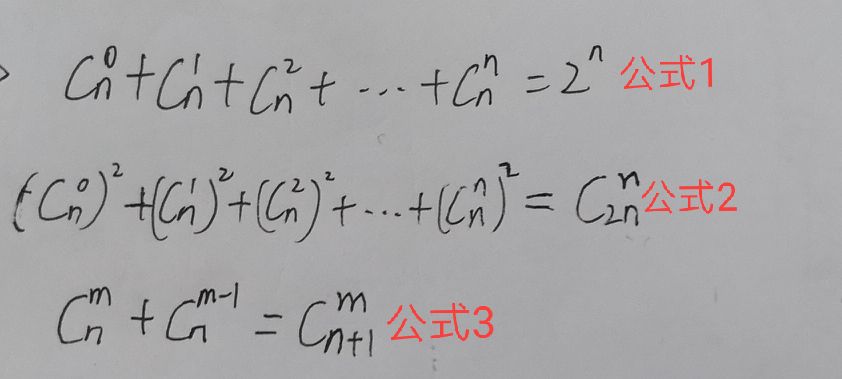
附上一题：  https://ac.nowcoder.com/acm/contest/114/B

 

 

有上面的公式2，还不能完全解决问题，这里还要用到阶乘的逆元。

 

我们都知道对于取模。

 a*b%mod   等价于    ((a%mod)*(b%mod))%mod

 

但是  (a/b)%mod   与    ((a%mod)/(b%mod))%mod 是非等价关系的。

 

题目要求取出  C(2*n,n);  的值，  也就是  2*n的阶乘连除以两个n的阶乘，而除法取模不满足结合律，所以此处要用到逆元。

 

先举一个简单的例子     a/b%mod   可以看成   a  *  pow(b,-1)%mod    那么此处是可以用取模结合律的，pow(b,-1)正是b关于1的逆元。

 

那么怎么求阶乘的逆元呢？也就是n的阶乘关于mod的逆元呢？ 

 

如果按照上面直接求关于1 的逆元，那么在计算机存储中，肯定是会超过double的精度的。因此这种解法是被否决的。

 

费马小定理：    假设a为整数，b为质数，且gcd(a,b)的值为1，也就是a,b互质，　　 　　那么可得     a^(b-1)%b==1

 

既然关于1 的逆元会被否决，那么求关于mod的逆元呢？      （证明过程）

 

a    *   （a关于mod的逆元）%mod的值应等于1 。     根据费马小定理，     a^(mod-1)%mod的值为1           那么a^(mod-1)     是否可以写成  a  *  a^(mod-2)?

 

综上所述，结论为：

　　　　　　a关于mod的逆元为    a^(mod-2)%mod ==1

 

 

AC代码：

#include<iostream>
#define N 2000010
#define ll long long
using namespace std;
int mod=998244353;
ll a[N],b[N];// 阶乘    和   逆元 
ll quick(ll a,ll b)
{
    ll ans=1;
    while (b){
        if (b&1)
            ans=ans*a%mod;
        a=a*a%mod;
        b>>=1;
    }
    return ans;
} 
void init()
{
    a[1]=a[0]=1;
    for (ll i=2;i<N;i++){
        a[i]=a[i-1]*i%mod;
    }
    b[N-1]=quick(a[N-1],mod-2);
    for (ll i=N-2;i>=0;i--){
        b[i]=b[i+1]*(i+1)%mod;
    }
    return ;
}
int main()
{
    ios::sync_with_stdio(false);
    int n;
    init();
    while (cin>>n){
        ll ans=0;
        for (int i=1;i<=n;i++){
            ans=(ans+(a[2*i]*b[i]%mod)*b[i])%mod;
        }
        cout<<ans<<endl;
    }
    return 0;
}

 

 

另外补充一下，费马大定理。

问题：a为整数，是否可以把该指数   a^p  （其中p>2）   拆分成两个整数p次幂的和呢？

费马大定理告诉你，这是不可能的。   （证明过程过于复杂，直接贴结论）

x^n+y^n= z^n       （其中x，y，z都是整数）        （费马大定理：当n大于2的时，则该方程不存在整数解。）