vector的二维用法+前缀和

题目链接：https://codeforces.com/contest/1082/problem/C（C. Multi-Subject Competition）

 

A multi-subject competition is coming! The competition has mm different subjects participants can choose from. That's why Alex (the coach) should form a competition delegation among his students.

He has nn candidates. For the ii-th person he knows subject sisi the candidate specializes in and riri — a skill level in his specialization (this level can be negative!).

The rules of the competition require each delegation to choose some subset of subjects they will participate in. The only restriction is that the number of students from the team participating in each of the chosen subjects should be the same.

Alex decided that each candidate would participate only in the subject he specializes in. Now Alex wonders whom he has to choose to maximize the total sum of skill levels of all delegates, or just skip the competition this year if every valid non-empty delegation has negative sum.

(Of course, Alex doesn't have any spare money so each delegate he chooses must participate in the competition).

Input
The first line contains two integers nn and mm (1≤n≤1051≤n≤105, 1≤m≤1051≤m≤105) — the number of candidates and the number of subjects.

The next nn lines contains two integers per line: sisi and riri (1≤si≤m1≤si≤m, −104≤ri≤104−104≤ri≤104) — the subject of specialization and the skill level of the ii-th candidate.

Output
Print the single integer — the maximum total sum of skills of delegates who form a valid delegation (according to rules above) or 00 if every valid non-empty delegation has negative sum.

Examples
input
6 3
2 6
3 6
2 5
3 5
1 9
3 1
output
22
input
5 3
2 6
3 6
2 5
3 5
1 11
output
23
input
5 2
1 -1
1 -5
2 -1
2 -1
1 -10
output
0
Note
In the first example it's optimal to choose candidates 11, 22, 33, 44, so two of them specialize in the 22-nd subject and other two in the 33-rd. The total sum is 6+6+5+5=226+6+5+5=22.

In the second example it's optimal to choose candidates 11, 22 and 55. One person in each subject and the total sum is 6+6+11=236+6+11=23.

In the third example it's impossible to obtain a non-negative sum.

A multi-subject competition is coming! The competition has mm different subjects participants can choose from. That's why Alex (the coach) should form a competition delegation among his students.

He has nn candidates. For the ii-th person he knows subject sisi the candidate specializes in and riri — a skill level in his specialization (this level can be negative!).

The rules of the competition require each delegation to choose some subset of subjects they will participate in. The only restriction is that the number of students from the team participating in each of the chosen subjects should be the same.

Alex decided that each candidate would participate only in the subject he specializes in. Now Alex wonders whom he has to choose to maximize the total sum of skill levels of all delegates, or just skip the competition this year if every valid non-empty delegation has negative sum.

(Of course, Alex doesn't have any spare money so each delegate he chooses must participate in the competition).

Input

The first line contains two integers nn and mm (1≤n≤1051≤n≤105, 1≤m≤1051≤m≤105) — the number of candidates and the number of subjects.

The next nn lines contains two integers per line: sisi and riri (1≤si≤m1≤si≤m, −104≤ri≤104−104≤ri≤104) — the subject of specialization and the skill level of the ii-th candidate.

Output

Print the single integer — the maximum total sum of skills of delegates who form a valid delegation (according to rules above) or 00 if every valid non-empty delegation has negative sum.

Examples

input

Copy

6 3
2 6
3 6
2 5
3 5
1 9
3 1

output

Copy

22

input

Copy

5 3
2 6
3 6
2 5
3 5
1 11

output

Copy

23

input

Copy

5 2
1 -1
1 -5
2 -1
2 -1
1 -10

output

Copy

0

Note

In the first example it's optimal to choose candidates 11, 22, 33, 44, so two of them specialize in the 22-nd subject and other two in the 33-rd. The total sum is 6+6+5+5=226+6+5+5=22.

In the second example it's optimal to choose candidates 11, 22 and 55. One person in each subject and the total sum is 6+6+11=236+6+11=23.

In the third example it's impossible to obtain a non-negative sum.

题目意思：

　　给定n（备选人数）,m（科目数目）。

　　后n行输入,每行两个整数，x和y

　　第i行输入，第i个学生     第x科目的y等级

　　输出等级之和最好情况（唯一要求是      参赛的科目中人数是相等的）

 

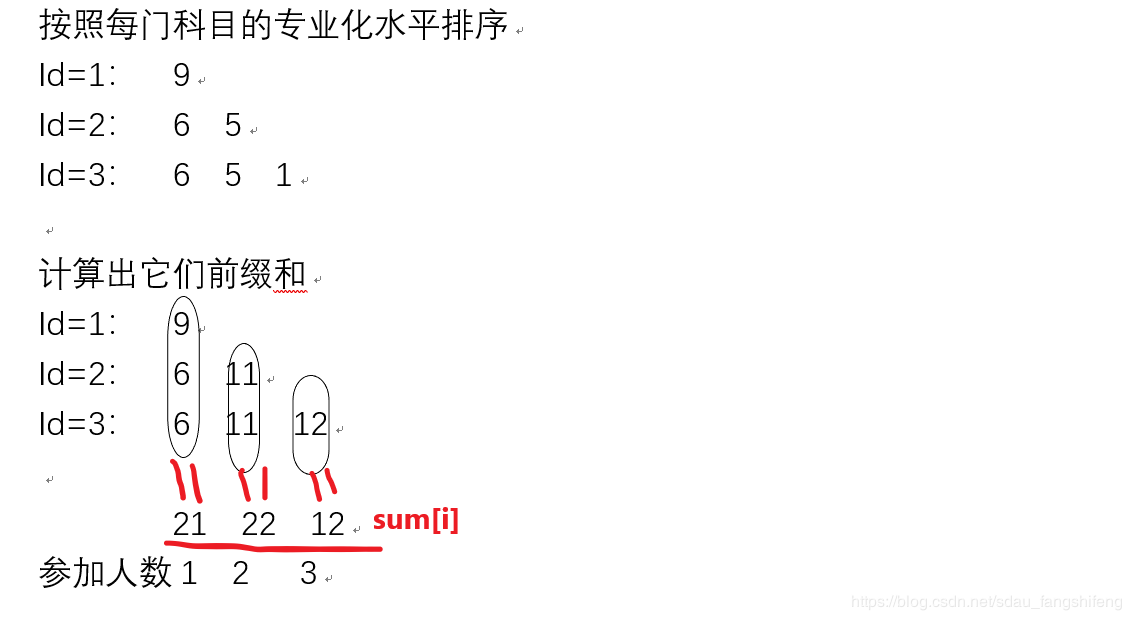
 盲点：

　　对于vector 类型来说，存在下列参数  greater<int>()  和less<int>(）

 

1. sort(v[i].begin(),v[i].end(),greater<int>());　　//默认从大到小
2. sort(v[i].begin(),v[i].end(),less<int>());　　　　//默认从小到大
3. 当然也可以手写cmp，传入cmp。

AC代码：

 

#include<iostream>
#include<cstdlib>
#include<cstring>
#include<vector>
#include<algorithm>
using namespace std;
vector<int>a[100010];
int cmp(const int a,const int b){
    return a>b;
}
int sum[100010];
int main()
{
    int n,m;
    while (cin>>n>>m){
        vector <int>::iterator it;
        int x,y;
        memset(sum,0,sizeof(sum));
        for (int i=0;i<n;i++){
            cin>>x>>y;
            a[x].push_back(y);
        }
        for (int i=1;i<=n;i++){
            sort(a[i].begin(),a[i].end(),cmp);
        }
        for (int i=1;i<=m;i++){
            for (int j=1;j<a[i].size();j++){
                a[i][j]+=a[i][j-1];
            }
        }
        int ans=0;
        for (int i=1;i<=m;i++){
            for (int j=0;j<a[i].size();j++){
                if (a[i][j]>0){
                    sum[j]+=a[i][j];
//                printf("sum[%d]=%d\n",j,sum[j]);
                ans=max(ans,sum[j]);
                }
            }
            a[i].clear();
        }
        printf("%d\n",ans);
    }
    return 0;
}