生成树（构造）
NOIP 模拟赛的题目，先贴上题面。
题目描述
我们知道，生成树是图 \(G\) 的一个子集，它的所有顶点都被尽可能少的边覆盖。因此，生成树没有环，也不能是多个联通块。
显然，我们知道一个图的生成树是不唯一的。
给定一个任意的无向简单图（没有重边和自环），我们现在定义生成树去除：找到该图的任意一棵生成树，并从原始图中去除生成树包含的所有边，得到一个新图。
Cuber QQ 发现“生成树去除”非常有趣，以至于他想一遍又一遍地做。
显然，他想从一个完全图（每对不同的顶点都通过唯一的边连接的图）开始。通过巧妙的选择要移除的生成树，以便可以重复移除尽可能多的次数，直到图中不再有生成树。
输入格式
输入第一行包含一个整数 \(T\)，表示测试数据的数量。
每组测试数据包含一行，一个整数 \(n\) 表示完全图的点数。
输出格式
对于每个测试用例，输出第一行包含 Case #x: y，其中 \(x\) 是从 \(1\) 开始的测试用例编号，\(y\) 是最多可以进行删除的次数。
接下来的 \(y\times (n-1)\) 行，从 \((n-1)\times (i+1)+1\) 行到 \((n-1)\times i\) 行，输出你第 \(i\) 次决定删除的生成树。每行包含两个数字 \(u\) 和 \(v(1\le u,v\le n,u\ne v)\)，\((u,v)\) 应该是有效的树边，并且与之前被移除的边不重合。
如果有多个解，输出其中任何一个。
数据范围
对于 \(20\%\) 的数据，\(n\le 20\)。
对于 \(50\%\) 的数据，\(n\le 50\)。
对于 \(100\%\) 的数据，\(1\le T\le 500,2\le n\le 1000,\sum n\le 1000\)。
解题思路
“删除次数”可以看作提示——手玩样例发现，\(n=2\) 或 \(n=3\) 时，删除次数为 \(1\)；\(n=4\) 或 \(n=5\) 时，删除次数为 \(2\)，\(n=6\) 或 \(n=7\) 时，删除次数为 \(3\)。我们猜测，对于 \(n\) 个点的完全图（\(n\) 为偶数），删除次数为 \(\frac{n}{2}\)，而奇数点的情况可以减一转化为偶数点的情况。
对于偶数点的情况，考虑怎样构造方案。满足既不能成环，又能连通的方案不唯一，这里给出其中一种：将有 \(n\) 个点的完全图画成一个圆，从前 \(\frac{n}{2}\) 个点出发，“反复横跳”，即向右一步、向左两步、向右三步、向左四步……如下图所示：
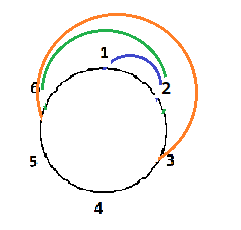
以从 \(1\) 开始为例，\(1\to 2 \to 6 \to 3 \to 5 \cdots\)。这样连出的生成树是一条链：
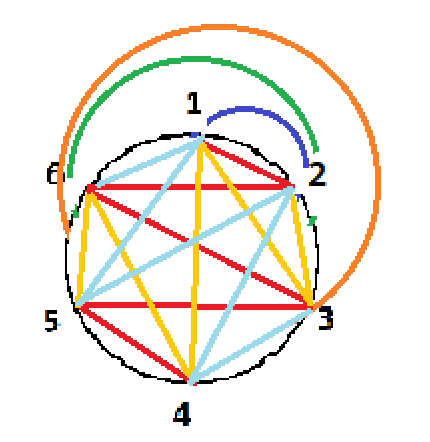
mspaint 比较糊……至此，我们解决了偶数点的问题，考虑怎样将奇数点转化为偶数点。可以认为奇数点就是在上图的基础上增加了一个 \(n+1\) 号点，我们只需将前 \(\frac{n}{2}\) 个点分别向 \(n+1\) 号点连一条边即可。
代码实现
直接上代码（很短）；
void main() {//包在namespace里才这么写的
int T;
scanf("%d",&T);
for(int test(1); test<=T; ++test) {
int n;
bool odd=false;
scanf("%d",&n);
printf("Case #%d: %d\n",test,n>>1);
if(n&1) --n,odd=true;//直接转化为偶数情况
for(int i=0; i<(n>>1); ++i) {
int x=i,d=1,f=1;//d是每一步的大小，f控制往左还是往右走，因为是环，所以越界时可以直接mod n
while(d<n) {
printf("%d %d\n",x+1,(x+d*f+n)%n+1);//避免mod时出现0
x+=d*f,x=(x+n)%n,++d,f=-f;
}
if(odd) printf("%d %d\n",i+1,n+1);//若为奇数，则与n+1号点连边
}
}
}
