可持久化线段树学习笔记

可持久化数据结构对空间有要求，其优点是充分利用了已经“记住”的信息。

一、 可持久化数组

P3919 【模板】可持久化线段树 1（可持久化数组）中这样说：

“如题，你需要维护这样的一个长度为 \(N\) 的数组，支持如下几种操作

1. 在某个历史版本上修改某一个位置上的值;

2. 访问某个历史版本上的某一位置的值.

此外，每进行一次操作（对于操作2，即为生成一个完全一样的版本，不作任何改动），就会生成一个新的版本。版本编号即为当前操作的编号（从1开始编号，版本0表示初始状态数组）。

“一个完全一样的版本”，首先想到的是——全部记下来，也就是每一次更新，都把数组做一次 memcpy() 操作。这样做的代价，不提复制所用的时间，空间复杂度也会增长至 \(O(nm)\) 量级，陷入MLE的深渊里无法自拔。

However, 为什么要全复制一遍呢？一个显然的方法是，只把改变的点复制出来，或者说，对于改变的的节点，在运算时动态创建一个新的，保留原来的作为历史版本。 这样，空间复杂度（以线段树为例，每次修改 \(log_n\) 个点）就只有 \(O(n*4+q*log_n)\) 了。

在代码实现的时候，我们实际上建立起了 \(q\) 棵线段树，但是对于没有修改的儿子，直接把指针指向左边那棵线段树对应的位置——这样建立起来的线段树，一般来说，只有最开始的那棵是完整的，而右侧的都是有独立的根、但依附连接于其上的附着物。

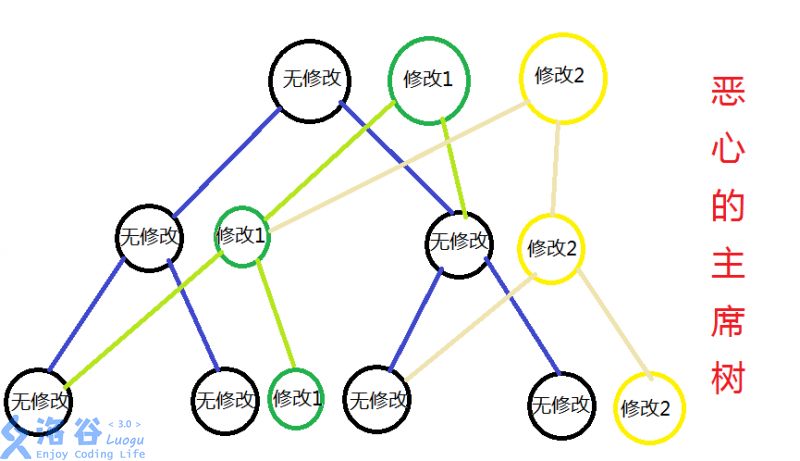
二、 静态区间第k小

看到第k小的字样，一下子想起平衡树。主席树有时确实能实现与平衡树相似的功能，但她们的本质却是大相径庭。

P3834 【模板】可持久化线段树 2（主席树）里这样描述：

“如题，给定 \(n\) 个整数构成的序列 \(a\) ，将对于指定的闭区间 \([l,r]\) 查询其区间内的第 \(k\) 小值。”

我们建立一棵主席树，他维护的是“值域”，即所谓权值线段树。每读入一个数，就做一次 update() 以加入，留下了 \(n\) 个版本。线段树 \(i\) 每个点的 \(t[p].val\) 值为 \([1,i]\) 范围内，\([t[p].l,t[p].r]\) 内有多少个不同的数字。按照前缀和方式计算出 \(x\) 与 \(mid\) 相比较，并确定向左还是右递归。

下面是代码。要特别注意，对于右子树的 update() 操作，第二个参数传的是 \(k-x\) 。这与 \(Splay\) 中求 \(kth\) 的方法十分相近。

#include<stdio.h>
#include<algorithm>
const int N=2e5+10;
struct ZldTree{int ls,rs,val;}t[N<<5];
int n,q,m,tot,a[N],b[N],root[N];
inline int rd(){
	int x=0,f=1;char c=getchar();
	while(c<'0'||c>'9'){if(c=='-') f^=1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
	return f?x:-x;
}
inline int New(int p){
	t[++tot]=t[p];
	++t[tot].val;
	return tot;
}
int build(int l,int r){
	int p=++tot;
	if(l==r) return p;
	int mid=(l+r)>>1;
	t[p].ls=build(l,mid);
	t[p].rs=build(mid+1,r);
	return p;
} 
int update(int p,int l,int r,int x){
	p=New(p);
	if(l==r) return p;
	int mid=(l+r)>>1;
	if(x<=mid) t[p].ls=update(t[p].ls,l,mid,x);
	else t[p].rs=update(t[p].rs,mid+1,r,x);
	return p;
}
int query(int u,int v,int l,int r,int k){
	if(l>=r) return l;
	int x=t[t[v].ls].val-t[t[u].ls].val;
	int mid=(l+r)>>1;
	if(x>=k) return query(t[u].ls,t[v].ls,l,mid,k);
	else return query(t[u].rs,t[v].rs,mid+1,r,k-x);
}
int main(){
	n=rd(),q=rd();
	for(int i=1;i<=n;++i) a[i]=b[i]=rd();
	std::sort(b+1,b+n+1);
	m=std::unique(b+1,b+n+1)-b-1;
	root[0]=build(1,m);
	for(int i=1;i<=n;++i){
		a[i]=std::lower_bound(b+1,b+m+1,a[i])-b;
		root[i]=update(root[i-1],1,m,a[i]);
	}
	while(q--){
		int l=rd(),r=rd(),k=rd();
		printf("%d\n",b[query(root[l-1],root[r],1,m,k)]);
	}
	return 0;
} 

三、 可持久化并查集

模板题是P3402 可持久化并查集。

世界上根本没有所谓“可持久化”的并查集，有的只是用主席树模拟的并查集。这与前面两部分一脉相承。

题目要求：

“给定 \(n\) 个集合，第 \(i\) 个集合内初始状态下只有一个数，为 \(i\) 。

有 \(m\) 次操作。操作分为 \(3\) 种：

1 a b 合并 \(a,b\) 所在集合；

2 k 回到第 \(k\) 次操作（执行三种操作中的任意一种都记为一次操作）之后的状态；

3 a b 询问 \(a,b\) 是否属于同一集合，如果是则输出 \(1\) ，否则输出 \(0\) 。”

考虑用主席树维护每个并查集里每个节点的父亲关系。平时写的一行并查集 inline int find(int x){return x==fa[x]?x:fa[x]=find(fa[x]);} 运用了路径压缩算法，大大减小了时间消耗。但是，路径压缩的并查集不利于可持久化。为了方便模拟，可持久化的并查集不路径压缩。

在寻找 \(father\) 时，我们要做的就是在主席树上找到点 \(u=find(a)\) 和 \(v=find(b)\) ，分别向上跑直到 \(root\) ，然后把前者的父亲设为后者，像普通版一样。

不路径压缩……似乎还有问题：就像BST的退化，并查集也可能退化为一条长链，时间复杂度再次崩溃。为了解决这一问题，我们采取启发式合并，即把最大深度最小的连通块往最大深度大的上面合并。证明。

思考：代码中为什么 update(root[i],t[u].fa,t[v].fa) ？

代码如下：

#include<stdio.h>
const int N=2e5+10;
struct ZldTree{int l,r,lson,rson,fa,dep;}t[N<<4];
#define ls t[p].lson
#define rs t[p].rson
#define mid ((t[p].l+t[p].r)>>1)
int n,m,tot,root[N];
inline int rd(){
	int x=0,f=1;char c=getchar();
	while(c<'0'||c>'9'){if(c=='-') f^=1;c=getchar();}
	while(c>='0'&&c<='9'){x=(x<<1)+(x<<3)+(c^48);c=getchar();}
	return f?x:-x;
}
inline void swap(int &x,int &y){x^=y^=x^=y;}
inline int New(int p){
	t[++tot]=t[p];
	return tot;
}
int build(int l,int r){
	int p=++tot; 
	t[p].l=l,t[p].r=r;
	if(l==r){t[p].fa=l;return p;}
	t[p].lson=build(l,mid);
	t[p].rson=build(mid+1,r);
	return p;
}
int update(int p,int u,int v){
	p=New(p);
	int l=t[p].l,r=t[p].r;
	if(l==r){t[p].fa=v;return p;}
	if(u<=mid) t[p].lson=update(ls,u,v);
	else t[p].rson=update(rs,u,v);
	return p;
}
int query(int p,int x){
	int l=t[p].l,r=t[p].r;
	if(l==r) return p;
	if(x<=mid) return query(ls,x);
	else return query(rs,x);
}
void add(int p,int x){
	int l=t[p].l,r=t[p].r;
	if(l==r){++t[p].dep;return;}
	if(x<=mid) add(ls,x);
	else add(rs,x);
}
int find(int rt,int x){
	int v=query(root[rt],x);
	if(t[v].fa==x) return v;
	return find(rt,t[v].fa);
}
int main(){
	n=rd(),m=rd();
	root[0]=build(1,n);
	for(int i=1,opt,k,a,b;i<=m;++i){
		opt=rd();
		root[i]=root[i-1]; 
		if(opt==1){
			a=rd(),b=rd();
			int u=find(i,a),v=find(i,b);
			if(t[u].fa==t[v].fa) continue;
			if(t[u].dep>t[v].dep) swap(u,v);
			root[i]=update(root[i],t[u].fa,t[v].fa);
			if(t[u].dep==t[v].dep) add(root[i],t[v].fa);
		}
		else if(opt==2){
			k=rd();
			root[i]=root[k];
		}
		else{
			a=rd(),b=rd();
			int u=find(i,a),v=find(i,b);
			if(u==v) putchar('1');
			else putchar('0');
			putchar('\n');
		}
	}
	return 0;
}

THE END