二分类问题中的混淆矩阵、ROC以及AUC评估指标
本篇博文简要讨论机器学习二分类问题中的混淆矩阵、ROC以及AUC评估指标;作为评价模型的重要参考,三者在模型选择以及评估中起着指导性作用。
按照循序渐进的原则,依次讨论混淆矩阵、ROC和AUC:
设定一个机器学习问题情境:给定一些肿瘤患者样本,构建一个分类模型来预测肿瘤是良性还是恶性,显然这是一个二分类问题。
当分类模型选定以后,将其在测试数据集上进行评估,分别可以得到以下评估指标:
混淆矩阵
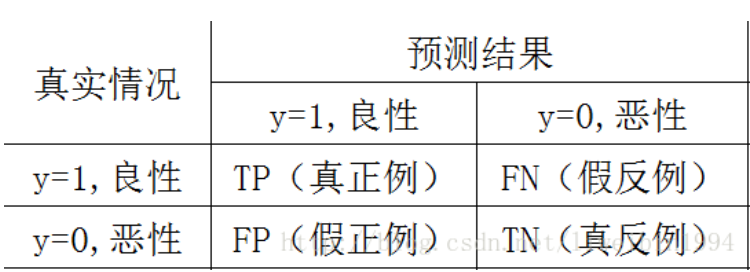
TP表示预测为良性,真实情况是良性的样例数;
FN表示预测为恶性,真实情况是良性的样例数;
FP表示预测为良性,真实情况是恶性的样例数;
TN表示预测为恶性,真实情况是恶性的样例数;
以上四类数据构成混淆矩阵。
ROC曲线
在混淆矩阵的基础上,进一步地定义两个参数。
按照下式定义FPR参数
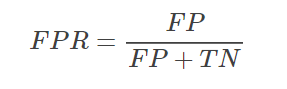
FPR表示,在所有的恶性肿瘤中,被预测成良性的比例。称为伪阳性率。伪阳性率告诉我们,随机拿一个恶性的肿瘤样本,有多大概率会将其预测成良性肿瘤。显然FPR越小越好。
按照下式定义TPR参数

TPR表示,在所有良性肿瘤中,被预测为良性的比例。称为真阳性率。真阳性率告诉我们,随机拿一个良性的肿瘤样本时,有多大概率会将其预测为良性肿瘤。显然TPR越大越好。
由上,一个混淆矩阵对应一对(FPR,TPR)
需要明确的是,FPR和TPR是建立在类别明确的预测结果之上的,即分类模型明确地指出待预测样本的类别。
然而,在二分类问题(0,1)中,一般模型最后的输出是一个概率值,表示结果是1的概率。此时需要确定一个阈值,若模型的输出概率超过阈值,则归类为1;若模型的输出概率低于阈值,则归类为0。
不同的阈值会导致分类的结果不同,也就是混淆矩阵有差,FPR和TPR也就不同。
当阈值从0开始慢慢移动到1的过程,就会形成很多对(FPR, TPR)的值,将它们画在坐标系上,就是所谓的ROC曲线了。
AUC
得到ROC曲线后,就可以计算曲线下方的面积,计算出来的面积就是AUC值。
一般而言,AUC越大,模型的性能越好。
示例
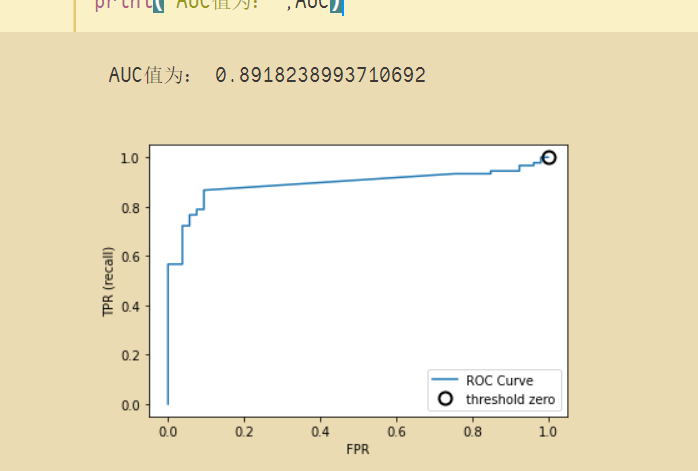
作者: pythonfl
出处: http://www.cnblogs.com/pythonfl/
本文版权归作者和博客园共有,转载时请标明出处;如有疑问,欢迎联系fangleiecust@163.com;如发现文中内容侵犯到您的权利,请联系作者予以处理。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号