Python数据可视化的10种技能
今天我来给你讲讲Python的可视化技术。
可视化视图都有哪些?
按照数据之间的关系,我们可以把可视化视图划分为4类,它们分别是比较、联系、构成和分布。我来简单介绍下这四种关系的特点:
比较:比较数据间各类别的关系,或者是它们随着时间的变化趋势,比如折线图;
联系:查看两个或两个以上变量之间的关系,比如散点图;
构成:每个部分占整体的百分比,或者是随着时间的百分比变化,比如饼图;
分布:关注单个变量,或者多个变量的分布情况,比如直方图。
同样,按照变量的个数,我们可以把可视化视图划分为单变量分析和多变量分析。
-
单变量分析指的是一次只关注一个变量。比如我们只关注“身高”这个变量,来看身高的取值分布,而暂时忽略其他变量。
-
多变量分析可以让你在一张图上可以查看两个以上变量的关系。比如“身高”和“年龄”,你可以理解是同一个人的两个参数,这样在同一张图中可以看到每个人的“身高”和“年龄”的取值,从而分析出来这两个变量之间是否存在某种联系。
可视化的视图可以说是分门别类,多种多样,今天我主要介绍常用的10种视图,包括了散点图、折线图、直方图、条形图、箱线图、饼图、热力图、蜘蛛图、二元变量分布、成对关系。
散点图
散点图的英文叫做scatter plot,它将两个变量的值显示在二维坐标中,非常适合展示两个变量之间的关系。当然,除了二维的散点图,我们还有三维的散点图。
我在上一讲中给你简单介绍了下Matplotlib这个工具,在Matplotlib中,我们经常会用到pyplot这个工具包,它包括了很多绘图函数,类似Matlab的绘图框架。在使用前你需要进行引用:
import matplotlib.pyplot as plt
在工具包引用后,画散点图,需要使用plt.scatter(x, y, marker=None)函数。x、y 是坐标,marker代表了标记的符号。比如“x”、“>”或者“o”。选择不同的marker,呈现出来的符号样式也会不同,你可以自己试一下。
下面三张图分别对应“x”“>”和“o”。



除了Matplotlib外,你也可以使用Seaborn进行散点图的绘制。在使用Seaborn前,也需要进行包引用:
import seaborn as sns
在引用seaborn工具包之后,就可以使用seaborn工具包的函数了。如果想要做散点图,可以直接使用sns.jointplot(x, y, data=None, kind='scatter')函数。其中x、y是data中的下标。data就是我们要传入的数据,一般是DataFrame类型。kind这类我们取scatter,代表散点的意思。当然kind还可以取其他值,这个我在后面的视图中会讲到,不同的kind代表不同的视图绘制方式。
好了,让我们来模拟下,假设我们的数据是随机的1000个点。
# 数据准备
N = 1000
x = np.random.randn(N)
y = np.random.randn(N)
# 用Matplotlib画散点图
plt.scatter(x, y,marker='x')
plt.show()
# 用Seaborn画散点图
df = pd.DataFrame({'x': x, 'y': y})
sns.jointplot(x="x", y="y", data=df, kind='scatter');
plt.show()
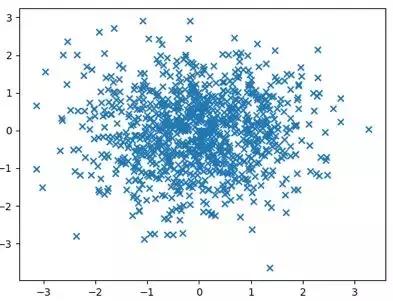
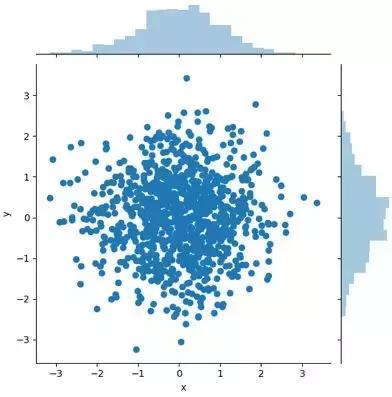
我们运行一下这个代码,就可以看到下面的视图(第一张图为Matplotlib绘制的,第二张图为Seaborn绘制的)。其实你能看到Matplotlib和Seaborn的视图呈现还是有差别的。Matplotlib默认情况下呈现出来的是个长方形。而Seaborn呈现的是个正方形,而且不仅显示出了散点图,还给了这两个变量的分布情况。
Matplotlib绘制:
Seaborn绘制:
折线图
折线图可以用来表示数据随着时间变化的趋势。
在Matplotlib中,我们可以直接使用plt.plot()函数,当然需要提前把数据按照X轴的大小进行排序,要不画出来的折线图就无法按照X轴递增的顺序展示。
在Seaborn中,我们使用sns.lineplot (x, y, data=None)函数。其中x、y是data中的下标。data就是我们要传入的数据,一般是DataFrame类型。
这里我们设置了x、y的数组。x数组代表时间(年),y数组我们随便设置几个取值。下面是详细的代码。
# 数据准备
x = [2010, 2011, 2012, 2013, 2014, 2015, 2016, 2017, 2018, 2019]
y = [5, 3, 6, 20, 17, 16, 19, 30, 32, 35]
# 使用Matplotlib画折线图
plt.plot(x, y)
plt.show()
# 使用Seaborn画折线图
df = pd.DataFrame({'x': x, 'y': y})
sns.lineplot(x="x", y="y", data=df)
plt.show()
然后我们分别用Matplotlib和Seaborn进行画图,可以得到下面的图示。你可以看出这两个图示的结果是完全一样的,只是在seaborn中标记了x和y轴的含义。
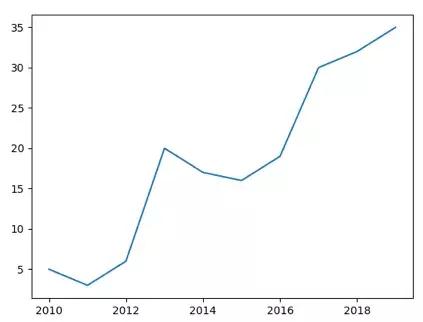
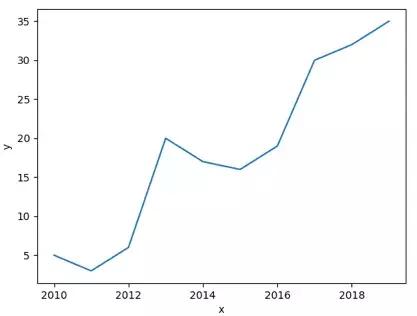
直方图
直方图是比较常见的视图,它是把横坐标等分成了一定数量的小区间,这个小区间也叫作“箱子”,然后在每个“箱子”内用矩形条(bars)展示该箱子的箱子数(也就是y值),这样就完成了对数据集的直方图分布的可视化。
在Matplotlib中,我们使用plt.hist(x, bins=10)函数,其中参数x是一维数组,bins代表直方图中的箱子数量,默认是10。
在Seaborn中,我们使用sns.distplot(x, bins=10, kde=True)函数。其中参数x是一维数组,bins代表直方图中的箱子数量,kde代表显示核密度估计,默认是True,我们也可以把kde设置为False,不进行显示。核密度估计是通过核函数帮我们来估计概率密度的方法。
这是一段绘制直方图的代码。
# 数据准备
a = np.random.randn(100)
s = pd.Series(a)
# 用Matplotlib画直方图
plt.hist(s)
plt.show()
# 用Seaborn画直方图
sns.distplot(s, kde=False)
plt.show()
sns.distplot(s, kde=True)
plt.show()
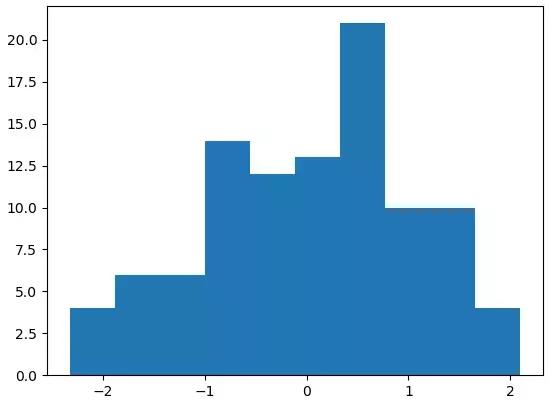
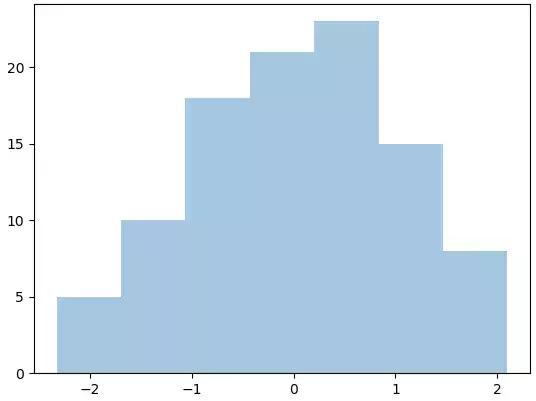
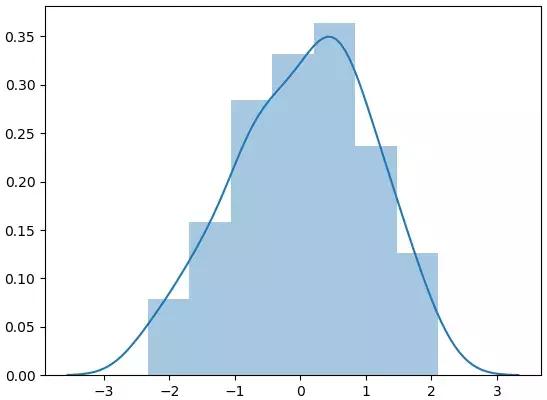
我们创建一个随机的一维数组,然后分别用Matplotlib和Seaborn进行直方图的显示,结果如下,你可以看出,没有任何差别,其中最后一张图就是kde默认为Ture时的显示情况。
热力图
热力图,英文叫heat map,是一种矩阵表示方法,其中矩阵中的元素值用颜色来代表,不同的颜色代表不同大小的值。通过颜色就能直观地知道某个位置上数值的大小。另外你也可以将这个位置上的颜色,与数据集中的其他位置颜色进行比较。
热力图是一种非常直观的多元变量分析方法。
我们一般使用Seaborn中的sns.heatmap(data)函数,其中data代表需要绘制的热力图数据。
这里我们使用Seaborn中自带的数据集flights,该数据集记录了1949年到1960年期间,每个月的航班乘客的数量。
# 数据准备
flights = sns.load_dataset("flights")
data=flights.pivot('year','month','passengers')
# 用Seaborn画热力图
sns.heatmap(data)
plt.show()
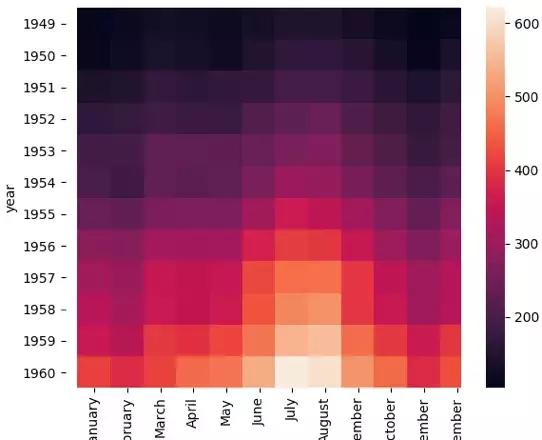
通过seaborn的heatmap函数,我们可以观察到不同年份,不同月份的乘客数量变化情况,其中颜色越浅的代表乘客数量越多,如下图所示:
成对关系
如果想要探索数据集中的多个成对双变量的分布,可以直接采用sns.pairplot()函数。它会同时展示出DataFrame中每对变量的关系,另外在对角线上,你能看到每个变量自身作为单变量的分布情况。它可以说是探索性分析中的常用函数,可以很快帮我们理解变量对之间的关系。
pairplot函数的使用,就好像我们对DataFrame使用describe()函数一样方便,是数据探索中的常用函数。
这里我们使用Seaborn中自带的iris数据集,这个数据集也叫鸢尾花数据集。鸢尾花可以分成Setosa、Versicolour和Virginica三个品种,在这个数据集中,针对每一个品种,都有50个数据,每个数据中包括了4个属性,分别是花萼长度、花萼宽度、花瓣长度和花瓣宽度。通过这些数据,需要你来预测鸢尾花卉属于三个品种中的哪一种。
# 数据准备
iris = sns.load_dataset('iris')
# 用Seaborn画成对关系
sns.pairplot(iris)
plt.show()
这里我们用seaborn中的pairplot函数来对数据集中的多个双变量的关系进行探索,如下图所示。从图上你能看出,一共有sepal_length、sepal_width、petal_length和petal_width4个变量,它们分别是花萼长度、花萼宽度、花瓣长度和花瓣宽度。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号