4.无监督学习--K-means聚类
K-means方法及其应用
1.K-means聚类算法简介:
k-means算法以k为参数,把n个对象分成k个簇,使簇内具有较高的相似度,而簇间的相似度较低。主要处理过程包括:
1.随机选择k个点作为初始的聚类中心。
2.对于剩下的点,根据其与聚类中心的距离,将其归入最近的簇。
3.对每个簇,计算所有点的均值作为新的聚类中心。
4.重复2、3直到聚类中心不再发生改变。
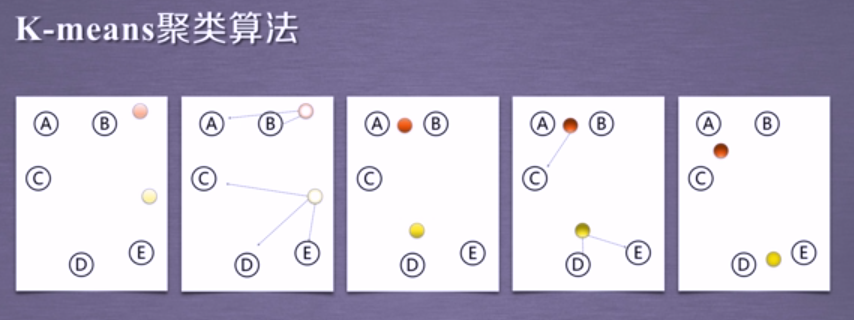
举例:对于A、B、C、D、E这5个点,我们先随机选择两个点作为簇中心点,标记为红色和黄色,对于第一次聚类结果,我们分别计算所有的点到这两个中心点之间的聚类,我们发现A、B亮点离红色的点距离更近,、C、D、E三点离黄色的点距离更近,所以在第一次聚类过程中,这个簇被定义为:A、B为一个簇,C、D、E为一个簇,接下来,我们将A、B这个簇重新计算它的聚类中心,标记为一个更深颜色的红色的点,C、D、E重新计算他们的簇中心,为一个更深颜色的黄色的点,我们再重新计算这些所有点距离簇中心的距离,接下来我们可以发现,A、B、C可以聚为一个簇,而D、E相对于黄色的簇中心距离更近,所以D、E为一个簇,因此我们再重新计算一下A、B、C这个簇的簇中心和D、E的簇中心,第5张图我们就可以看到簇的组成已经相对稳定了,那么这5个点的聚类结果就是:A、B、C为一个簇,D、E为一个簇,红色和黄色的点分别为这两个簇的簇中心;演变过程如下:
2.K-means的应用
1.数据介绍:
现有1999年全国31个省份城镇居民家庭平均每人全年消费性支出的八个主要变量数据,这8个变量分别是:食品、衣着、家庭设备用品及服务、医疗保健、交通和通讯、 娱乐教育文化服务、居住以及杂项商品和服务。利用已有数据,对31个省份进行聚类。
2.实验目的:
通过聚类,了解1999年各个省份的消费水平在国内的情况。
3.技术路线:sklearn.cluster.Kmeans
4.数据实例展示:
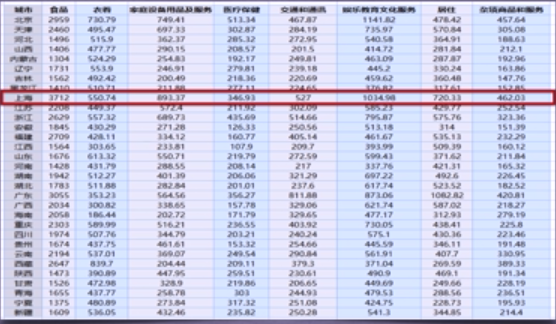
1999年全国31个省份城镇居民家庭平均每人全年消费性支出数据,如下所示:
5.实验过程:
1.使用算法:K-means聚类算法
2.实现过程:
1.建立工程,导入sklearn相关包
import numpy as np
from sklearn.cluster import KMeans
2.加载数据,创建K-means算法实例,并进行训练,获得标签:

注意:调用K-Means方法所需参数:
1.n_clusters:用于指定聚类中心的个数
2.init:初始聚类中心的初始化方法
3.max_iter:最大的迭代次数
4.一般调用时只用给出n_clusters即可,init默认是k-means++,max_iter默认是300。
其它参数:
1.data:加载的数据
2.label:聚类后各数据所属的标签
3.fit_predict():计算簇中心以及为簇分配序号
重点方法解释:
data,cityName = loadData('city.txt') #loadData()函数是我们自己定义的,具体代码为:

def loadData(filePath): fr = open(filePath,'r+') #r+:读写方式打开一个文本文件 lines = fr.readlines() retData = [] retCityName = [] for line in lines: items = line.strip().split(",") retCityName.append(items[0]) retData.append(float(items[1])) for i in range(1,len(items)): return retData,retCityName
注意:loadData()函数中的readlines()方法一次性读取整个文件,类似于.read()
retCityName用于存储城市名称;
retData 用于存储城市的各项消费信息
返回值:返回城市名称以及该城市的各项消费信息
展示的时候:

3.输出标签,查看结果
1.我们将城市按照消费水平n_clusters分为几个类,消费水平相近的城市聚集在一类中。
2.expenses:聚类中心店的数值加和,也就是平均消费水平。
如下展示了:当n_clusters=2时,消费水平的聚类结果,聚成2类,我们可以看到其中一类是:北京、天津、上海、浙江、福建、广东、重庆、西藏为一个消费水平的;

当n_clusters=3或者n_clusters=4的时候的聚类情况如下所示:

从这些结果中我们可以看出,消费水平相近的城市聚集在一个类中,而北京、上海、广东很稳定的一直聚集在了同一个类中!
如下,我们简单谈一下sklearn库中的k-means算法的拓展和改进;
3.拓展 && 改进
计算两条数据相似性时,Sklearn的K-Means默认用的是欧氏距离。虽然还有余弦相似度,马氏距离等多种方法,但sklearn中的k-means算法没有设定计算距离方法的参数。如果大家想要使用自定义计算距离的计算方法,那么我们可以更改k-means的源代码,在这里我们建议使用scipy.spatial.distance.cdist方法。

当设置metric="cosine"的时候,就相当于我们要使用余弦距离了,使用形式:scipy.spatial.distance.cdist(A,B,metric="cosine")




 浙公网安备 33010602011771号
浙公网安备 33010602011771号